உலகின் நேரமண்டலங்கள்

உலகின் நேரமண்டலங்கள் (World Time Zones)

இடைக்கால மனிதர்கள் சூரியக்கடிகாரங்கள் மற்றும் நீர்கடிகாரங்களைக் கொண்டு சூரியன் தீர்க்கரேகையை கடப்பதை கண்காணித்தனர். 17ஆம் நூற்றாண்டில், மனிதர்கள் ஊசல் கடிகாரங்களைப் பயன்படுத்த ஆரம்பித்தனர். இது கடலில் செல்லும் போது சரியான நேரத்தை காட்டுவதில்லை. பின்னாளில் காலக்கடிகாரம் (1764 இல்) கண்டுபிடிக்கப்பட்டது. இக்காலக்கடிகாரம் நேரத்தை துல்லியமாக காட்டக்கூடியது. கப்பலோட்டிகள் 19 ஆம் நூற்றாண்டில் இதை அதிக அளவில் பயன்படுத்தினர். ஆனால் பெரும்பாலான சிறுநகரங்கள் மற்றும் பெருநகரங்களில் கடிகாரங்கள் சூரிய உதயம் மற்றும் சூரிய மறைவை வைத்தே கணிக்கப்பட்டது. இப்படி உருவாக்கப்பட்ட உள்ளூர் சூரிய கடிகாரங்கள் இரயில் போக்குவரத்து மற்றும் தொலைதொடர்பு சாதனங்களின் வளர்ச்சிக்குத் தடையாக இருந்தது. நேர மண்டலம் என்பது புவியின் ஒரு பகுதியில் போக்குவரத்து வியாபாரம் மற்றும் சமுதாய நலன்களுக்காக ஒரே சீராக நிலையான நேரத்தை பராமரிப்பது ஆகும். உதாரணமாக, வெவ்வேறு நேர மண்டலம் பின்பற்றப்பட்டால் வெவ்வேறு பகுதிகளில் இருந்துவரும் இரயில்கள் ஒரே இரயில்பதையில் வந்து விபத்துக்கு ஆளாக நேரிடும்.

தீர்க்கரேகை மற்றும் சுற்றும் புவியை தொடர்புபடுத்தி உலகின் நேர மண்டலங்கள் (படம் எண் 2.17) உருவாக்கப்பட்டது. முதன்மை (0o) தீர்க்க ரேகையே நேரமண்டலத்திற்கு மையமாகும். இது 7 ½o மேற்கு மற்றும் 7 ½° கிழக்கு தீர்க்கரேகையிலிருந்து நீட்டிக்கப்பட்டுள்ளது. அனைத்து நேரமண்டலங்களும் கிரீன்விச் மத்திய நேரத்தை பின்பற்றும் படியாக 24 மணி நேரங்களை கொண்ட நேரமண்டலமாக உருவாக்கப்பட்டுள்ளன. புவி 24 நேர மண்டலங்களாக பிரிக்கப்பட்டுள்ளது. ஒவ்வொரு மண்டலமும் ஒருமணி நேரத்தைக் குறிக்கும். ஏனென்றால் புவியானது ஒருமணி நேரத்தில் 15 தீர்க்கரேகையை கடக்கிறது (360" / 24 மணிநேரம்). சூரியன் முதன்மை தீர்க்க ரேகையில் வரும் போது 7 ½o மேற்கு மற்றும் 7 ½o கிழக்கு இடையில் உள்ள அனைத்துப் பகுதிகளும் நண்பகலாக கருதப்படுகிறது.

பகல் சேமிப்பு நேரம்

மத்திய அட்சரேகையில் காணப்படும் ஐரோப்பா, வட அமெரிக்கா, ஆஸ்திரேலியா மற்றும் தென் அமெரிக்கா ஆகிய நாடுகளில் கோடைகாலங்களில் பகல் நேரம் இரவு நேரத்தை விட கூடுதலாக இருக்கும். பகல் நேர கால அளவை செயல்படுத்திய போதும் பகல் நேரத்தை வசந்த காலங்களில் ஒருமணி நேரம் முன்பாகவும் இலையுதிர் காலங்களில் ஒருமணி நேரம் பின்பாகவும் சரி செய்யப்படுகிறது. இது பொதுவாக பகல் சேமிப்பு நேரம் (Daylight Saving Time) என அறியப்படுகிறது

நேர மண்டலங்கள் (Time Zones)

புவியானது தன் அச்சில் 360° யை ஒவ்வொரு 24 மணி நேரத்திற்கும் ஒருமுறை சுற்றிவருகிறது. புவி தன் ஒரு சுற்றை முடிக்க ஒருநாள் எடுத்துக் கொள்வதை நீங்கள் காணலாம். நேர விகிதத்தின் படி ஒரு மணி நேரத்தில் 15° கடக்கிறது. (360°/24) சுற்றுவதைக் காணலாம் (360°/24). இந்த எண் நேர மண்டலங்களை நிர்ணயிப்பதில் ஒரு முக்கிய பங்கு வகிக்கிறது. நீங்கள், ஏற்கனவே உங்கள் கீழ்வகுப்புகளில் அட்சரேகை மற்றும் தீர்க்கரேகை அவற்றின் பயன்கள் குறித்து படித்திருப்பீர்கள்.

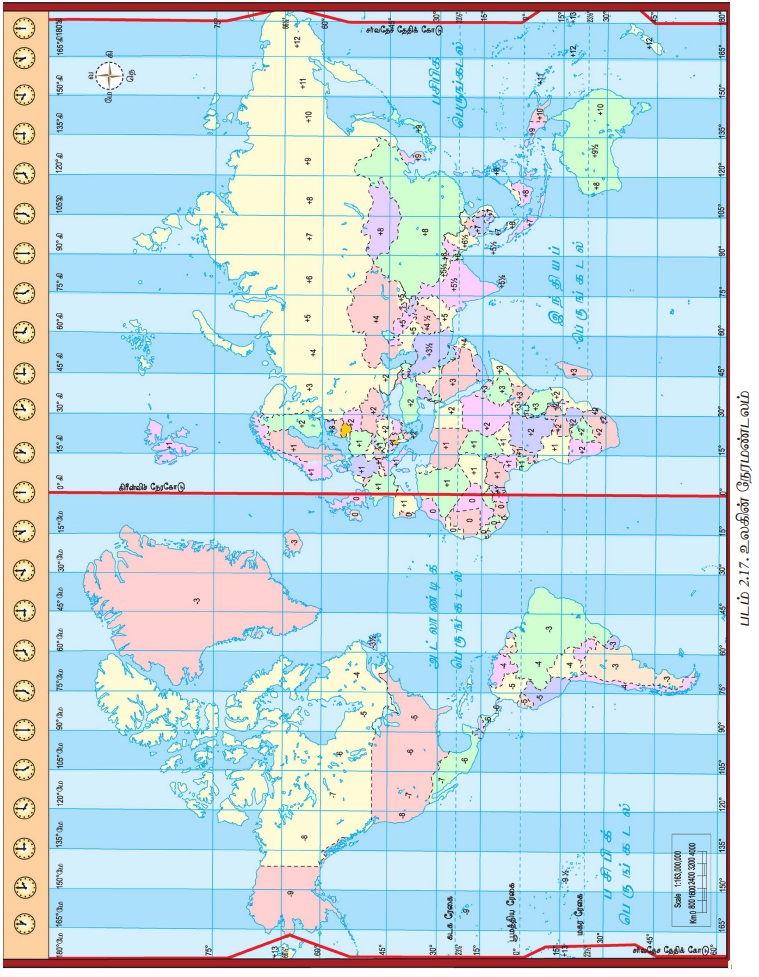
நேரமண்டலங்களை நிர்ணயிப்பதில் அட்சரேகைகள் மற்றும் தீர்க்கரேகைகள் முக்கிய பங்கு வகிக்கின்றன. இவைகள் புவியைப் பிரிக்கும் கற்பனைக் கோடுகளாகும். அட்சரேகை என்பது புவியைச் சுற்றி கிழக்கு மேற்காக செல்லும். அவை வடதுருவம் மற்றும் தென் துருவத்தில் உள்ள இடங்களை அளக்க உதவும். இக்கோடுகள் நிலநடுக்கோட்டிலிருந்து ஆரம்பித்து 0 லிருந்து 90° வரை வடக்காகவும் மேலும் 0° யிலிருந்து 90° வரை தெற்காகவும் செல்லும். இவைகள் நிலநடுக்கோட்டிலிருந்து தொலைவில் செல்லச்செல்ல சிறியதாகின்றன. ஆனால் தீர்க்கரேகைகள் வடக்கு தெற்காக வரையப்படுகின்றன. அவைகள் மேற்கு கிழக்கு துருவங்களில் உள்ள பகுதிகளை அளக்கின்றன. இவை முதன்மை தீர்க்கரேகையில் ஆரம்பித்து 0° லிருந்து 180° வரை கிழக்காகவும் மேலும் 0° லிருந்து 180° மேற்காகவும் செல்கின்றன. அட்சரேகைகள் போல இல்லாமல் இவை சமநீள கோடுகளாகும். இந்த கோள ஒருங்கிணைப்பு திட்டம் 0° தீர்க்கரேகையிலும் 0° அட்சரேகையிலும் அமைந்துள்ளது. இந்தப்புள்ளி அட்லாண்டிக் பெருங்கடல் பகுதியில் உள்ள தென்மேற்கு ஆப்பிரிக்காவிற்கு அருகில் காணப்படுகிறது. மேலும் இந்த இரண்டு கோடுகளும் 180° அல்லது சர்வதேச தேதி கோட்டில் சந்திக்கின்றன. இது உலகில் வெவ்வேறு நேரமண்டலங்களை நிர்ணயிக்க உதவுகிறது.

மேற்கண்ட அனைத்து தகவல்களும் இரண்டு அமைவிடங்களுக்கு இடையே உள்ள நேர வித்தியாசத்தை கணக்கிட உதவுகிறது.

1. முதலில் எந்த தீர்க்க ரேகைகளில் இரண்டு இடங்கள் அமைந்துள்ளது என்பதை நாம் தெரிந்து கொள்ளவேண்டும்.

2. அடுத்ததாக, அந்த இரண்டு இடங்களின் தீர்க்கரேகையின் வித்தியாசத்தை (பாகையில்) கண்டுபிடிக்க வேண்டும். ஒருவேளை இரண்டு இடங்களும் முதன்மை தீர்க்கரேகையின் ஒரே பக்கத்தில் அமைந்து இருந்தால் அந்த இரு பாகைகளையும் கழித்து நேரவித்தியாசத்தை கணக்கிடலாம். இரு இடங்களும் முதன்மை தீர்க்க ரேகையின் வெவ்வேறு பக்கத்தில் அமைந்து இருந்தால் அவற்றின் பாகைகளைக் கூட்டி நேர வித்தியாசத்தைக் கணக்கிட முடியும்.

3. மூன்றாவதாக நாம் பாகை அளவையின் வித்தியாசத்தை 15 ஆல் வகுக்க வேண்டும். ஏனென்றால் ஒவ்வொரு மணிக்கும் 15 பாகைகள் உண்டு. இது இரண்டு இடங்களுக்கு இடையே உள்ள நேர வித்தியாசத்தைத் தருகிறது. எனவே ஒரு இடத்தின் நேரத்தையும், கணக்கிடவேண்டிய இடத்தின் தீர்க்கரேகையும் தெரிந்திருந்தால் நாம் எளிதாக இரண்டு இடங்களின் நேர வித்தியாசத்தைக் கணக்கிடலாம்.

இனி நாம் மற்றொரு வழியில் இரண்டு இடங்களுக்கும் இடையே உள்ள நேர வித்தியாசத்தை கணக்கிடலாம். அது சர்வதேச தேதி கோட்டை மையமாக வைத்து கணக்கிடுவதாகும். இந்தக் கோடானது பயன் படத்தக்க வகையில் பசிபிக் பெருங்கடலில் அமைக்கப்பட்டுள்ளது. எனவே, அருகிலிருக்கும் இரண்டு நகரங்களுக்கு ஒருநாள் வித்தியாசம் காணப்படுவதில்லை. இது சர்வதேச தேதிகோட்டில் அமைந்திருந்தாலும் அருகில் உள்ள இரண்டு இடங்களின் நேர வித்தியாசத்தை கணக்கிட முயற்சிக்கும் போது சற்று கடினமாக இருக்கலாம். இந்த கணக்கீடு முதன்மை தீர்க்க ரேகையை வைத்து கணக்கிட்டதைப் போலவே கணக்கிடப்படும். முதலில் இரண்டு பகுதிகளுக்கு இடையே உள்ள தீர்க்க ரேகையின் (°) பாகை (டிகிரி) வித்தியாசங்களை கண்டறிய வேண்டும். இதை நாம் இரு எண்களையும் கூட்டுவதன் மூலம் கணக்கிடலாம். பிறகு கூட்டப்பட்ட எண்ணை ஒவ்வொரு மணி நேரத்திற்கும் கிடைக்கும் 15° யால் வகுக்க வேண்டும். இது சர்வதேச தேதி கோட்டில் உள்ள இரு இடங்களுக்கும் இடையே உள்ள நேர வித்தியாசத்தைத் தருகிறது. மேலும் நமக்கு ஏற்கனவே தெரிந்த நேரத்தை கூட்டியோ கழித்தோ புதிய நேரமண்டலத்திலுள்ள புதிய நேரத்தை கணக்கிடலாம்.

நேர கணக்கீடுகளுக்கான எடுத்துக்காட்டுகள்:

இரண்டு தீர்க்க ரேகைகளுக்கு இடையில் உள்ள நேர வித்தியாசத்தை கண்டறிந்து 15 ஆல் வகுக்க வேண்டும் இது உங்களுக்கு இரண்டு இடங்களின் நேர வித்தியாசத்தைத் தரும். இரண்டாவதாக ஏற்கனவே தெரிந்த அந்த நாளின் மணி நேரத்தை கிழக்கு நோக்கிச் சென்றால் கூட்டவேண்டும், மேற்குநோக்கிச் சென்றால் கழிக்கவேண்டும். வேறுபட்ட நேர மண்டலத்தை எவ்வாறு கணக்கிட வேண்டும் என சில எடுத்துக்காட்டுகள் கீழே தரப்பட்டுள்ளன.

நீங்கள் இலண்டனில் இருப்பதாகக் கொள்வோம். அப்போது நேரம் பகல் 12:00 மணி என்றால் ஜப்பானில் என்ன நேரம் என்பதை அறிய வேண்டும். இதற்கு நீங்கள் இலண்டனில் இடஅமைப்பைத் தெரிந்து கொள்ள வேண்டும். இது சரியாக முதன்மை தீர்க்கரேகையில் அமைந்து இருப்பதால் 0° கிழக்காகவும் ஜப்பான் 135° கிழக்காகவும் அமைந்து உள்ளது. எனவே இரண்டு இடத்திற்கும் உள்ள வித்தியாசம் 135° எனக் கொள்ளலாம். இதை 15 ஆல் வகுத்தால் உங்களுக்கு 9 கிடைக்கும். எனவே இலண்டனுக்கும் ஜப்பானுக்கும் இடையில் 9 மணிநேரம் வித்தியாசம் காணப்படுகிறது என அறியலாம். ஜப்பான் இலண்டனிலிருந்து கிழக்கில் அமைந்துள்ளதால் நீங்கள் இந்த 9 மணி நேரத்தை 12 மணி நேரத்துடன் கூட்டவேண்டும். இப்பொழுது உங்களுக்கு 21 மணிநேரம் (இரவு 9 மணி) என விடைக் கிடைக்கும். அதாவது, லண்டனில் பகல் 12 மணி என்றால் ஜப்பானில் இரவு 9 ஆகும்.

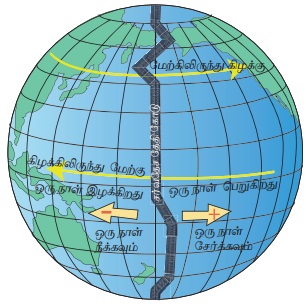
தற்போது நீங்கள் சர்வதேச தேதி கோட்டை கடந்து செல்வதாக கற்பனை செய்து கொள்ளுங்கள். நீங்கள் 135° கிழக்கில் உள்ள ஜப்பானில் இருப்பது போல நினைத்துக் கொள்ளுங்கள். நீங்கள் இப்பொழுது ஹவாயின் நேரத்தை அறிந்து கொள்ள விரும்புகிறீர்கள் என்றால் ஹவாய் 150° மேற்கில் உள்ளது. சர்வதேச தேதிக் கோட்டிற்கும் ஜப்பானின் அமைவிடத்திற்கும் உள்ள வித்தியாசம் 45° ஆகும். ஹவாயின் அமைவிடத்திற்கும் சர்வதேச தேதி கோட்டிற்கும் இடையே உள்ள வித்தியாசம் 30° ஆகும். எனவே இந்த இரண்டு வித்தியாசங்களையும் கூட்டி 15 ஆல் வகுத்தால் (45+30 /15 = 5) 5 மணி என வரும். இது ஒரு விசித்திரமான பகுதி ஆகும் ஏனென்றால் ஜப்பானும் ஹவாயும் வேறுவேறு நாட்களை கொண்டுள்ளது. சர்வதேசதேதி கோட்டிற்கு இடது பக்கம் வலது பக்கத்தை விட ஒருநாள் முன்னதாக இருக்கும். அதாவது, ஜப்பானில் வியாழன் மாலை 3 மணி என்றால் ஹவாயில் 5 மணி நேரத்தை கூட்டி இரவு 8 மணி எனக் கணக்கிட வேண்டும் ஆனால் சர்வதேச தேதி கோட்டைஹவாய் கிழக்காக கடந்து செல்வதால் நாம் ஒரு நாளை கழிக்கவேண்டும். அவ்வாறு கணக்கிடும் போது ஹவாயில் புதன் இரவு 8 மணி எனக் கணக்கிடுகிறோம்.

இப்பொழுது கவனியுங்கள் தீர்க்கரேகைகள் புவியைச் சுற்றி செல்லும் செங்குத்து கற்பனைக் கோடுகளாகும். 0° தீர்க்கரேகை என்பது முதன்மை தீர்க்கக்கோட்டை குறிக்கும். புவி தன் அச்சில் ஒருமுறை சுற்றிவர 24 மணி நேரத்தை எடுத்துக்கொள்கிறது. இந்த செயலின் போது புவியானது 360" முழுமையாக சுற்றுகிறது. எனவே, புவி ஒருமணி நேரத்தில் 360° / 24 = 15° ஐ கடக்கிறது. எனவே 1° தீர்க்கரேகை அதிகரிப்பது அல்லது குறைவது 4 நிமிடங்களைக் குறிக்கிறது.

360° = 24 மணிநேரம் = 1440 நிமிடங்கள் (24x60) 

15° தீர்க்க ரேகையின் வித்தியாசம் = ஒருமணிநேரம் 

1° தீர்க்க ரேகையின் வித்தியாசம் = 4 நிமிடங்கள்

தீர்க்க ரேகை கணக்கிடும் படிகள் :

1. முதலில் கணக்கிட வேண்டிய இரு இடங்களை குறிக்கவேண்டும் 

2. தீர்க்கரேகை வித்தியாசத்தை கண்டறியவும். 

3. தீர்க்கரேகையின் வித்தியாசத்தை நேரமாக மாற்றுதல்

4. புவி இயங்கும் திசைக்கு ஏற்ப நேரத்தை சரி செய்தல்

எடுத்துக்காட்டு 1

பொன்னி தன் பயணத்தை 0° இல் இருந்து பகல் 12 மணிக்கு ஆரம்பித்து கிழக்கு நோக்கி 10° தீர்க்கரேகைக்கு செல்கிறாள். பொன்னி தன்னுடைய இலக்கை எந்த நேரத்தில் அடைவாள் என்று கணக்கிடுக.

தீர்வு

ஆரம்பநேரம் = பகல் 12 மணி

செல்லவேண்டிய இடம் = 10° கிழக்கு தீர்க்க ரேகை நேரமாக மாற்றப்படுதல்

மணிநேரம் = 15°

4 நிமிடங்கள் = 1°

எனவே 10° = (4 X 10) நிமிடங்கள்

= 40 நிமிடங்கள்

அடைய வேண்டிய நேரம் = ஆரம்பநேரம் + கணக்கிடப்பட்ட நேரம்

= பகல் 12 + 40 நிமிடங்கள்

= 12: 40 நண்பகல்

எடுத்துக்காட்டு 2

A என்ற கிராமத்தின் நேரம் (தீர்க்கரேகை 75° மேற்கு) வெள்ளிக்கிழமை மாலை 5 மணி என்றால் தீர்க்கரேகையில் 120° கிழக்காக அமைந்துள்ள B கிராமத்தின் நேரத்தைக் கணக்கிடவும்.

தீர்வு

360° = 24 மணிநேரம்

15° = 1 மணி 

1° = 4 நிமிடங்கள்

கிராமம் A = 75° மேற்கு

கிராமம் B = 120° கிழக்கு 

கூட்டவும் (மேற்கு மற்றும் கிழக்கு) 

(75 + 120)o = 195° 

195° ஐ 15 ஆல் வகுக்கவும் = 13 மணி

சென்றடைய வேண்டிய நேரம் = ஆரம்பநேரம் + கணக்கிடப்பட்ட நேரம்

= 5 + 13 மணிநேரம் = 18 மணி 

18 மணி நேரம் என்பது மாலை 6.00 மணி ஆகும். 

விடை = சனிக்கிழமை மாலை 6.00

எடுத்துக்காட்டு 3

தற்பொழுது 15° கிழக்கில் உள்ள நைஜிரியாவில் காலை 10 மணி என்றால் அதே நேரத்தில் 75° மேற்கு தீர்க்கரேகையில் அமைந்துள்ள நியூயார்க் நகரத்தின் உள்நாட்டு நேரத்தை கணக்கிடுக.

தீர்வு 

ஆரம்ப நேரம் = காலை 10.00 மணி 

நியூயார்க் = 75° மேற்கு 

நைஜிரியா = 15° கிழக்கு 

இரண்டையும் கூட்டவும் = (மேற்கு + கிழக்கு) 

(75°+15°) = 90°

90° / 15° =  6 மணிநேரம்

அடைய வேண்டிய நேரம் = ஆரம்ப நேரம் + கணக்கிடப்பட்ட நேரம்

= காலை 10 + 6 மணிநேரம்

= 16 மணிநேரம் என்பது மாலை 4 மணி ஆகும்.

விடை : மாலை 4 மணி