வகை நுண்கணிதம்

அத்தியாயம் – 9

வகை நுண்கணிதம் எல்லைகள் மற்றும் தொடர்ச்சித் தன்மை 

DIFFERENTIAL CALCULUS LIMITS AND CONTINUITY

“மனிதர்கள் மறையலாம், அவர்களின் செயல்கள் மறைவதில்லை” − அகஸ்டின் − லூயிஸ் கோசி

அறிமுகம் (Introduction)

நுண்கணிதம் என்பது மாற்றத்தின் வீதங்கள் தொடர்பானது. அறிவியலின் அனைத்துப் பிரிவுகளிலும் மாறுதலின் வீதங்கள் உள்ளன. கணிதவியலில் அறிஞர்கள் ஒரு வளைவரையின் மீது அமையும் நேர்க்கோட்டில் ஏற்படும் மாறுவீதத்தைக் கணக்கிடுவதில் ஆர்வமாக இருக்கின்றனர். அதே சமயம் இயற்பியல் அறிஞர்கள் ஒரு நகரும் பொருளின் இடப்பெயர்ச்சியின் மாறுவீதம், மற்றும் அதன் திசைவேகம் ஆகியவற்றைக் கணக்கிடுவதில் ஆர்வம் காட்டுகின்றனர். வேதியியலாளர்கள் ஒன்று அல்லது அதற்கு மேற்பட்ட மூலகங்கள் சேர்ந்து ஒன்று அல்லது அதற்கு மேற்பட்ட பொருட்களைக் கொடுக்கும் வேதி வினையின் வீதத்தைக் கணக்கிட விரும்புகின்றனர்.

ஓர் உயிரியலாளர், விலங்குகள் அல்லது தாவரங்களின் மொத்த எண்ணிக்கையில் குறிப்பிட்ட சில விலங்குகள் அல்லது தாவரங்களில் ஏற்படும் மாற்றங்களை ஆய்வு செய்ய விரும்புகின்றார். மேலும் இரத்த நாளங்கள் அல்லது தமனிகளில் உள்ள இரத்த ஓட்டத்தின் வீதத்தைக் கணக்கிடவும், இரத்த ஓட்டம் எந்த இரத்த நாளங்கள்/தமனிகளில் குறைவாக/அதிகமாக உள்ளது என்பதைக் காணவும் விழைகின்றார்.

பொருளியலாளர்கள், இறுதிநிலைத் தேவை, இறுதிநிலை வருவாய் மற்றும் இறுதிநிலை இலாபம் ஆகியவற்றை, தேவை, வருவாய் இலாபச் சார்புகளின் மாறுவீதம் மூலம் காண்கின்றனர்.

புவியியலாளர்கள், உருகிய பாறைக் குழம்புகள் சுற்றியுள்ள பாறைகளுடன் வெப்பத்தைக் கடத்தி குளிர்வதற்கான வீதத்தைக் கணக்கிடுவதில் ஆர்வம் காட்டுகின்றனர். ஒரு பொறியாளர், மேல்நிலைத் தொட்டிக்குத் தண்ணீர் ஏற்றும் வீதம் மற்றும் தொட்டியிலிருந்து தண்ணீர் வெளியேறும் வீதத்தைக் கணக்கிட விரும்புகின்றார். நகர்ப்புறப் புவியியலாளர், ஒரு நகரம் விரிவுபடுத்தப்படும்போது ஏற்படும் மக்கள்தொகை அடர்த்தி வீதத்தினைக் கணக்கிட விரும்புகின்றார்.

வானிலையாளர்கள் உயரத்திற்குத் தகுந்தாற்போல் வளிமண்டல அழுத்தத்தில் ஏற்படும் மாறுதலின் மாறுவீதத்தைக் கணக்கிடுவதில் ஆர்வம் காட்டுகின்றனர்.

உளவியலில் கற்றல் கோட்பாட்டில் ஆர்வமுள்ளவர்கள், கற்றல் வளைவரையைப் பற்றிப் படிக்கின்றனர். இது ஒருவரின் பயிற்சிக் காலத்தைப் பொறுத்த கற்றல் திறன் செயல்பாட்டின் வளைவரையாகும். காலத்தைப் பொறுத்துத் திறன் மேம்பாட்டின் வீதத்தின் அடிப்படையில் ஆர்வத்தைக் காணலாம்.

நாம் ஓர் இருட்டு அறையில் நுழையும்போது சுற்றியுள்ள பொருட்களைக் காண அதிக ஒளி உள் செல்ல ஏதுவாக நமது கண்பாவை விரிவடைந்து பொருட்களைத் தெளிவாகக் காண உதவுகிறது. அதற்கு நேர்மாறாக நாம் அதிக வெளிச்சமுள்ள ஓர் அறையில் நுழையும்போது அதிக வெளிச்சத்தினால் (ஒளியினால்) நமது பார்வைத் திறன் பாதிக்காத வகையில் நமது கண்பாவை சுருங்கி உள்ளே செல்லும் ஒளியின் அளவைக் குறைக்கின்றது. ஆராய்ச்சியாளர்கள், இது போன்ற செயல்பாடுகளின் வழிமுறையைக் கணித எல்லைகள் மூலம் காண்கின்றனர்.

இயற்பியலில் திசைவேகம், அடர்த்தி, மின்னோட்டம், மின்னாற்றல் மற்றும் வெப்பநிலையின் மாறுநிலை; வேதியியலில் எதிர்வினையின் வீதம் மற்றும் ஒருங்குத் தன்மை; உயிரியியலில் வளர்ச்சி வீதம் மற்றும் இரத்த ஓட்டத்தின் வேகம்; பொருளியியலில் இறுதிநிலைச் செலவு மற்றும் இறுதிநிலை இலாபம்; புவியியலில் வெப்ப ஓட்டத்தின் வீதம்; உளவியலில் செயல்திறன் ஆகியவை வகைக்கெழு என்ற ஒரே ஒரு கணிதக் (கோட்பாட்டின்) கருத்தாக்கத்தின் அடிப்படையில் அமைகிறது.

மேற்கூறியவை கணிதத்தின் திறன் அதன் உள்நுட்பமான தன்மையின் அடிப்படையில் உள்ளதற்கான எடுத்துக்காட்டுகளாகும். ஒரே ஒரு நுட்பமானக் கணிதக் கருத்தாக்கம் (வகைக்கெழு) அறிவியலின் பல்வேறு பிரிவுகளில் பலவிதமான விளக்கங்களைத் தருகின்றது. நாம் கணிதக் கருத்துருக்களை உருவாக்கும்போது அவற்றின் முடிவுகள் அறிவியலின் பல்வேறு பிரிவுகளில் பயன்படுத்தப்படுகின்றன. அறிவியலின் ஒவ்வொரு பிரிவிலும் உருவாகும் தனிப்பட்ட கருத்துருக்களைக் காட்டிலும் இது ஆற்றலுடையது.

பழங்காலத்தின் மிகச் சிறந்த படைப்புகளில் ஒன்று யூக்ளிடின் வடிவியல் ஆகும். இந்த முக்கியமான படைப்புக்கு இணையாக எந்தக் கண்டுபிடிப்பும் இரண்டாயிரம் ஆண்டுகளாக நுண்கணிதம் கண்டுபிடிக்கும்வரை நிகழவில்லை.

நுண்கணிதமானது இங்கிலாந்தில் சர் ஐசக் நியூட்டன் (1642−1727) மற்றும் ஜெர்மனியில் காட்ஃபிரைட் வில்ஹெல்ம் லிபினிட்ஸ் (1646 -1716) என்பவர்களால் 17-ஆம் நூற்றாண்டின் இறுதியில் உருவாக்கப்பட்டது.

நியூட்டனின் கணித ஆர்வத்திற்குக் காரணம், அவருடைய காலத்தில் அவருக்குக் கிடைத்த மிகச் சிறந்த Euclid’s Elements மற்றும் Descartio La Geometric ஆகிய இரு புத்தகங்களாகும். அவர்,  அவருக்கு முன்னர் வாழ்ந்த கலிலியோ மற்றும் பெர்மாட் போன்ற ஆராய்ச்சியாளர்கள் பற்றியும் அவர்களின் கண்டுபிடிப்புகள் பற்றியும் அறிந்திருந்தார்.

1664−ன் முடிவில் நியூட்டன் அவருடைய காலத்தில் கணித அறிவை முழுமையாகப் பெற்று அதன்பின் மேலும் வளர்த்துக் கொண்டார். 1665−ல் தொடர்ந்து மாறக்கூடிய தூரங்கள், வெப்பநிலைகள் போன்றவற்றின் மாறுகின்ற வீதம் பற்றி அவருடைய ஆராய்ச்சியை ஆரம்பித்தார். இந்த ஆராய்ச்சியின் விளைவுதான் இன்று நாம் காணும் வகைநுண்கணிதம் ஆகும். இன்று கணிதவியல் படிப்பவர்கள் அனைவரும் ஐசக் நியூட்டனின் கண்டுபிடிப்புகளில் பயணிக்கின்றனர்.

லிபினிட்ஸின் கணித ஆராய்ச்சிக் கட்டுரைகள் அவர் 1682-ல் ஆரம்பித்த ‘Acta Eruditorum’ என்ற சஞ்சிகையில் பிரசுரமானது. இந்த சஞ்சிகையில் அவருடைய நுண்கணிதம் பற்றிய கட்டுரைகள் இடம்பெற்றன. இதுவே யார் முதலில் நுண்கணிதம் கண்டுபிடித்தது என நியூட்டனுடன் ஏற்பட்ட முரண்பாட்டிற்குக் காரணமாக இருந்தது. நுண்கணிதத்தின் முக்கிய முடிவுகளையும், தற்போது பயன்படுத்தும் வகைக்கெழு குறியீட்டையும் முதன்முதலாகப் பயன்படுத்தியவர் லிபினிட்ஸ் ஆவார்.

பாரிசில் 1789-ம் ஆண்டு பிறந்து 19-ஆம் நூற்றாண்டின் முதல் அரைப்பகுதியின் முதன்மையான கணிதமேதையாக அறியப்பட்டவர் அகஸ்டின்–லூயிஸ்கோஷி (1789-1857) ஆவார். கோஷி நுண்கணிதத்திற்குப் பல பங்களிப்புகள் செய்திருக்கின்றார். 1829இல் இவருடைய ‘Lecons Le calcul differential’ என்ற புத்தகத்தில் முதன்முதலாக எல்லைகள் பற்றிய தெளிவான வரையறையைத் தந்துள்ளார். மேலும் வகைக்கெழுவை வித்தியாசங்களின் விகிதத்தின் எல்லையாக, அதாவது,

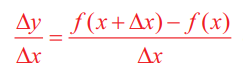
Δy/Δx = [f ( x + Δx) − f(x)] /Δx −ன் எல்லை எனத் தந்துள்ளார்.

எல்லைகளின் துல்லியமான (∈ − δ) வரையறை, தொடர்ச்சி மற்றும் வகைக்கெழு பற்றிய துல்லியமான கருத்துருக்களைக் கார்ல் வொயர்ஸ்ட்ராஸ் (1815−1897) என்ற ஜெர்மன் கணிதமேதை தந்துள்ளார்.

நுண்கணிதம் என்றால் என்ன?

அளவுகளின் அல்லது கணியங்களின் மாறுவீத கணிதம் நுண்கணிதம் ஆகும். மேலும் அன்றாட வாழ்வில் ஆராய்ச்சியாளர்கள், பொறியாளர்கள், பொருளியல் வல்லுனர்கள் பயன்படுத்தும் தொடுகோடுகள், சாய்வுகள், பரப்பு, கன அளவு, வில்லின் நீளம், நடுக்கோட்டுச் சந்தி, விளைவுத் தன்மை போன்ற கருத்துகளின் கணிதமாகவும் நுண்கணிதம் உள்ளது.

நுண்கணிதத்திற்கு முந்தைய புகுமுக நுண்கணிதத்தில், திசைவேகம் முடுக்கம், தொடுகோடுகள், சாய்வுகள் போன்றவைகள் வரையறுக்கப்பட்டிருப்பினும் நுண்கணிதத்திற்கும் புகுமுக நுண்கணிதத்திற்கும் அடிப்படையில் சில வேறுபாடுகள் உள்ளன. நுண்கணிதத்திற்கு முந்தைய புகுமுக நுண்கணிதம் நகராத தன்மையை உரைப்பதாகவும் நுண்கணிதம் நகரும் தன்மையை உரைப்பதாகவும் உள்ளன என்பதனைக் கவனத்தில் கொள்ள வேண்டும்.

• மாறாத திசைவேகத்தில் பயணிக்கும் ஒரு பொருளினைப் பகுப்பாய்வு செய்ய புகுமுக நுண்கணிதம் போதுமானது. ஆனால் முடுக்கிவிடப்பட்ட ஒரு பொருளின் திசைவேகத்தைப் பகுப்பாய்வு செய்ய நுண்கணிதம் தேவைப்படுகின்றது.

• ஒரு நேர்க்கோட்டின் சாய்வைப் பகுப்பாய்வு செய்ய புகுமுக நுண்கணிதம் போதுமானது. ஆனால் ஒரு வளைவரையின் சாய்வினைப் பகுப்பாய்வு செய்ய நுண்கணிதம் தேவைப்படுகின்றது. 

• ஒரு வட்டத்தின் தொடுகோட்டைப் பகுப்பாய்வு செய்யப் புகுமுக நுண்கணிதம் போதுமானது. ஆனால் ஏதேனுமொரு வளைவரையின் தொடுகோட்டைப் பகுப்பாய்வு செய்ய நுண்கணிதம் தேவைப்படுகின்றது.

• ஒரு செவ்வகத்தின் பரப்பைப் பகுப்பாய்வு செய்யப் புகுமுக நுண்கணிதம் போதுமானது. ஒரு வளைவரை ஏற்படுத்தும் பரப்பைக் காண நுண்கணிதம் தேவைப்படுகின்றது.

மேற்கண்ட ஒவ்வொரு சூழலிலும் உள்ள பொதுவான உத்தி எல்லைச் செயல்முறை மூலம் புகுமுக நுண்கணிதத்தினை நுண்கணிதமாக மறுசீரமைக்கும் செயலாகும். நுண்கணிதம் என்றால் என்ன? என்ற கேள்விக்கு விடையளிக்கும் விதமாக நுண்கணிதத்தை மூன்று நிலைகள் உடைய "எல்லை இயந்திரம்" எனலாம். இதில் முதல் நிலையானது நேர்க்கோட்டின் சாய்வு, செவ்வகத்தின் பரப்பு காணுதல் போன்ற புகுமுக நுண்கணிதம் ஆகும். இரண்டாம் நிலை எல்லைச் செயல்பாடு ஆகும். மூன்றாம் நிலை புதிய பரிமாணமான வகையிடுதல் மற்றும் தொகையிடுதல் ஆகும்.

நுண்கணிதத்தை ஒரு செயல்முறையாக அல்லாமல் புதிய சூத்திரங்களின் தொகுப்பாக படிக்க முயற்சிப்பவர்கள், புரிதல், தன்னம்பிக்கை மற்றும் திருப்தியை இழப்பார்கள் என எச்சரிக்கப்படுகின்றனர்.

கற்றலின் நோக்கங்கள்

இப்பாடப்பகுதி நிறைவுறும்போது மாணவர்கள் அறிந்திருக்க வேண்டியவைகளாக 

• வடிவியல் செயல்முறையாக எல்லை/தொடர்ச்சிக் கருத்துருக்களைக் காணல் 

• எல்லை/தொடர்ச்சிக் கருத்துருகளை அன்றாட வாழ்க்கை செயல்களோடு தொடர்புபடுத்துதல் 

• எல்லை/தொடர்ச்சியை நுண்கணிதத்தின் இதயம் மற்றும் உயிர்த் துடிப்பாக உணர்வது 

• விஞ்ஞான உலகத்தில் நடைபெறும் ஒவ்வொரு மாற்றத்தினை அளவிடுதலுக்கும் மற்றும் கணிதமயமாக்கலுக்கும் எல்லை/தொடர்ச்சியினை ஒரு கருவியாகப் பயன்படுத்துதல் 

• எல்லை/தொடர்ச்சிக் கருத்துருவை வாழ்க்கைச் சூழல் மூலம் திடப்படுத்துதல் ஆகியவை எதிர்பார்க்கப்படுகின்றன.