ஒரு புள்ளியில் தொடர்ச்சியான சார்புகளின் எடுத்துக்காட்டுகள் (Examples of functions continuous at a point)

ஒரு புள்ளியில் தொடர்ச்சியான சார்புகளின் எடுத்துக்காட்டுகள் (Examples of functions continuous at a point)

(1) மாறிலிச் சார்பு ℝ −ன் எல்லா புள்ளியிலும் தொடர்ச்சியானது .

f(x) = k,k ∈ ℝ என்பது ஒரு மாறிலி. x0, ∈ ℝ, எனில் f(x0) = k. மேலும்

(2) மிகை முழு எண் அடுக்கு உடைய அடுக்குச் சார்புகள் ℝ −ன் எல்லா புள்ளிகளிலும் தொடர்ச்சியானவை. f(x) = xn எனில், f −ன் சார்பகம் ℝ (− ∞, ∞) மற்றும் எல்லைத் தேற்றத்தின்படி

(3) p(x) = a0xn + a1xn−1 + ... + a n−1x + an , a0 ≠ 0 என்ற பல்லுறுப்புக் கோவைகள் ℝ −ன் எல்லா புள்ளிகளிலும் தொடர்ச்சியானது. எல்லைத் தேற்றப்படி

 (4) பல்லுறுப்புக் கோவைகளின் பின்னம் அதாவது   என்ற விகிதமுறு சார்புகள் எல்லாப் புள்ளிகளிலும் தொடர்ச்சியானவை.

(5) வட்டச் சார்புகளான sin x மற்றும் cos x என்பவை அவற்றின் சார்பகம் ℝ = (− ∞, ∞) −ல் உள்ள எல்லாப் புள்ளிகளிலும் தொடர்ச்சியானவை.

இதன் விளைவாக, எல்லைகளின் தலைகீழி மற்றும் வகுத்தல் விதிகிளின்படி, tan x, cot x, cosec x, sec x போன்ற சார்புகள் அவற்றிற்கு பொருத்தமான சார்பகங்களில் தொடர்ச்சியானவை.

(6) f(x ) = x1/n போன்ற n−ஆம் படி மூல சார்புகள் அவற்றிற்கு பொருத்தமான சார்பகங்களில் தொடர்ச்சியானவை. காரணம்

(7) தலைகீழிச் சார்பு f (x) = 1/x  ,  x = 0 −ல் அது தொடர்ச்சியற்றது. ஆனால் ℝ −{0} −ல் எல்லா புள்ளிகளுக்கும் f தொடர்ச்சியானது.

(8)

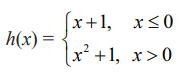
h−ன் சார்பகம் எல்லா மெய்யெண்கள் ஆகும். மேலும்

எனவே x = 0−ல் h ஒரு தொடர்ச்சியான சார்பாகும். மேலும் (− ∞, 0) மற்றும் (0, ∞)−ல் h ஒரு தொடர்ச்சியான சார்பு. எனவே, (– ∞, ∞)−ல் h(x) ஒரு தொடர்ச்சியானது.

(11) படிக்குறிச் சார்பு f(x) = ex, ℝ −ன் எல்லா புள்ளிகளுக்கும் தொடர்ச்சியானது.

(12) மடக்கைச் சார்பு f(x) = log x (x > 0), (0, ∞)−ல் தொடர்ச்சியானது.