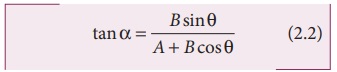தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் - வெக்டர்களின் கூடுதல் (வெக்டர்களின் முக்கோணவிதி) | 11th Physics : UNIT 2 : Kinematics
11வது இயற்பியல் : அலகு 2 : இயக்கவியல்
வெக்டர்களின் கூடுதல் (வெக்டர்களின் முக்கோணவிதி)
வெக்டர்களின் கூடுதல்
வெக்டர்கள், எண்மதிப்பு மற்றும் திசை இவ்விரண்டையும் பெற்றுள்ளதால், சாதாரண இயற்கணித முறையில் அவற்றின் கூடுதலைக் காண இயலாது. எனவே, வெக்டர்களை வடிவியல் முறையிலோ அல்லது பகுப்பு முறையிலோ சில விதிகளைப்பயன்படுத்தி அவற்றின் கூடுதலைக் காண வேண்டும். இம்முறைக்கு வெக்டர் இயற்கணிதம் என்று பெயர். ஒன்றுக்கொன்று சாய்ந்த நிலையில் உள்ள இரண்டு வெக்டர்களின் கூடுதலை (தொகுபயன்) (i) வெக்டர்களின் முக்கோணக் கூட்டல் விதி (ii) வெக்டர்களின் இணைகரவிதி ஆகிய இரண்டு விதிகளைப் பயன்படுத்திக் காணலாம்.
வெக்டர்களின் முக்கோண விதி:
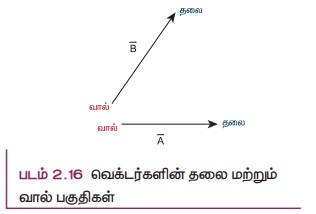
படம் 2.16 யில் காட்டப்பட்டுள்ள ![]() மற்றும்
மற்றும் ![]() என்ற இரண்டு வெக்டர்களின் தொகுபயனை வெக்டர்களின் முக்கோணக் கூட்டல் விதியைப் பயன்படுத்தி காணலாம்.
என்ற இரண்டு வெக்டர்களின் தொகுபயனை வெக்டர்களின் முக்கோணக் கூட்டல் விதியைப் பயன்படுத்தி காணலாம்.
இரண்டு வெக்டர்களின் தொகுபயனை, வெக்டர்களின் முக்கோணவிதியினை பயன்படுத்தி கீழ்க்கண்டவாறு காணலாம். ![]() மற்றும்
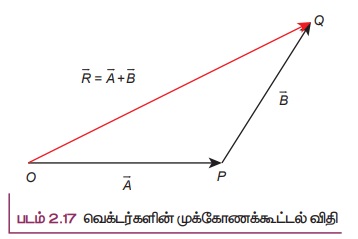
மற்றும் ![]() என்ற இரண்டு சுழியற்ற வெக்டர்கள் வரிசைப்படி ஒரு முக்கோணத்தின் அடுத்தடுத்த பக்கங்களாகக் கருதப்பட்டால், அவற்றின் தொகுபயன், எதிர்வரிசையில் எடுக்கப்பட்ட அம்முக்கோணத்தின் மூன்றாவது பக்கத்தினால் குறிப்பிடப்படும். இது படம் 2.17 யில் காட்டப்பட்டுள்ளது. இது பின்வருமாறு விளக்கப்பட்டுள்ளது.
என்ற இரண்டு சுழியற்ற வெக்டர்கள் வரிசைப்படி ஒரு முக்கோணத்தின் அடுத்தடுத்த பக்கங்களாகக் கருதப்பட்டால், அவற்றின் தொகுபயன், எதிர்வரிசையில் எடுக்கப்பட்ட அம்முக்கோணத்தின் மூன்றாவது பக்கத்தினால் குறிப்பிடப்படும். இது படம் 2.17 யில் காட்டப்பட்டுள்ளது. இது பின்வருமாறு விளக்கப்பட்டுள்ளது.
![]() வெக்டரின் தலைப்பகுதி
வெக்டரின் தலைப்பகுதி ![]() வெக்டரின் வால்பகுதியோடு இணைக்கப்பட்டுள்ளது.
வெக்டரின் வால்பகுதியோடு இணைக்கப்பட்டுள்ளது. ![]() வெக்டர் மற்றும்
வெக்டர் மற்றும் ![]() வெக்டர்களுக்கு இடையே உள்ள கோணம் θ என்க.
வெக்டர்களுக்கு இடையே உள்ள கோணம் θ என்க. ![]() வெக்டரின் வால்பகுதியையும்,
வெக்டரின் வால்பகுதியையும், ![]() இன் தலைப்பகுதியையும் இணைத்தால் தொகுபயன் வெக்டர்
இன் தலைப்பகுதியையும் இணைத்தால் தொகுபயன் வெக்டர் ![]() கிடைக்கும். வடிவியல் முறையில் தொகுபயன் வெக்டர்
கிடைக்கும். வடிவியல் முறையில் தொகுபயன் வெக்டர் ![]() இன் எண்மதிப்பு அதன் நீளம் OQ க்குச் சமம். மேலும் தொகுபயன் வெக்டர்
இன் எண்மதிப்பு அதன் நீளம் OQ க்குச் சமம். மேலும் தொகுபயன் வெக்டர் ![]() மற்றும்
மற்றும் ![]() வெக்டருக்கு இடையே உள்ள கோணம், தொகுபயன் வெக்டரின் திசையைக் கொடுக்கும். எனவே
வெக்டருக்கு இடையே உள்ள கோணம், தொகுபயன் வெக்டரின் திசையைக் கொடுக்கும். எனவே 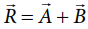 என எழுதலாம். ஏனெனில்
என எழுதலாம். ஏனெனில்
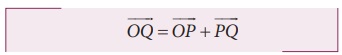
(1) தொகுபயன் வெக்டரின் எண்மதிப்பு:
தொகுபயன் வெக்டரின் எண்மதிப்பு மற்றும் திசை கீழ்க்கண்டவாறு கணக்கிடப்படுகிறது.
படம் 2.18 இல் ABN என்ற செங்கோண முக்கோணத்தைக் கருதுக. படத்தில் OA என்ற பக்கத்தை ON வரை நீட்டுவதன் மூலம் ABN என்ற செங்கோண முக்கோணம் கிடைக்கிறது.
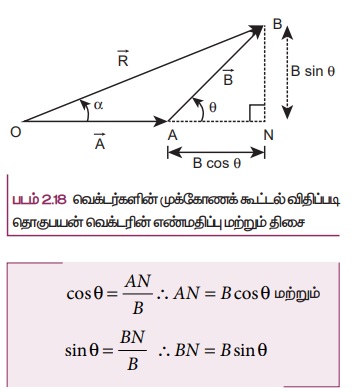
∆OBN ல் OB2 = ON 2 + BN 2
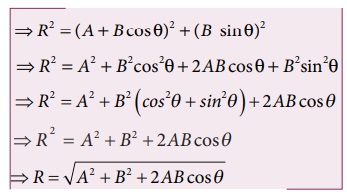
இச்சமன்பாடு ![]() மற்றும்
மற்றும் ![]() வெக்டர்களின் தொகுபயன் வெக்டரின் எண்மதிப்பைத் தருகிறது.
வெக்டர்களின் தொகுபயன் வெக்டரின் எண்மதிப்பைத் தருகிறது.
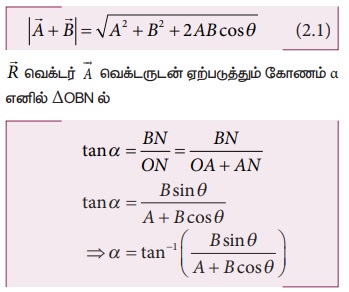
(2) தொகுபயன் வெக்டரின் திசை:
![]() மற்றும்
மற்றும் ![]() வெக்டர் இடையே உள்ள கோணம் θ எனில்
வெக்டர் இடையே உள்ள கோணம் θ எனில்
வெக்டர்களின் கூடுதல் தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள்
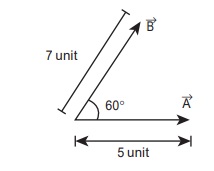
எடுத்துக்காட்டு 2.1
![]() மற்றும்
மற்றும் ![]() என்ற இரண்டு வெக்டர்கள் ஒன்றுக்கொன்று 60° கோணத்தில் சாய்ந்த நிலையில் உள்ளன. அவற்றின் எண்மதிப்புகள் முறையே 5 அலகுகள் மற்றும் 7 அலகுகள் ஆகும். தொகுபயன் வெக்டரின் எண்மதிப்பு மற்றும்
என்ற இரண்டு வெக்டர்கள் ஒன்றுக்கொன்று 60° கோணத்தில் சாய்ந்த நிலையில் உள்ளன. அவற்றின் எண்மதிப்புகள் முறையே 5 அலகுகள் மற்றும் 7 அலகுகள் ஆகும். தொகுபயன் வெக்டரின் எண்மதிப்பு மற்றும் ![]() p யைப் பொருத்து தொகுபயன் வெக்டரின் திசை ஆகியவற்றைக் காண்க.
p யைப் பொருத்து தொகுபயன் வெக்டரின் திசை ஆகியவற்றைக் காண்க.
தீர்வு
வெக்டர்களின் முக்கோணவிதிப்படி
கீழ்க்கண்ட படம் வெக்டர்களின் கூடுதலை எவ்வாறு முக்கோணவிதியின் அடிப்படையில் காணலாம் என்பதை விளக்குகிறது.
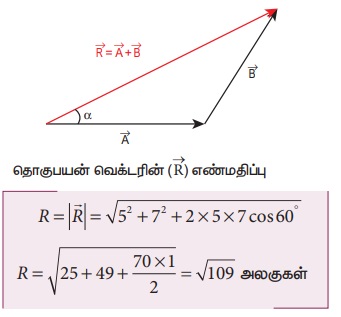
![]() மற்றும்
மற்றும் ![]() க்கு இடையே உள்ள கோணம் α (தொகுபயன் வெக்டரின் திசை) கீழ்க்கண்டவாறு கணக்கிடப்படுகிறது.
க்கு இடையே உள்ள கோணம் α (தொகுபயன் வெக்டரின் திசை) கீழ்க்கண்டவாறு கணக்கிடப்படுகிறது.