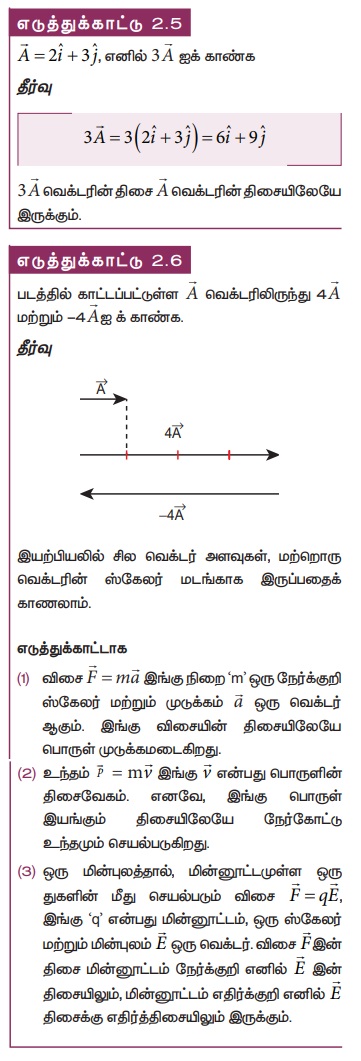
ஒரு ஸ்கேலரால் வெக்டரைப் பெருக்குதல்

ஒரு ஸ்கேலரால் வெக்டரைப் பெருக்குதல்

ஒரு ஸ்கேலரால் வெக்டரைப் பெருக்கும் போது, மற்றொரு வெக்டர் கிடைக்கும். λ என்ற ஒரு நேர்க்குறி எண்ணை வெக்டருடன் பெருக்கும் போது கிடைக்கும் வெக்டர் λ ஆகும். இதன் திசை இன் திசையிலேயே இருக்கும். ஆனால் λ ஒரு எதிர்க்குறி எண் எனில் λ இன் திசை வெக்டரின் திசைக்கு எதிர்த்திசையில் இருக்கும்.

இரண்டு வெக்டர்களின் ஸ்கேலர் பெருக்கல் (புள்ளிப் பெருக்கல்)

வரையறை

இரண்டு வெக்டர்களின் ஸ்கேலர் பெருக்கல் (புள்ளிப் பெருக்கல்) என்பது, அவ்விரண்டு வெக்டர்களின் எண்மதிப்புகள் மற்றும் அவ்விரண்டு வெக்டர்களுக்கு இடைப்பட்ட கோணத்தின் கொசைன் மதிப்பு ஆகியவற்றின் பெருக்கல் பலனுக்குச் சமமாகும். 

மற்றும் என்ற இரண்டு வெக்டர்களுக்கு இடைப்பட்ட கோணம் θ எனில் அவற்றின் ஸ்கேலர் பெருக்கல் கீழ்க்காணுமாறு வரையறை செய்யப்படுகிறது.

 ⋅  = AB cos θ. இங்கு A மற்றும் B ஆகியவை மற்றும் வெக்டர்களின் எண்மதிப்புகள் ஆகும்.

பண்புகள் 

(i) ஸ்கேலர் பெருக்கலின் தொகுபயன் மதிப்பு எப்போதும் ஒரு ஸ்கேலர் ஆகும். இரண்டு வெக்டர்களுக்கு இடையே உள்ள கோணம் குறுங்கோணம் எனில் (θ < 90°) ஸ்கேலர் பெருக்கலின் எண்மதிப்பு நேர்குறியுடனும், விரிகோணம் எனில் (90° < θ < 180°) எதிர்குறியுடனும் இருக்கும். 

(ii) ஸ்கேலர் பெருக்கல் பரிமாற்று விதிக்கு உட்பட்டது. அதாவது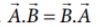  

(iii) ஸ்கேலர் பெருக்கல் பங்கீட்டு விதிக்கு உட்பட்டது அதாவது

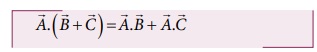
(iv) ஸ்கேலர் பெருக்கலின் படி இரண்டு வெக்டர்களுக்கு இடைப்பட்ட கோணம்

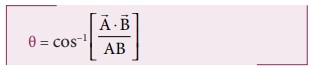
(v) இரண்டு வெக்டர்கள் இணையாக உள்ளபோது அதாவது θ = 0°, எனில் அவற்றின் ஸ்கேலர் பெருக்கல் பெருமம் ஆகும். ஏனெனில் Cos 0° = 1

(vi) இரண்டு வெக்டர்கள் ஒன்றுக்கொன்று எதிராக உள்ள போது அதாவது θ = 180° எனில், அவற்றின் ஸ்கேலர் பெருக்கல் சிறுமம் ஆகும். ஏனெனில் COS 180° = -1

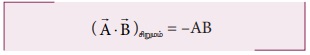
(vii) இரண்டு வெக்டர்கள் ஒன்றுக்கொன்று செங்குத்தாக உள்ள போது, அதாவது θ = 90° எனில் அவற்றின் ஸ்கேலர் பெருக்கல் சுழியாகும். ஏனெனில் COS 90° = 0 எனவே அந்த வெக்டர்களை, செங்குத்து வெக்டர்கள் (orthogonal vectors) என அழைக்கலாம் 

(vii) ஒரு வெக்டர், அதே வெக்டருடன் ஸ்கேலர் பெருக்கல் செய்யப்பட்டால், அதற்கு தற்சார்பு ஸ்கேலர் பெருக்கல் என்று பெயர். 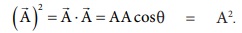இங்கு கோணம் θ = 0°

A -இன் எண்மதிப்பு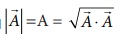  

(ix) ஓரலகு வெக்டர் ஐக் கருதும்போது

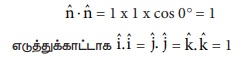
(x) செங்குத்து ஓரலகு வெக்டர்களைக் கருதும் போது

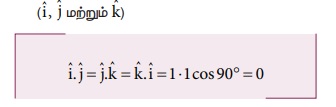
(xi) வெக்டர் கூறுகளின் அடிப்படையில் மற்றும் வெக்டர்களின் ஸ்கேலர் பெருக்கலைக் கீழ்க்கண்டவாறு எழுதலாம்.

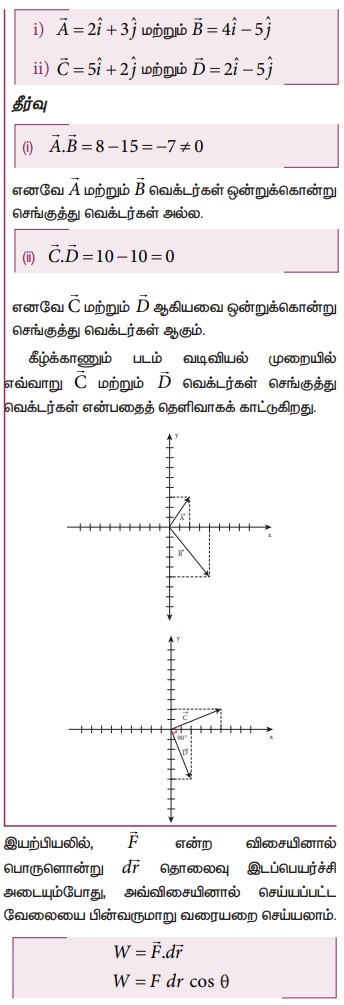
எடுத்துக்காட்டு 2.8

கொடுக்கப்பட்ட வெக்டர்கள் ஒன்றுக்கொன்று செங்குத்து வெக்டர்களா என ஆராய்க.

விசையினால் செய்யப்பட்ட வேலை என்பது, விசை வெக்டருக்கும், இடப்பெயர்ச்சி வெக்டருக்கும் இடையேயான ஸ்கேலர் பெருக்கல் ஆகும். வேலையைப் போலவே, மேலும் பல்வேறு இயற்பியல் அளவுகளும் ஸ்கேலர் பெருக்கலினால் வரையறை செய்யப்பட்டுள்ளன என்பதை நினைவில் கொள்ளவும்.

சீரான வட்ட இயக்கத்தில் மையநோக்கு விசை, பொருளின் இடப்பெயர்ச்சிக்குச் செங்குத்தாக செயல்படுவதால், மையநோக்கு விசையினால் பொருளின் மீது செய்யப்பட்ட வேலை சுழியாகும்.

இரண்டு வெக்டர்களின் வெக்டர் பெருக்கல்

வரையறை 

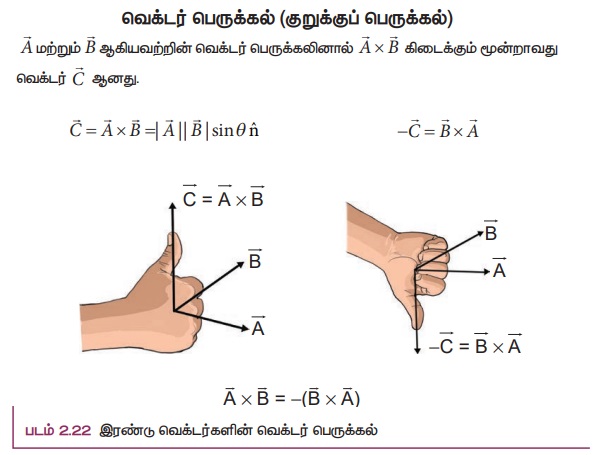
இரண்டு வெக்டர்களின், வெக்டர் பெருக்கல் அல்லது குறுக்கு பெருக்கல் செய்யும் போது கிடைக்கும் தொகுபயன் வெக்டரின் எண்மதிப்பானது, அவ்விரு வெக்டர்களின் எண்மதிப்புகளின் பெருக்கல் பலன் மற்றும் அவ்வெக்டர்களுக்கு இடைப்பட்ட கோணத்தின் சைன்மதிப்பு ஆகியவற்றின் பெருக்கல் பலனுக்குச் சமமாகும். மேலும் வலதுகை திருகுவிதி அல்லது வலதுகை பெருவிரல் விதியின் அடிப்படையில், தொகுபயன் வெக்டரின் திசையானது, இரண்டு வெக்டர்களின் தளத்திற்குச் செங்குத்துத் திசையில் இருக்கும். (படம் 2.22)

மற்றும் என்ற இரண்டு வெக்டர்களின், வெக்டர் பெருக்கலினால் கிடைக்கும் தொகுப்பயன் வெக்டர் ஐ கீழ்க்கண்டவாறு குறிப்பிடலாம்.

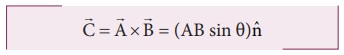
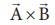இன் அலகு வெக்டர் ன் திசை, அதாவது இன் திசை, மற்றும் வெக்டர்களினாலான தளத்திற்குச் செங்குத்தாக இருக்கும். மேலும் வலதுகை திருகு ஒன்றை வெக்டரில் இருந்து (முதல் வெக்டர்) வெக்டரை நோக்கி (இரண்டாவது வெக்டர்) அவற்றின் சிறிய கோணத்தின் வழியே சுழற்றும் போது திருகு முன்னேறும் திசையில் வெக்டரின் திசை இருக்கும். இது படம் 2.22 இல் காட்டப்பட்டுள்ளது.

வெக்டர் பெருக்கலின் (குறுக்குப் பெருக்கல்) 

பண்புகள் 

(i) இரண்டு வெக்டர்களின், வெக்டர் பெருக்கல் மற்றொரு வெக்டரையே தரும். அவ்வெக்டரின் திசை, அவ்விரண்டு வெக்டர்களினாலான தளத்திற்குச் செங்குத்தாக இருக்கும். மேலும் மற்றும் வெக்டர்கள் ஒன்றுக்கொன்று செங்குத்தாக இருந்தாலும், இல்லையென்றாலும் தொகுபயன் வெக்டர் இவ்விரண்டு வெக்டர்களுக்கும் செங்குத்தாக இருக்கும். 

(ii) இரண்டு வெக்டர்களின் வெக்டர் பெருக்கல் பரிமாற்று விதிக்கு உட்படாது அதாவது

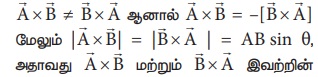
எண்மதிப்புகள் சமம். ஆனால் இவையிரண்டும் எதிரெதிர்திசையில் செயல்படும். 

(iii) இரண்டு வெக்டர்களின் வெக்டர் பெருக்கல் sin θ = 1 என்ற நிபந்தனையில் (θ = 90°) பெரும் மதிப்பைப் பெறும். அதாவது கொடுக்கப்பட்ட வெக்டர்கள் செங்குத்து வெக்டர்கள் எனில் வெக்டர் பெருக்கல் பெரும் மதிப்பைப் பெரும்.

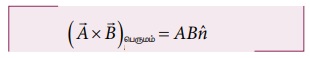
(iv) இரண்டு சுழியற்ற வெக்டர்களின், வெக்டர் பெருக்கல் sin θ = 0, என்ற நிபந்தனையில் (θ = 0° அல்லது 180°) சிறும மதிப்பைப் பெறும்.

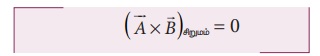
அதாவது கொடுக்கப்பட்ட வெக்டர்கள், ஒன்றுக்கொன்று இணையாகவோ அல்லது எதிராகவோ உள்ள போது, அவற்றின் வெக்டர் பெருக்கல் பலன் சுழியாகும்.

(v) தற்சார்பு வெக்டர் பெருக்கல் அதாவது ஒரு வெக்டரை அதே வெக்டருடன் குறுக்கு பெருக்கல் செய்யும்போது அது சுழிமதிப்பைப் பெறும். அதனை சுழிவெக்டர் என்று அழைக்கலாம்.

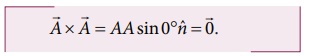
இயற்பியலில் சுழி வெக்டர் எளிமையாக சுழி என்றே குறிக்கப்படுகிறது. 

(vi) ஓரலகு வெக்டர்களின் தற்சார்பு வெக்டர் பெருக்கலும் சுழியாகும்.

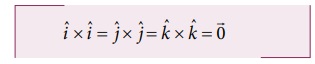
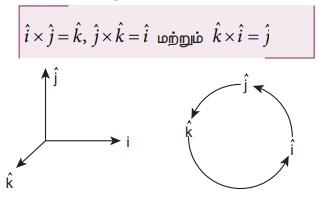
(vii) வலதுகை திருகு விதியின்படி, செங்குத்து ஓரலகு வெக்டர்களின் வெக்டர் பெருக்கல் கீழ்க்கண்டவாறு காணப்படும்.

மேலும், வெக்டர் பெருக்கல் பரிமாற்று விதிக்கு உட்படாததால், கீழ்க்காணுமாறு எழுதலாம்.

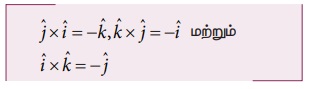
(viii) வெக்டர் கூறு முறையில் இரண்டு வெக்டர்களின் வெக்டர் பெருக்கலை கீழ்க்கண்டவாறு கண்டறியலாம்.

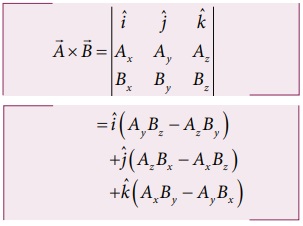
குறிப்பு: கூறின் பெருக்கலின் வரிசையானது கூறு மற்றும் கூறுகளின் பெருக்கலின் வரிசையிலிருந்து மாறுபட்டு உள்ளதைக் கவனிக்கவும். 

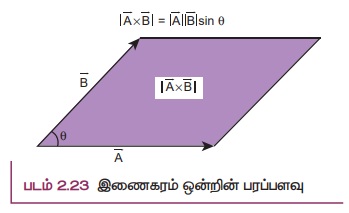
(ix) மற்றும் என்ற இரண்டு வெக்டர்களை இணைகரம் ஒன்றின் அடுத்தடுத்த பக்கங்களாகக் கருதினால், 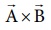- இன் எண்மதிப்பு 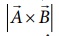அவ்விணைகரத்தின் பரப்பளவைக் கொடுக்கும். இதனை படம் 2.23 காட்டுகிறது.

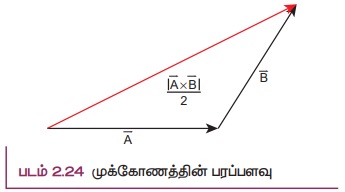
ஒரு இணைகரத்தை நாம் இரண்டு சம அளவுள்ள முக்கோணமாகப் பிரிக்க முடியும் வெக்டர் மற்றும் இருபக்கமாகக் கொண்ட ஒரு முக்கோணத்தின் பரப்பளவு என்பது 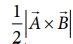க்குச் சமமாக இருக்கும். இது படம் 2.24-யில் காட்டப்பட்டுள்ளது. [இந்த வழிமுறை அலகு - 6 இல் கெப்ளரின் விதிகளைப் பயிலும் போது பயன்படுத்தப்படவிருக்கிறது என்பதை மனதிற் கொள்க].

இயற்பியலில் பயன்படுத்தப்படும் பல்வேறு அளவுகள் வெக்டர் பெருக்கலின் வாயிலாக வரையறை செய்யப்படுகின்றன. குறிப்பாகச் சுழற்சியின் விளைவுகளை, எடுத்துக்காட்டும் திருப்புவிசை, கோண உந்தம் போன்ற அளவுகளை வரையறை செய்யும் போது வெக்டர் பெருக்கல் பயன்படுகிறது.

எடுத்துக்காட்டுகள் 

(i) திருப்பு விசை 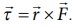இங்கு என்பது விசை மற்றும் என்பது பொருளின் நிலைவெக்டர் ஆகும். 

(ii) கோண உந்தம்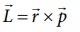

இங்கு என்பது நேர்க்கோட்டு உந்தமாகும். 

(iii) நேர்க்கோட்டுத் திசை வேகம் 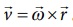இங்குஎன்பது கோணத்திசைவேகமாகும்.

வெக்டர் கூறுகளின் பண்புகள் 

இரண்டு வெக்டர்கள் மற்றும் ஆகியவை ஒன்றுக்கொன்று சமமாக இருப்பின், அவற்றின் கூறுகளும் ஒன்றுக்கொன்று சமமாக இருக்கும்.

வெக்டர்களின் ஸ்கேலர் பெருக்கல் தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள்

இரண்டு வெக்டர்களின் ஸ்கேலர் பெருக்கல் தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள்

ஒரு ஸ்கேலரால் வெக்டரைப் பெருக்குதல் தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள்

வெக்டர் கூறுகள் தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள்