முக்கோணத்தின் பரப்பு

முக்கோணத்தின் பரப்பு (Area of a Triangle)

முக்கோணத்தின் அடிப்பக்கம் மற்றும் உயரம் (குத்துயரம்) கொடுக்கப்பட்டால் அதன் பரப்பைக் காணும் முறையை முந்தைய வகுப்புகளில் கற்றுள்ளோம்.

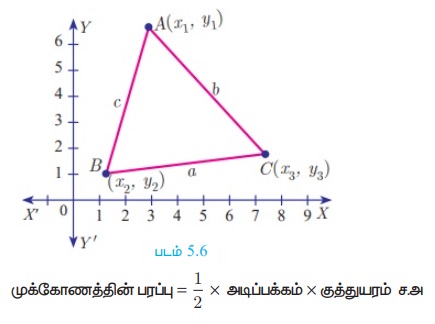
என்ற சூத்திரத்தைப் பயன்படுத்தினோம். ஒரு கோட்டில் அமையாத புள்ளிகளான A(x1 , y1) , B (x2 , y2 ) மற்றும் C (x3 , y3 )-ஐக் கொண்டு ABC என்ற முக்கோணத்தை அமைக்கலாம்.

a, b, c என்பன முக்கோணம் ABC-யின் பக்கங்களின் நீளங்கள் என்க. இங்கு, இரு புள்ளிகளுக்கு இடைப்பட்ட தொலைவைக் காணும் சூத்திரத்தைப் பயன்படுத்தி AB = c, BC = a, CA = b ஆகியவற்றைக் கணக்கிடுகிறோம்.

2s = a +b +c, எனக் கொண்டு, 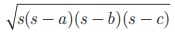எனும் ஹெரோன்ஸ் சூத்திரத்தைப் பயன்படுத்தி முக்கோணம் ABC-யின் பரப்பளவைக் காணலாம். இம்முறையில் முக்கோணத்தின் பரப்பு காண்பது சற்று கடினமாகும்.

மூன்று முனைப் புள்ளிகளைப் பயன்படுத்தி முக்கோணத்தின் பரப்பினைக் (அதன் பக்க அளவுகள் இல்லாமல்) கணக்கிடும் நேர்த்தியான முறையைப் பற்றி இங்கு விவாதிப்போம்.

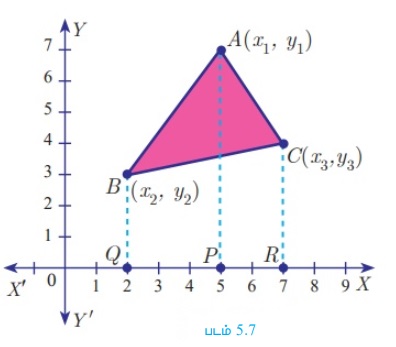
A(x1 , y1) , B (x2 , y2 ) மற்றும் C (x3 , y3 ) என்பன முக்கோணம் ABC-யின் முனைப் புள்ளிகள் என்க. புள்ளிகள் A, B, C-லிருந்து X அச்சுக்குச் செங்குத்தாக முறையே AP, BQ மற்றும் CR வரைக. ABQP, APRC மற்றும் BQRC ஆகியவை சரிவகங்கள் ஆகும்.

இப்பொழுது படம் 5.7-லிருந்து, முக்கோணம் ABC -யின் பரப்பு = சரிவகம் ABQP-யின் பரப்பு + சரிவகம் APRC -யின் பரப்பு சரிவகம்- BQRC -யின் பரப்பு. 

சரிவகத்தின் பரப்பு = 1/2 × (இணைப் பக்கங்களின் கூடுதல்) × (இணைப் பக்கங்களுக்கு இடைப்பட்ட குத்துயரம்)

எனவே, ΔABC -யின் பரப்பு

= 1/2 (BQ + AP) QP + 1/2 (AP + CR) PR − 1/2 (BQ +CR) QR

= 1/2 (y2 + y1) (x1 − x2) + 1/2 (y1 + y3) (x3 − x1) − 1/2 (y2 + y3) (x3 − x2)

= 1/2 {x1 (y2 − y3) + x2(y3 − y1) + x3 (y1 − y2)}

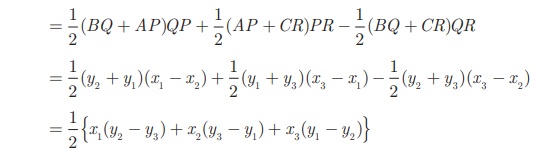
இதிலிருந்து, ΔABC யின் பரப்பானது கீழ்க்காணும் கோவையின் மிகை மதிப்பாகும்.

= 1/2 {x 1 (y 2 − y 3) + x 2(y 3 − y1) + x 3 (y 1 − y2)} சதுர அலகுகள் 

புள்ளிகள் A,B,C-ஐ கடிகாரத்தின் எதிர் திசையில் எடுத்துக்கொண்டால், ΔABC-யின் முனைகள் A(x1 , y1) , B (x2 , y2 ) மற்றும் C (x3 , y3 ) என்பவை "வரிசையாக எடுக்கப்பட்டவை" எனலாம். இவ்வாறு வரிசையாக எடுக்கப்பட்டால் முக்கோணத்தின் பரப்பு எப்பொழுதும் குறை எண்ணாக அமையாது.

மற்றொரு வடிவம்

கீழ்க்கண்ட பட விளக்கமானது மேற்கண்ட சூத்திரத்தை மிக எளிதாகப் பெறுவதற்கு உதவிகரமாக இருக்கும்.

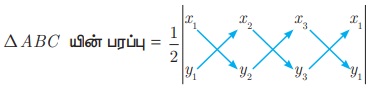
ΔABC யின் பரப்பு = 1/2 {(x1 y2 + x 2 y3 + x 3 y1) − (x 2 y1 + x 3 y2 + x 1y3)} சதுர அலகுகள். 

குறிப்பு

முக்கோணத்தின் பரப்பு குறை எண்ணாக இருக்க இயலாது. எனவே குறை எண்ணாக இருந்தால் அதனை மிகை எண்ணாக எடுத்துக்கொள்ள வேண்டும்.

முன்னேற்றச் சோதனை 

P (0, - 4), Q (3, 1) மற்றும் R(-8, 1) என்பன ΔPQR -யின் முனைப் புள்ளிகள் எனில் 

1. வரைபடத்தாளில் ΔPQR -ஐ வரைக 

2. ΔPQR ஆனது சம பக்கம் உடையதா எனச் சோதிக்க.

3. ΔPQR -யின் பரப்பைக் காண்க. 

4. QP -யின் மையம் M -யின் ஆயப் புள்ளிகளைக் காண்க. 

5. QR யின் மையம் N-யின் ஆயப் புள்ளிகளைக் காண்க. 

6. ΔMPN -யின் பரப்பைக் காண்க.

7. ΔMPN மற்றும் ΔPQR -யின் பரப்புகளின் விகிதம் என்ன? 

ஒரு கோடமைந்த மூன்று புள்ளிகள் (Collinearity of three points)

A(x1 , y1) , B (x2 , y2 ) மற்றும் C (y3 , y3 ) என்ற வெவ்வேறான மூன்று புள்ளிகள் ஒரு கோடமைந்ததாக இருந்தால் அவைகள் ஒரு முக்கோணத்தை அமைக்காது. ஏனெனில் இம்முக்கோணத்திற்குக் குத்துயரம் (உயரம்) இல்லை. எனவே A (x1, y1), B (x2, y2 ) மற்றும் C (x3, y3 ) என்ற மூன்று புள்ளிகள் ஒரு கோடமைந்தவை எனில், ΔABC -யின் பரப்பு = 0.

இதுபோல, ΔABC -யின் பரப்பு பூச்சியம் எனில், கொடுக்கப்பட்ட மூன்று புள்ளிகள் ஒரே நேர்க்கோட்டில் அமையும்.

இதிலிருந்து A (x1, y1), B (x2, y2) மற்றும் C (x3, y3) என்ற மூன்று வெவ்வேறு புள்ளிகள் ஒரு கோடமைந்தவையாக இருந்தால், இருந்தால் மட்டுமே ΔABC -யின் பரப்பு = 0