நேர்க்கோட்டு சமன்பாட்டின் பொது வடிவம்

நேர்க்கோட்டு சமன்பாட்டின் பொது வடிவம் (General Form of a Straight Line)

x, y என்ற இரு மாறிகளில் அமைந்த ஒருபடி பல்லுறுப்புக் கோவை ax + by +c = 0 -ஐ ஒரு நேரிய சமன்பாடு என அழைக்கலாம் (a, b, c என்பன மெய்யெண்கள் மற்றும் a, b -யில் ஏதேனும் ஒன்று பூச்சியமற்றது). இதுவே நேர்க்கோட்டு சமன்பாட்டின் பொது வடிவமாகும். இப்பொழுது கீழ்க்கண்ட தகவல்களுக்கு ஏற்ற நேர்க்கோட்டின் சமன்பாட்டைக் காண்போம்.

(i) ax + by + c = 0 -க்கு இணையான கோடு 

(ii) ax + by + c = 0 - க்கு செங்குத்தான கோடு

1. ax + by + c = 0 என்ற கோட்டிற்கு இணையான நேர்க்கோட்டின் சமன்பாடு (Equation of a line parallel to the line ax + by + c = 0)

ax + by + c = 0 என்ற நேர்க்கோட்டிற்கு இணையாக உள்ள கோடுகளின் சமன்பாடு ax + by + k = 0 ஆகும். இங்கு k-ன் மதிப்பு வெவ்வேறு மதிப்புகளைக் கொண்டிருக்கலாம். 

2. ax + by + c = 0 என்ற கோட்டிற்குச் செங்குத்தான நேர்க்கோட்டின் சமன்பாடு (Equation of a line perpendicular to the line ax + by + c = 0)

ax + by + c = 0 என்ற கோட்டிற்குச் செங்குத்தாக உள்ள கோடுகளின் சமன்பாடு bx - ay + k = 0 ஆகும். இங்கு k-ன் மதிப்பு வெவ்வேறு மதிப்புகளைக் கொண்டிருக்கலாம்.

உங்களுக்குத் தெரியுமா?

a1x + b1y + c1 = 0 மற்றும் a2x + b2y + c2 = 0 என்ற இரு நேர்க்கோட்டுச் சமன்பாடுகளின் கெழுக்கள் பூச்சியமற்றவை எனில், அந்த நேர்க்கோடுகள் 

(i) இணை என இருந்தால், இருந்தால் மட்டுமே a1 / a2 = b1/ b2 அதாவது, a1 b2 – a2b1, = 0

(ii) செங்குத்து என இருந்தால், இருந்தால் மட்டுமே a1a2 + b1b2 = 0.

முன்னேற்றச் சோதனை

விடுபட்ட கட்டங்களைப் பூர்த்தி செய்க

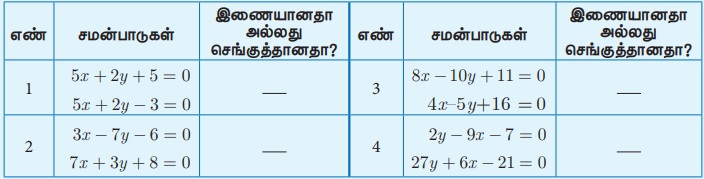
3. நேர்க்கோட்டின் சாய்வு (Slope of a straight line)

ax + by +c = 0 என்பது நேர்க்கோட்டு சமன்பாட்டின் பொது வடிவம் ஆகும். (a, b-யில் ஏதேனும் ஒன்றாவது பூச்சியம் அற்றது)

x-யின் கெழு = a, y-யின் கெழு = b, மாறிலி = c, 

மேலே உள்ள சமன்பாட்டை by = - ax - c என மாற்றி எழுதலாம் 

எனவே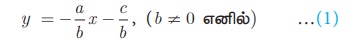  

(1) ஐ y = mx +l உடன் ஒப்பிட 

சாய்வு m = − a/b 

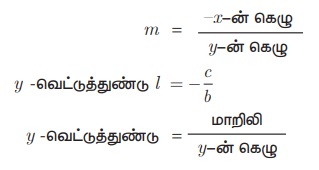
சிந்தனைக்களம் 

சாய்வு 1 என இருக்குமாறு எத்தனை நேர்க்கோடுகள் இருக்கும்? 

எடுத்துக்காட்டு 5.30 

6x + 8y + 7 = 0 என்ற நேர்க்கோட்டின் சாய்வைக் காண்க. 

தீர்வு 

கொடுக்கப்பட்ட நேர்க்கோட்டின் சமன்பாடு 6x + 8y + 7 = 0

எனவே நேர்க்கோட்டின் சாய்வு -3/4 ஆகும். 

எடுத்துக்காட்டு 5.31 

(i) 3x − 7y = 11 -க்கு இணையான (ii) 2x − 3y + 8 = 0 -க்கு செங்குத்தான நேர்க்கோட்டின் சாய்வைக் காண்க. 

தீர்வு 

(i) கொடுக்கப்பட்ட நேர்க்கோட்டின் சமன்பாடு 3x − 7y = 11

3x − 7y − 11 = 0

சாய்வு m = − 3/-7 = 3/7

இணை கோடுகளின் சாய்வுகள் சமம் என்பதால் 3x − 7y = 11 என்ற நேர்க்கோட்டிற்கு இணையான கோட்டின் சாய்வு 3/7 ஆகும். 

(ii) கொடுக்கப்பட்ட நேர்க்கோட்டின் சமன்பாடு 2x − 3y + 8 = 0 

சாய்வு m = −2/−3  = 2/3

ஒன்றுக்கொன்று செங்குத்தான நேர்க்கோட்டு சாய்வுகளின் பெருக்கற்பலன் - 1 என்பதால் 2x − 3y + 8 = 0 என்ற நேர்க்கோட்டிற்குச் செங்குத்தான கோட்டின் சாய்வு =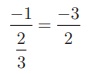

எடுத்துக்காட்டு 5.32 

2x + 3y − 8 = 0, 4x + 6y + 18 = 0 ஆகிய நேர்க்கோடுகள் இணை எனக் காட்டுக. 

தீர்வு 

2x + 3y − 8 = 0 என்ற நேர்க்கோட்டின் சாய்வு

m1 = − 2/3

4x + 6y + 18 = 0 என்ற நேர்க்கோட்டின் சாய்வு

m2 = −4/6 = −2/3

இங்கு, m1   = m2

அதாவது, சாய்வுகள் சமம். எனவே இவ்விரு நேர்க்கோடுகளும் இணையாகும்.

எடுத்துக்காட்டு 5.33 

x − 2y + 3 = 0, 6x + 3y + 8 = 0 ஆகிய நேர்க்கோடுகள் ஒன்றுக்கொன்று செங்குத்தானவை எனக் காட்டுக. 

தீர்வு 

x − 2y + 3 = 0 என்ற நேர்க்கோட்டின் சாய்வு

m1 = −1/−2 = 1/2

6x + 3y + 8 = 0 என்ற நேர்க்கோட்டின் சாய்வு

m2 = −6/3 = −2

இங்கு, m1 × m2  = 1/2 × (−2) = −1

சாய்வுகளின் பெருக்கற்பலன் -1 ஆகும்.

ஆகவே, இவ்விரு நேர்க்கோடுகள் ஒன்றுக்கொன்று செங்குத்தானவையாகும்.

மாற்று முறை

a1 = 1, b1 = -2;

a2 = 6, b2 = 3 a1 a2 + b1 b2 = 6 - 6 = 0

ஆகவே, நேர்க்கோடுகள் செங்குத்தானவையாகும். 

எடுத்துக்காட்டு 5.34 

3x − 7y = 12 என்ற நேர்க்கோட்டிற்கு இணையாகவும் (6,4) என்ற புள்ளிவழிச் செல்வதுமான நேர்க்கோட்டின் சமன்பாட்டைக் காண்க. 

தீர்வு 

3x − 7y = 12 = 0 என்ற நேர்க்கோட்டிற்கு இணையான நேர்க்கோட்டின் சமன்பாடு 3x − 7y + k = 0 

இந்த நேர்க்கோடானது (6,4) என்ற புள்ளி வழிச் செல்வதால்,

3(6) - 7(4) + k = 0

k = 28 - 18 = 10

எனவே, தேவையான நேர்க்கோட்டின் சமன்பாடு 3x − 7y + 10 = 0.

எடுத்துக்காட்டு 5.35 

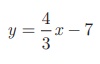என்ற நேர்க்கோட்டிற்குச் செங்குத்தானதும், (7, -1) என்ற புள்ளிவழிச் செல்லுவதுமான நேர்க்கோட்டின் சமன்பாட்டைக் காண்க.

தீர்வு 

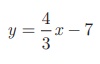என்ற நேர்க்கோட்டின் சமன்பாட்டை 4x − 3y − 21 = 0 என மாற்றி எழுதலாம்.

4x − 3y − 21 = 0 என்ற நேர்க்கோட்டிற்குச் செங்குத்தான நேர்க்கோட்டின் சமன்பாடு 3x + 4y + k = 0

இது (7, -1) என்ற புள்ளி வழிச் செல்வதால் 21 − 4 + k = 0 ⇒ k = −17

ஆகவே, தேவையான நேர்க்கோட்டின் சமன்பாடு 3x + 4y -17 = 0 ஆகும்.

எடுத்துக்காட்டு 5.36 

4x + 5y = 13, x − 8y + 9 = 0 ஆகிய நேர்க்கோடுகள் சந்திக்கும் புள்ளி வழியாகவும், Y- அச்சுக்கு இணையாகவும் உள்ள நேர்க்கோட்டின் சமன்பாட்டைக் காண்க. 

தீர்வு 

கொடுக்கப்பட்ட நேர்க்கோடுகள் 4x + 5y −13= 0   ...(1)

x − 8y + 9 = 0                        ...(2) 

(1) மற்றும் (2) - ஐ தீர்ப்பதின் மூலம் இக்கோடுகள் சந்திக்கும் புள்ளியைக் காணலாம்.

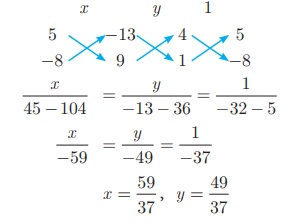
எனவே, இரு நேர்க்கோடுகள் வெட்டிக்கொள்ளும் புள்ளி (x, y) =

Y-அச்சுக்கு இணையான நேர்க்கோட்டின் சமன்பாடு x = c.

இக்கோடானது (x, y) = வழிச் செல்கிறது. எனவே, c = 59/37

நேர்க்கோட்டின் சமன்பாடு x = 59/37. எனவே, 37x − 59 = 0. 

எடுத்துக்காட்டு 5.37 

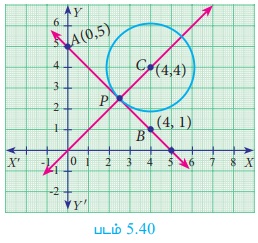
A(0, 5) மற்றும் B(4,1) ஆகிய புள்ளிகளை இணைக்கும் கோடானது C(4,4) - ஐ மையமாகக் கொண்ட வட்டத்தின் தொடுகோடு எனில்,

(i) AB என்ற கோட்டின் சமன்பாட்டைக் காண்க. 

(ii) C வழியாகவும் AB என்ற கோட்டிற்குச் செங்குத்தாக உள்ள நேர்க்கோட்டின் சமன்பாட்டைக் காண்க. 

(iii) AB என்ற கோடானது வட்டத்தைத் தொடும் புள்ளியைக் காண்க. 

தீர்வு 

(i) A(0, 5) மற்றும் B(4,1) என்ற புள்ளிகள் வழிச் செல்லும் AB என்ற கோட்டின் சமன்பாடு 

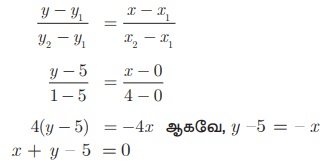
(ii) AB -என்ற கோட்டின் சமன்பாடு x + y − 5 = 0 இந்த நேர்க்கோட்டிற்குச் செங்குத்தான கோட்டின் சமன்பாடு x − y + k = 0 ஆகும். 

இக்கோடானது மையம் (4,4) என்ற புள்ளி வழிச் செல்வதால், 4 - 4 + k = 0 எனவே, k = 0 

C வழியாக AB -க்கு செங்குத்தாக அமையும் நேர்க்கோட்டின் சமன்பாடு x − y = 0  

(iii) x + y - 5 = 0 மற்றும் x – y = 0 ஆகிய நேர்க்கோடுகள்

சந்திக்கும் புள்ளியே AB என்ற கோடானது வட்டத்தைத்

தொடும் புள்ளி ஆகும்.

x + y − 5 = 0 மற்றும் x − y = 0 இவற்றைத் தீர்ப்பதின் மூலம்,

x = 5/2 மற்றும் y = 5/2 

எனவே, தொடுபுள்ளி P-யின் ஆயப் புள்ளிகள் (5/2,5/2) ஆகும்.

சிந்தனைக்களம் 

1. இரு நேர்க்கோடுகள் வெட்டிக்கொள்ளும் புள்ளிகளின் எண்ணிக்கையைக் காண்க.

2. 2x – 3y + 6 = 0 என்ற நேர்க்கோட்டிற்குச் செங்குத்தாக அமையும் கோடுகளின் எண்ணிக்கையைக் காண்க.

செயல்பாடு 6 

கொடுக்கப்பட்ட வரைபடங்களில் உள்ள நேர்க்கோடுகளின் சமன்பாட்டைக் காண்க.