திண்மங்களை கனஅளவுகள் மாறாமல் மற்றொரு உருவத்திற்கு மாற்றி அமைத்தல்

திண்மங்களை கனஅளவுகள் மாறாமல் மற்றொரு உருவத்திற்கு மாற்றி அமைத்தல் (Conversion of Solids from one shape to another with no change in Volume)

உருமாற்றம் அல்லது மாற்றத்தை நாம் அன்றாட வாழ்வில் பல சூழ்நிலைகளில் சந்திக்கின்றோம். எடுத்துக்காட்டாக, ஒரு பொற்கொல்லர் தங்க வில்லைகளை உருக்கி அணிகலன்களாக மாற்றுகிறார். ஒரு குழந்தை களிமண்ணைப் பல பொம்மைகளாக உருவாக்குகிறது. தச்சர் மரத்துண்டுகளைப் பல வீட்டு உபயோகப் பொருட்களாக உருமாற்றுகிறார். இதுபோல ஓர் உருவத்தை மற்றோர் உருவமாக மாற்றும் கருத்தானது பல்வேறு வகைகளில் நமக்குத் தேவைப்படுகிறது.

இந்தப் பகுதியில் மாறாக் கனஅளவுகளுடன் ஓர் உருவத்தை மற்றொரு உருவமாக மாற்றுவது பற்றிக் காண்போம்.

எடுத்துக்காட்டு 7.29

16 செ.மீ ஆரமுள்ள ஓர் உலோகப் பந்து, உருக்கப்பட்டு 2 செ.மீ ஆரமுள்ள சிறு பந்துகளாக்கப்பட்டால், எத்தனை பந்துகள் கிடைக்கும்? 

தீர்வு 

சிறிய உலோகப் பந்துகளின் எண்ணிக்கை n என்க.

சிறிய மற்றும் பெரிய உலோகப் பந்துகளின் ஆரங்கள் முறையே r மற்றும் R என்க.

இங்கு, R = 16 செ.மீ, r = 2 செ.மீ. 

தற்போது, n × (ஒரு சிறிய உலோகப் பந்தின் கனஅளவு) = பெரிய உலோகப் பந்தின் கனஅளவு

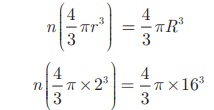
8n = 4096 எனவே n = 512 

ஆகவே, சிறிய உலோகப் பந்துகளின் எண்ணிக்கை 512 ஆகும்.

எடுத்துக்காட்டு 7.30 

களிமண் கொண்டு செய்யப்பட்ட 24 செ.மீ உயரமுள்ள ஒரு கூம்பை ஒரு குழந்தை அதே ஆரமுள்ள ஓர் உருளையாக மாற்றுகிறது எனில் உருளையின் உயரம் காண்க. 

தீர்வு 

h1 மற்றும் h2 என்பன முறையே கூம்பு மற்றும் உருளையின் உயரம் என்க. 

r என்பது கூம்பின் ஆரம் என்க.

இங்கு கூம்பின் உயரம் h = 24 செ.மீ, கூம்பு மற்றும் உருளையின் ஆரம் r செ.மீ 

இங்கு, உருளையின் கனஅளவு = கூம்பின் கன அளவு

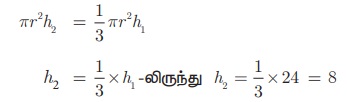
எனவே, உருளையின் உயரம் 8 செ. மீ ஆகும்.

எடுத்துக்காட்டு 7.31 

6 செ.மீ ஆரம் மற்றும் 15 செ.மீ உயரம் கொண்ட ஓர் உருளை வடிவப் பாத்திரம் முழுவதுமாக பனிக்கூழ் (Ice-cream) உள்ளது. அந்தப் பனிக்கூழானது, கூம்பு மற்றும் அரைக்கோளம் இணைந்த வடிவத்தில் நிரப்பப்படுகிறது. கூம்பின் உயரம் 9 செமீ மற்றும் ஆரம் 3 செ.மீ எனில், பாத்திரத்தில் உள்ள பனிக்கூழை நிரப்ப எத்தனைக் கூம்புகள் தேவை?

தீர்வு

h மற்றும் r என்பன முறையே உருளையின் உயரம் மற்றும் ஆரம் என்க.

இங்கு, h = 15 செ.மீ, r = 6 செ.மீ 

உருளையின் கனஅளவு V = πr2h க. அ

= (22/7) × 6 × 6 ×15 

r1 = 3 செ.மீ  மற்றும் h1 = 9 செ.மீ என்பன கூம்பின் ஆரம் மற்றும் உயரம் ஆகும். 

r1 = 3 செ.மீ  என்பது அரைக்காளத்தின் ஆரம் ஆகும். 

பனிக்கூழ்க் கூம்பின் கனஅளவு = கூம்பின் கன அளவு + அரைக்கோளத்தின் கன அளவு

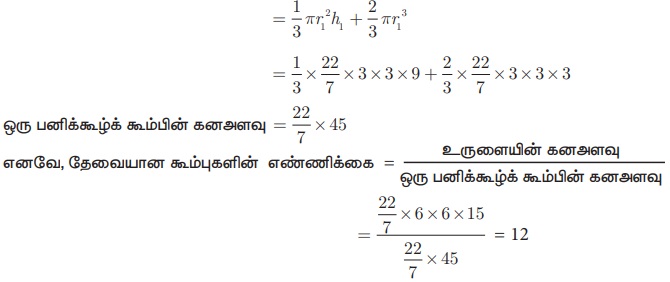
ஆகவே, தேவையான கூம்புகளின் எண்ணிக்கை 12 ஆகும்.

செயல்பாடு 5 

ஓர் உருளையினுள் இருபந்துகள் படத்தில் உள்ளவாறு சரியாகப் பொருந்தியுள்ளன. ஒரு பந்தின் ஆரம் 3 செ.மீ எனில், கீழ்க்கண்டவற்றைக் காண்க.

(i) உருளையின் உயரம் 

(ii) உருளையின் ஆரம் 

(iii) உருளையின் கன அளவு 

(iv) இரு பந்துகளின் கனஅளவு 

(v) பந்துகளால் அடைபடாத உருளையின் கனஅளவு 

(vi) உருளையில் பந்துகளின் கனஅளவின் சதவீதம்