டீ மார்கனின் தேற்றங்கள்

டீ மார்கனின் தேற்றங்கள்

1. டீ மார்கனின் முதல் தேற்றம்

முதல் தேற்றத்தின் கூற்றானது இரு லாஜிக் உள்ளீடுகளின் கூடுதலின் நிரப்பியானது அவற்றின் நிரப்பிகளின் பெருக்கல் பலனுக்குச் சமமாகும்.

நிரூபணம்

NOR கேட்டின் பூலியன் சமன்பாடு வருமாறு

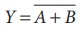
குமிழ் இணைக்கப்பட்ட AND கேட்டுக்கான பூலியன் சமன்பாடு வருமாறு

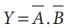
சமமான உள்ளீடுகளுக்கு இரு நேர்வுகளிலும் ஒரே வெளியீடு உருவாகிறது. அதனைக் கீழ்க்காணும் உண்மை அட்டவணையைப் பயன்படுத்தி சரிபார்க்கலாம்.

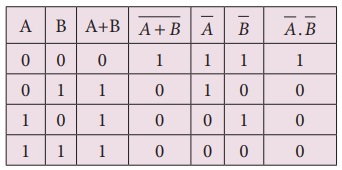
மேற்கண்ட உண்மை அட்டவணையில் இருந்து பின்வரும் முடிவுக்கு வரலாம்.

.

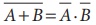ஆகவே டீ மார்கனின் முதல் தேற்றம் நிரூபிக்கப்பட்டது. ஒரு NOR கேட்டானது ஒரு குமிழ் இணைக்கப்பட்ட AND வாயிலுக்குச் சமம் என இது உணர்த்துகிறது.

தொடர்புடைய லாஜிக் சுற்று வரைபடம் படம் 9.47 இல் காட்டப்பட்டுள்ளது

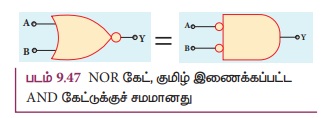
படம் 9.47 NOR கேட், குமிழ் இணைக்கப்பட்ட AND கேட்டுக்குச் சமமானது

2. டீ மார்கனின் இரண்டாம் தேற்றம்

இரண்டாம் தேற்றத்தின் கூற்றானது, இரு உள்ளீடுகளின் பெருக்கல் பலனின் நிரப்பியானது அதன் நிரப்பிகளின் கூடுதலுக்குச் சமமாகும்.

நிரூபணம்

NAND கேட்டுக்கான பூலியன் சமன்பாடு வருமாறு

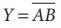
குமிழ் இணைக்கப்பட்ட OR வாயிலுக்கான பூலியன் சமன்பாடு வருமாறு

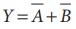
A மற்றும் B உள்ளீடுகள் மற்றும் Y வெளியீடு ஆகும். சமமான உள்ளீடுகளுக்கு மேற்கண்ட இரு சமன்பாடுகளும் ஒரே வெளியீட்டை உருவாக்குகிறது. அதனைப் பின்வரும் உண்மை அட்டவணையைப் பயன்படுத்திச் சரிபார்க்கலாம்.

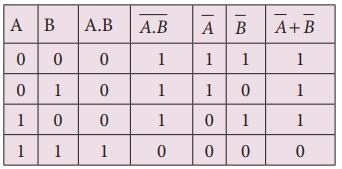
மேற்கண்ட உண்மை அட்டவணையில் இருந்து நாம் பின்வரும் முடிவுக்கு வரலாம்.

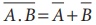
ஆகவே டீ மார்கனின் இரண்டாம் தேற்றம் நிரூபிக்கப்பட்டது. ஒரு NAND கேட்டானது குமிழ் இணைக்கப்பட்ட OR கேட்டுக்குச் சமமானது என அது உணர்த்துகிறது.

தொடர்புடைய லாஜிக் சுற்று வரைபடம் படம் 9.48 இல் காட்டப்பட்டுள்ளது.

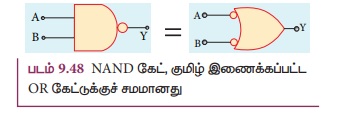
படம் 9.48 NAND கேட், குமிழ் இணைக்கப்பட்ட OR கேட்டுக்குச் சமமானது

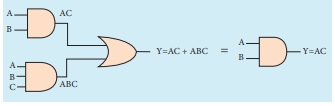
எடுத்துக்காட்டு 9.12

பின்வரும் பூலியன் சமன்பாட்டை எளிமைப்படுத்துக.

AC + ABC = AC

தீர்வு

படி 1: AC (1 + B) = AC.1 (OR விதி - 2)

படி 2: AC. 1 = AC (AND விதி - 2)

எனவே, AC + ABC = AC

சுற்று விளக்கம்