வகை நுண்கணிதம்

வகை நுண்கணிதம் (Differential Calculus)

சார்பு பற்றிய கருத்து (Concept of a function) 

(i) எந்த ஒரு இயற்பியல் அளவும், கணிதவியலின் ஒரு சார்பாக (function) குறிக்கப்படுகிறது. எடுத்துக்காட்டாக வெப்பநிலை T ஐக் கருதுவோம். சுற்றுச்சூழலின் வெப்பம் நாள் முழுவதும் ஒரே சீராக இருப்பதில்லை. அது நண்பகலில் அதிகரிக்கவும், மாலை வேளையில் குறையவும் செய்கிறது.

நாம் கருதும் எந்தவொரு “t” நேரத்திலும் வெப்பநிலை T ஒரு குறிப்பிட்ட மதிப்பினைப் பெற்றிருக்கும். கணிதவிதிகளின் அடிப்படையில் இதனை 'T (t)’ எனக் குறிப்பிடலாம். மேலும் இதனை "நேரத்தைச் சார்ந்த வெப்பநிலை” என அழைக்கலாம். இதிலிருந்து நாம் அறிந்துகொள்வது என்னவெனில், நேரம் ‘t’ கொடுக்கப்பட்டால், அந்த குறிப்பிட்ட நேரத்தில் உள்ள வெப்பநிலையை சார்பு ‘T(t)’ கொடுக்கும். இதேபோன்று x அச்சின் திசையில் செல்லும் பேருந்து ஒன்றின் இயக்கத்தினை x(t) எனக் குறிப்பிடலாம். அதாவது x என்பது நேரத்தைச் சார்ந்த ஒரு சார்பு ஆகும். இங்கு x என்பது அந்த பேருந்தின் ஆய அச்சினைக் குறிக்கிறது.

எடுத்துக்காட்டு 

f(x) = x2 என்ற சார்பைக் கருதுக. சில நேரங்களில் இதனை y = x2 எனவும் குறிப்பிடலாம் இங்கு y என்பது x ஐச் சார்ந்த மாறி, ஆனால் x என்பது சார்பற்ற மாறி ஆகும். x இல் மாற்றம் ஏற்படும் போதெல்லாம் y யிலும் மாற்றம் ஏற்படும் என்பதை இது உணர்த்துகிறது.

இயற்பியல் அளவு ஒன்றினைச் சார்பு வடிவில் குறிப்பிட்ட பின்பு, அந்த சார்பு நேரத்தைப் பொருத்து எவ்வாறு மாறுபடுகிறது (அல்லது) இயற்பியல் அளவு சார்பற்ற மாறிகளைப் பொருத்து எவ்வாறு மாறுபடுகிறது என்பதை அறியலாம். எந்த ஒரு இயற்பியல் அளவில் ஏற்படும் மாற்றத்தையும் பகுத்து ஆராய நுண்க ணிதம் (Calculus) என்ற கணிதவியலின் பிரிவு பயன்படுத்தப்படுகிறது.

y = f(x) என்பது ஒரு சார்பு எனில், x ஐப் பொருத்து y இன் முதல் வகைக்கெழுவை dy/dx எனக் குறிப்பிடலாம். கணிதவியலின்படி y = f(x) என்பது x-இன் பல்வேறு மதிப்புகளுக்கு y - இல் ஏற்படும் மாற்றத்தை எடுத்துக் காட்டுகிறது.

கணித கோட்பாட்டின்படி dy/dx வகைக்கெழு கீழ்க்கண்டவாறு வரையறை செய்யப்படுகிறது.

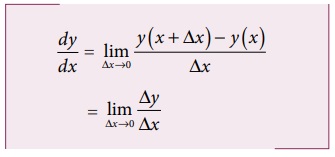
Δx சுழியினை நெருங்கும்போது 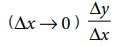அடையும் எல்லையை dy/dx காட்டுகிறது.

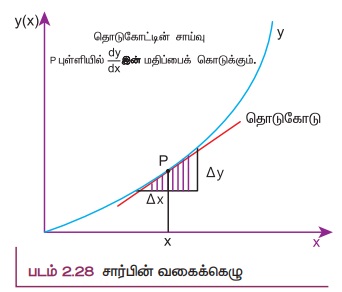
பின்வரும் அட்டவணை இயற்பியலில் பயன்படுத்தப்படும் சில பொதுவான சார்புகளையும், அவற்றின் வகைக் கெழுக்களையும் காட்டுகிறது.

இயற்பியலில், திசைவேகம், வேகம் மற்றும் முடுக்கம் ஆகியவை நேரம் t ஐப் பொருத்த வகைக்கெழுக்கள் ஆகும். அவற்றைப்பற்றி அடுத்த பகுதியில் காணலாம்.

வகை நுண்கணிதம் தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள்

எடுத்துக்காட்டு 2.18 

y = x2 என்ற சார்பினைக் கருதுக. “சார்பு எல்லை” கருத்தைப் பயன்படுத்தி x = 2 என்ற புள்ளியில் அதன் வகைக்கெழு dy/dx ஐக் காண்க.

தீர்வு

x1 = 2 மற்றும் x2 = 3 என்ற இரண்டு புள்ளிகளைக் கருதினால் y1 = 4 மற்றும் y2 = 9 என்ற இரண்டு புள்ளிகள் கிடைக்கும். 

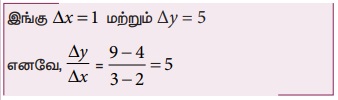
x1 = 2 மற்றும் x2 = 2.5 எனில் y1 = 4 மற்றும் y2 = (2.5)2 = 6.25 எனக் கிடைக்கும் 

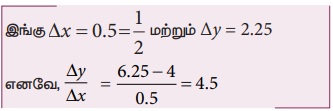
x1 = 2 மற்றும் x2 = 2.25 எனில் y1 = 4 மற்றும் y2 = 5.0625 எனக் கிடைக்கும் 

x1 = 2 மற்றும் x2 = 2.1 எனில் y1 = 4 மற்றும் y2 = 4.41 எனக் கிடைக்கும்.

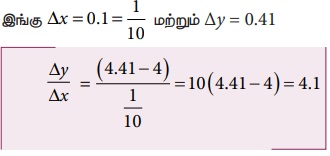
முடிவுகள் கீழ்க்கண்டவாறு அட்டவணைப் படுத்தப்பட்டுள்ளன.

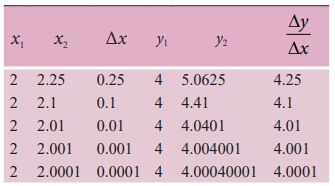
மேற்கண்ட அட்டவணையிலிருந்து பின்வரும் முடிவுகளைப் பெறலாம். 

* Δx சுழியினை நெருங்கும்போது Δy/Δx எண்மதிப்பு 4 என்ற எல்லையை நெருங்குகிறது

* x = 2 என்ற புள்ளியில், வகைக்கெழு 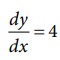ஆகும். 

* மற்றொரு கவனிக்க வேண்டிய அம்சம் என்னவெனில், Δx→0 என்பதை Δx = 0 எனக் கருதக்கூடாது. ஏனெனில் Δx = 0 என்று பிரதியிட்டால் Δy/Δx ஐ வரையறுக்க முடியாது. 

பொதுவாக, சார்பு y = x2 இன் வகைக்கெழுவைக் கீழ்க்கண்டவாறு காணலாம்.

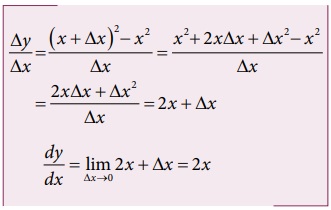
எடுத்துக்காட்டு 2.19 

கொடுக்கப்பட்ட சார்பு x = A0 + A1t + A2 t2 இன் வகைக்கெழுவினை t ஐ பொறுத்துக் காண்க. இங்கு A0, A1, மற்றும் A2, ஆகியவை மாறிலிகள் ஆகும்.

தீர்வு 

இங்கு சார்பற்ற மாறி ‘t’ மற்றும் சார்புடைய மாறி ‘x’ ஆகும். 

நமக்குத் தேவையான வகைக்கெழு

dx/dt = 0+A1+2A2t 

இரண்டாம்படி வகைக்கெழு d2x/d2t = 2A2 ஆகும்.