பின்னங்கள் மற்றும் தசம எண்கள் (Fractions and Decimals)

பின்னங்கள் மற்றும் தசம எண்கள் (Fractions and Decimals)

பின்னங்களுக்கும் தசம எண்களுக்கும் இடையேயான தொடர்பினைக் காணலாம்.

1. பின்னங்களை தசம எண்களாக மாற்றுதல் (Conversion of Fractions to Decimals)

முழுப் பொருளில் ஒரு பகுதியே பின்னம் என்பது நாம் அறிந்ததே. ஓர் எண்ணின் தசம இலக்கங்களின் இடமதிப்புகள் பத்தில் ஒன்றுகள் (1/10), நூறில் ஒன்றுகள் (1/100), ஆயிரத்தில் ஒன்றுகள்,(1/1000) எனத் தொடரும்.

பின்னங்களின் பகுதியானது 10,102,103,... எனில், நாம் அவற்றைத் தசம எண்களாக எழுதலாம். எடுத்துக்காட்டாக, 10 மாணவர்களுக்கு 10 பென்சில்களைக் கொண்ட ஒரு பெட்டியிலிருந்து பகிர்ந்து கொடுப்பதாகக் கருதுக. 6 மாணவர்களுக்குக் கொடுக்கப்பட்ட பென்சில்களின் பின்னமானது 6/10 என்றால் இதனை 0.6 எனக் குறிப்பிடுகிறோம்.

பின்னத்தின் பகுதியானது எந்த எண்ணாக இருந்தாலும், அதனை சமான பின்னத்தைப் பயன்படுத்தி, 10 இன் அடுக்குகளாக மாற்றி அமைத்து தசம எண்களாக குறிப்பிட முடியும். மேலும் ஓர் எடுத்துக்காட்டைக் கருதலாம். 5 நண்பர்கள் வேர்க்கடலை இனிப்பு ஒன்றை 5 சம பாகங்களாக பங்கிட்டுக் கொள்கிறார்கள் எனில், அதில் ஒருவரது பங்கு 1/5. இப்பின்னத்தின் பகுதியைப் பத்தாக மாற்றிட, பின்னத்தைத் தசம எண்ணில் குறிப்பிட முடியும். அதாவது 1/5 ஐ, அதன் சமான பின்னமான 2/10 என எழுதலாம். தற்போது 2/10 இன் தசம எண் வடிவம் 0.2 ஆகும்.

சிந்திக்க

அனைத்து பின்னங்களின் பகுதிகளையும் பத்தின் அடுக்குகளாக உங்களால் மாற்ற இயலுமா?

2. தசம எண்களை பின்னங்களாக மாற்றுதல் (Conversion of Decimals to Fractions)

பின்னங்களைத் தசம எண்களாக மாற்றுவது போல தசம எண்களையும் பின்னங்களாக மாற்ற இயலும்.

எடுத்துக்காட்டாக, பிராண்ட் ‘x’ காலணிகளின் விலை ₹399.95 என்க.

மேலே உள்ள விலையை விரிவுபடுத்த, நமக்குக் கிடைப்பது, 

399.95 = 3 ×100 + 9 ×10 + 9 ×1 + 9 × 1/10 + 5×1/100

= 399 + 95/100 = 39995/100 = 7999/20

இதே போன்று, பிராண்ட் 'y' காலணியின் விலை ₹ 159.95 எனில், இதனைப் பின்னமாகக் கீழ்க்கண்டவாறு குறிப்பிடலாம்.

159.95 = 159 + 95/100 = 15995/100 = 3199/20

இவற்றை முயல்க

1. கீழ்க்காணும் பின்னங்களை தசம எண்களாக மாற்றுக.

 (i) 16 / 1000

(ii) 638/10

(iii) 1/20

(iv) 3/50

(i) 16/1000 = 0.016

(ii) 638 / 10 = 638

(iii) 1/20 × 5/5 = 5/100 = 0.05

(iv) 3/50 × 2/2 = 6/100 = 0.06

2. பின்வருவனவற்றைப் பின்னங்களாக மாற்றுக.

(i) 6 நூறுகள் + 3 பத்துகள் + 3 ஒன்றுகள் + 6 நூறில் ஒன்றுகள் + 3 ஆயிரத்தில் ஒன்றுகள்

(ii) 3 ஆயிரங்கள் + 3 நூறுகள் + 4 பத்துகள் + 9 ஒன்றுகள் + 6 பத்தில் ஒன்றுகள். 

(i) 6 நூறுகள்  + 3 பத்துகள்  + 3 ஒன்றுகள்  + 6 நூறில் ஒன்றுகள்  + 3 ஆயிரத்தில் ஒன்றுகள் . . .

6 × 100 – 3 × 10 + 3 × 1+ 6 × 1/100 + 3 × 1/ 1000

600+ 30 + 3 + 6/100 + 3/1000

633063

(ii) 3 ஆயிரங்கள்  + 3 நூறுகள் + 4 பத்துகள் + 9 ஒன்றுகள் + 6 பத்தில் ஒன்றுகள்.

3 × 1000 + 3 ×  100 + 4 × 10 + 9 × 1+ 6 × 1/10

3000– 300 + 40 + 9 + 6/10

33496

3. கீழ்க்கண்ட தசம எண்களைப் பின்னமாக மாற்றுக.

(i) 0.0005

(ii) 6.24

(i) 0.0005 = 5 / 10000 = 1 / 2000

(ii) 6.24 = 624 / 100 = 156 / 25

எடுத்துக்காட்டு 1.6 

கீழ்க்காணும் படங்களில் உள்ள நிழலிடப்பட்ட பகுதியினைப் பின்னமாகவும் தசம எண்ணாகவும் குறிப்பிடுக.

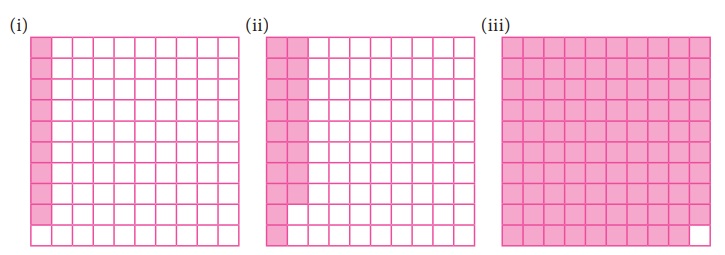
தீர்வு

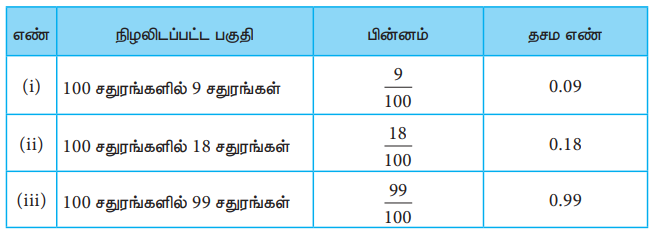
எடுத்துக்காட்டு 1.7 

கீழ்க்காணும் பின்னங்களைத் தசம எண்களாக மாற்றுக.

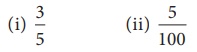
தீர்வு

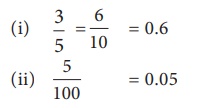
எடுத்துக்காட்டு 1.8 

கீழ்க்காணும் பின்னங்களைத் தசம எண்களாக மாற்றுக.

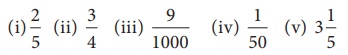
(i) 2/5

(ii) 3/4

(iii) 9/1000

 (iv) 1/50  

(v) 3 1/5

தீர்வு

(i) 2/5 இன் பகுதி 10 ஆக இருக்குமாறு சமான பின்னங்களைக் காணலாம்  

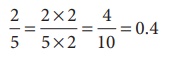
(ii) 3/4 இன் பகுதி 100 ஆக இருக்குமாறு சமான பின்னங்களைக் காணலாம்

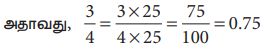
அதாவது, 3/4 = 3×25/4×25 = 75/100 = 0.75 (ஏனெனில் 4 ஆல் பெருக்கினால் 10 வருமாறு முழு எண் இல்லை)

(iii) 9/1000 இல் பத்தில் ஒன்று, நூறில் ஒன்றின் இடமதிப்பு பூஜ்ஜியம் 

எனவே, 9/1000 = 0.009

(iv) 1/50 என்ற பின்னத்திற்குப் பகுதி 100 ஆக இருக்குமாறு சமான பின்னதைக் காணலாம்.

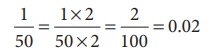
(v) 3 1/5 இல் முழு எண் பகுதி 3, பின்னமான 1/5 இன் பகுதி 10 ஆக இருக்குமாறு சமான பின்னத்தைக் காண

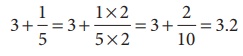
எடுத்துக்காட்டு 1.9 

கீழ்க்கண்டவற்றை எளிய பின்னங்களாக மாற்றுக.

(i) 0.04

(ii) 3.46

(iii) 0.862

தீர்வு

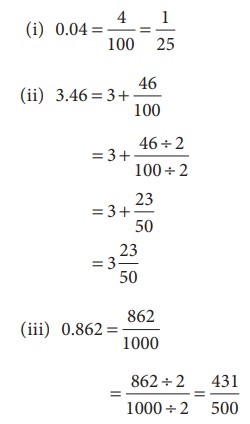
எடுத்துக்காட்டு 1.10 

கீழ்க்கண்ட பின்னங்களைத் தசம வடிவில் எழுதுக. 

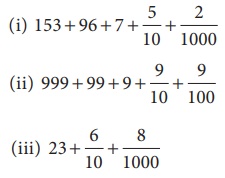
தீர்வு 

= 23.608 (நூறில் ஒன்றிற்கான இலக்கம் இல்லை என்பதால்,  அது '0' என எடுத்துக்கொள்ளப்படுகிறது)

எடுத்துக்காட்டு 1.11 

கீழ்க்கண்டவற்றைத் தசம எண்ணாக எழுதுக.

(i) நானூற்று நான்கு, நூறில் ஐந்து

(ii) இரண்டு, ஆயிரத்தில் இருபத்து ஐந்து 

தீர்வு 

(i) நானூற்று நான்கு, நூறில் ஐந்து

= 404 + 5/100

= 404 +0× 1/10+5×1/100 = 404.05

(ii) இரண்டு , ஆயிரத்தில் இருபத்து ஐந்து

குறிப்பு 

எந்த ஒரு தசம எண்ணிற்கும், பகுதியில் உள்ள பூஜ்ஜியங்களின் எண்ணிக்கையும் தசம இலக்கங்களின் எண்ணிக்கையும் சமமாக இருக்கும்.

எடுத்துக்காட்டு 1.12 

(i) ஒரு மாத்திரையானது 0.85 மி.கி. மருந்தைக் கொண்டுள்ளது. (ii) ஒரு குடுவையில் மாம்பழச் சாறு 4.5 லிட்டராக உள்ளது. இவற்றைப் பின்னத்தில் குறிப்பிடுக.

தீர்வு

தசமம் என்பது ஒரு பின்னம், இது சிறப்பு வடிவில் எழுதப்பட்டிருக்கிறது. தசமம் என்பது  நூறு எனப் பொருள்படும் 'டெசிமஸ்' என்ற இலத்தீன் வார்த்தையிலிருந்து பெறப்படுகிறது. இது 'டெசிம்' என்ற வேர்ச் சொல்லிலிருந்து பெறப்படுகிறது.