எண்ணியல் | இரண்டாம் பருவம் அலகு 1 | 7ஆம் வகுப்பு கணக்கு - தசம எண்களைக் குறித்தல் (Representing a Decimal Number) | 7th Maths : Term 2 Unit 1 : Number System
7ஆம் வகுப்பு கணக்கு : இரண்டாம் பருவம் அலகு 1 : எண்ணியல்
தசம எண்களைக் குறித்தல் (Representing a Decimal Number)
தசம எண்களைக் குறித்தல் (Representing a Decimal Number)
(i) கீழ்க்கண்ட படங்களில் குறிப்பிடப்பட்டுள்ள பத்துகள், ஒன்றுகள் மற்றும் பத்தில் ஒன்றுகளை உற்று நோக்குக.
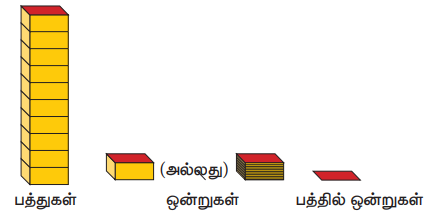
எடுத்துக்காட்டாக, 3.2 என்ற தசம எண்ணைக் கீழ்க்கண்டவாறு படவிளக்க முறையில் குறிப்பிடலாம்.

இது போன்று எந்த ஒரு தசம எண்ணையும் மேல் உள்ள முறையில் குறிப்பிட இயலும்.
இவற்றை முயல்க
கீழ்க்காணும் தசம எண்களைப் படவிளக்கத்தில் குறிக்கவும்.
(i) 5 ஒன்றுகள் 3 பத்தில் ஒன்றுகள்
(ii) 6 பத்தில் ஒன்றுகள்
(iii) 7 ஒன்றுகள் 9 பத்தில் ஒன்றுகள்
(iv) 6 ஒன்றுகள் 4 பத்தில் ஒன்றுகள்
(v) 7 பத்தில் ஒன்றுகள்

எண்களின் இடமதிப்பு பற்றித் தொடக்கநிலை வகுப்பில் நாம் முன்னரே படித்திருக்கிறோம். அதன் தொடர்ச்சியாக தற்போது நாம் தசம எண்களின் இலக்கங்களின் இடமதிப்புக் குறித்துக் கற்போம். எண்களின் விரிமுறையைப் பற்றி நினைவு கூர்வோம்.
3768 என்ற எண்ணைக் கருதுக. 3768 இன் விரிவாக்கம் 3 × 1000 + 7 × 100 + 6 × 10 + 8. இப்பொழுது 235.68 என்ற தசம எண்ணைக் கருதுக.
அதன் விரிவாக்கம், 235.68 = 200 +30 +5+ 6/ 10 + 8/ 100
= 2 × 100+ 3 × 10 + 5 × 1 + 6 × 1/10 + 8 × 1/100
சிந்திக்க
மேற்கண்ட எண்கோவையைப் பத்தின் அடுக்காகப் பின்வருமாறு எழுதலாம். 235.68 = 2 × 102 + 3 × 101 + 5 × 100 + 6 × 10−1 + 8 × 10−2 எனவே, எந்தவொரு எண்ணிலும், ஓர் இலக்கத்திலிருந்து அடுத்த இலக்கத்திற்கு வலப்புறமாக நகரும் பொழுது, இடமதிப்பானது 101-ஆல் வகுக்கப்படுகிறது.
இப்பொழுது, 3768 மற்றும் 25.6 என்ற இரண்டு எண்களை எண் மதிப்புக் கட்டத்தில் (grid) குறிப்பிடலாம்.

இப்பாடப்பகுதியின் தொடக்கத்தில் கவின், கலா என்ற இரு நண்பர்கள் தங்களது பென்சில்களின் நீளம் குறித்து நிகழ்த்திய உரையாடலைப் பற்றிக் கண்டோம். அந்த நீளங்களையும் கீழ்க்கண்டவாறு இடமதிப்புக் கட்டத்தில் குறிப்பிட இயலும்.
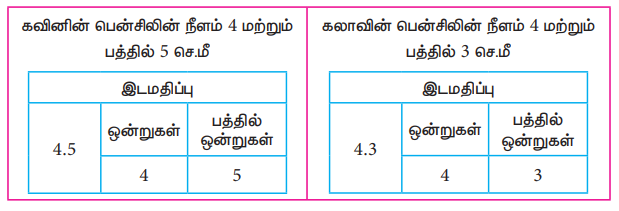
ஒன்றாவது இலக்கத்திற்கு வலப்புறமாக இருப்பது பத்தில் ஒன்றுகள். மேலும் அவற்றிற்கிடையில் உள்ள புள்ளியானது தசமப் புள்ளி ஆகும். அது முழு எண் பகுதியையும் தசமப் பகுதியையும் பிரிக்கின்றது என நாம் அறிகிறோம்.
மேலே கண்ட சூழல்களில் எண்கோவையில் ஒரு தசம இலக்கத்தைக் கொண்ட எண்களை இடமதிப்புக் கட்டத்தில் குறிப்பிட்டுள்ளோம். தற்பொழுது, இரு தசம இலக்கத்தை இடமதிப்புக் கட்டத்தில் குறிக்க, நாம் முன்னரே அறிமுகப் பகுதியில் ஆலோசித்ததைக் கருதுவோம்.
இரவி பொங்கல் பண்டிகைக்கு புத்தாடைகளை வாங்கியிருக்கிறார். அவரது கால் சட்டைத் துணியின் நீளமானது 4 மீ 75 செ.மீ எனக் கொடுக்கப்பட்டுள்ளது. சென்டிமீட்டரில் உள்ளதை மீட்டரில் மாற்ற பின்வருவனவற்றை மேற்கொள்வோம்.
100 செ.மீ = 1 மீ
1 செ.மீ = 1 / 100 மீ
எனவே, ஒரு செ.மீ-ஐ நூறில் ஒரு மீட்டர் எனக் குறிப்பிடலாம்.
இதேபோன்று , 75 செ.மீ = 75 /100 = 0.75 மீ
எனவே கால் சட்டைத் துணியின் நீளம் 4 + 0.75 மீ
அதாவது 4.75 மீ. இதனை நான்கு மற்றும் நூறில் எழுபத்து ஐந்து மீட்டர் (அ) நான்கு புள்ளி ஏழு ஐந்து மீட்டர் எனப் படிக்கலாம்.
குறிப்பு
தசமப் புள்ளிக்குப் பிறகு உள்ள தசம இலக்கங்களைத் தனித் தனியாகப் படிக்க வேண்டும்.
இவற்றை முயல்க
1. கீழ்க்கண்ட தசம எண்களை விரிவாக்க வடிவிலும் இடமதிப்புக் கட்டத்திலும் எழுதுக.
(i) 56.78 (ii) 123.32 (iii)354.56
(i) 56.78
விரிவாக்கப்பட்ட வடிவம் 56.78 = 50+6 + 7/10 + 8/100
= 5 × 10 + 6 × 1 + 7 × 1/10 + 8 ⊂ 1/100
இடமதிப்பு கட்டத்தில்

(ii) 123.32
விரிவாக்கப்பட்ட வடிவம் 123.32 = 100 + 20 + 3 + 3/10 + 2/100
= 1 × 100 + 2 × 10 + 3 × 1 + 3 × 1/10 + 2 ⊂ 1/100
இடமதிப்பு கட்டத்தில்

(iii) 354.56
விரிவாக்கப்பட்ட வடிவம் 354.56 = 300 + 50 + 4 + 5/10 + 6/100
= 3 × 100 + 5 × 10 + 4 × 1 + 5 × 1/10 + 6 ⊂ 1/100
இடமதிப்பு கட்டத்தில்

2. கீழ்க்கண்ட அளவுகளை மீட்டராகவும் தசம எண்ணாகவும் குறிப்பிடுக. எடுத்துக்காட்டிற்கு ஒன்று கொடுக்கப்பட்டுள்ளது.
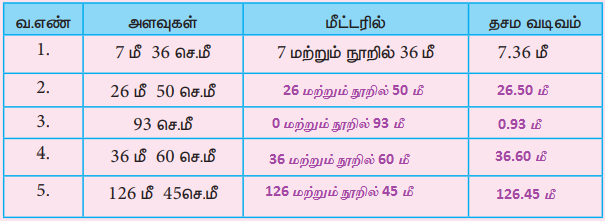
3. கீழ்க்கண்ட எண்களை இடமதிப்புக் கட்டத்தில் குறித்து அடிக்கோடிடப்பட்ட எண்ணின் இடமதிப்பைக் காண்க.
(i) 36.37 (ii) 267.06 (iii) 0.23 (iv) 27.69 (v) 53.27
(i) 36.37
இடமதிப்பு கட்டத்தில்

36.37
36.37 இல் 3ன் இடமதிப்பு பத்தில் ஒன்று
(ii) 267.06
இடமதிப்பு கட்டத்தில்
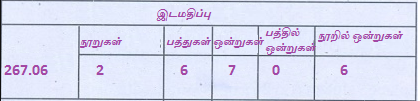
267.0 6
267.06 இல் 6ன் இடமதிப்பு நூறில் ஒன்று
(iii) 0.23
இடமதிப்பு கட்டத்தில்
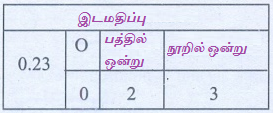
0.2 3
0.23 இல் 6ன் இடமதிப்பு பத்தில் ஒன்று
(iv) 27.69
இடமதிப்பு கட்டத்தில்
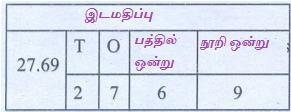
27.69
27.69
(v) 53.27
இடமதிப்பு கட்டத்தில்
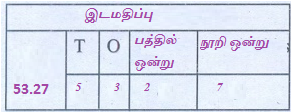
53.27
53.27இல் 2ன் இடமதிப்பு பத்தில் ஒன்று
ஓர் எண்ணில் பத்தில் ஒன்று, நூறில் ஒன்று ஆகிய இடமதிப்புகளை முறையே 1/10, 1/ 100 எனக் குறிப்பதைக் கவனிக்க.
எடுத்துக்காட்டு 1.1 கீழ்க்கண்ட தசம எண்களைப் பட விளக்கத்தில் குறிக்க.
(i) 0.3
(ii) 3.6
(iii) 2.7
(iv) 11.4
தீர்வு
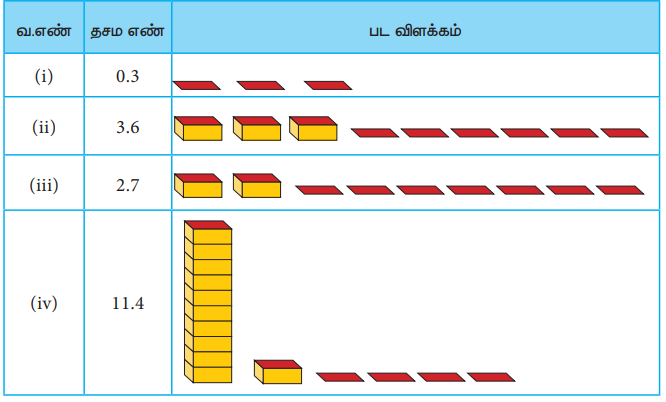
எடுத்துக்காட்டு 1.2
கீழுள்ளவற்றை இடமதிப்புக் கட்டத்தில் எழுதி அடிக்கோடிட்ட இலக்கங்களின் இடமதிப்பைக் காண்க.
(i) 0.37
(ii) 2.73
(iii) 28.271
தீர்வு
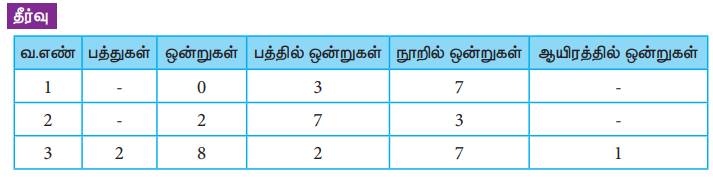
(i) 0.37 இல் 7 இன் இடமதிப்பு நூறில் ஒன்று
(ii) 2.73 இல் 7 இன் இடமதிப்பு பத்தில் ஒன்று
(iii) 28.271 இல் 7 இன் இடமதிப்பு நூறில் ஒன்று
எடுத்துக்காட்டு 1.3
ஒரு மனிதனின் உயரம் 165 செ.மீ. இதனை மீட்டரில் குறிக்க.
தீர்வு
மனிதனின் உயரம் (கொடுக்கப்பட்டுள்ளது) = 165 செ.மீ
எனவே, மனிதனின் உயரம் = 165/100 = 1.65 மீ.
ஏனெனில், 1 செ.மீ = 1/100 மீ = 0.01 மீ
எடுத்துக்காட்டு 1.4
பிரவின் அவனது நண்பர்களுடன் மலை ஏறுவதற்குச் செல்கிறார். அவனது விளையாட்டுப் புத்தகத்தில் அவன் கடந்த தூரத்தினை கிலோமீட்டரில் பதிவு செய்ய விரும்புகிறார். அவனுக்கு உன்னால் உதவ முடியுமா? நான்கு நாள்களுக்கான மலை ஏறிய பதிவுகள் கீழே கொடுக்கப்பட்டுள்ளன?
(i) 4 மீ (ii) 28 மீ (iii) 537 மீ (iv) 3983 மீ
தீர்வு
ஏனெனில், 1 மீ = 1 / 1000 கி.மீ = 0.001 கி.மீ
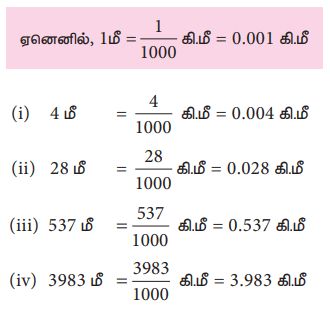
எனவே, பிரவினின் மலை ஏற்றப் பதிவுகள் 0.004 கி.மீ, 0.028 கி.மீ, 0.537 கி.மீ, 3.983 கி.மீ ஆகும்.
எடுத்துக்காட்டு 1.5
கீழே கொடுக்கப்பட்டுள்ள விரிவான வடிவத்தில் உள்ள எண்ணை இடமதிப்புக் கட்டத்தில் குறிப்பிடுக. மேலும் அதனுடைய தசம எண்ணை எழுதுக.
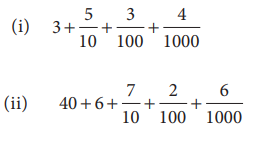
தீர்வு