11 வது கணக்கு : அலகு 11 : தொகை நுண்கணிதம் Integral Calculus
தொகை நுண்கணிதம் Integral Calculus: அறிமுகம் (Introduction)
அத்தியாயம் 11
தொகை நுண்கணிதம் INTEGRAL CALCULUS

"குறியீடுகள் புதிய கண்டுபிடிப்புகளை எளிமையாக்குகின்றன. வியத்தகு வகையில் இவை சிந்தனையை எளிமையாக்குகின்றன” – லிபினிட்ஸ்
அறிமுகம் (Introduction)

காட்ஃபிரைட் வில்ஹெல்ம் லிபினிட்ஸ் (1646-1716) மற்றும் சர் ஐசக் நியூட்டன் (1643-1727) ஆகியோர் 17-ஆம் நூற்றாண்டின் மத்தியில் தனித்தனியாக நுண்கணிதத்தை கண்டுபிடித்தனர். தத்துவஞானி, கணிதவியலாளர், அரசியல் ஆலோசகர், மற்றும் தர்க்கவியலாளர் எனப் போற்றப்பட்ட ஜெர்மானிய நாட்டவரான லிபினிட்ஸ், வகையிடல் மற்றும் தொகையிடல் நுண்கணிதத்தைத் தனித்துவமாக கண்டுபிடித்தார். இதே காலக்கட்டத்தில் இங்கிலாந்து நாட்டைச் சார்ந்த சர் ஐசக் நியூட்டன் ஒரு வளைவரையின் கீழ் உள்ள பரப்பினைக் காண நுண்கணிதத்தின் அடிப்படைத் தேற்றத்தை உருவாக்கினார். நியூட்டன் கணிதத்தோடு நிற்காமல், ஒளியியல் மற்றும் புவிஈர்ப்பு ஆகியவற்றின் கோட்டுபாடுகளையும் உருவாக்கினார்.

வகையிடல் மற்றும் தொகையிடல் இல்லாமல் இவ்வுலகத்தை நம்மால் கற்பனை கூடச் செய்ய இயலாது. கணிதத்தின் வகையிடல் மற்றும் தொகையிடல் ஆகிய இரண்டு அடிப்படைக் கூறுகளின் பயன்பாடுகளால் இந்த நூற்றாண்டில் அறிவியல் வளர்ச்சி குறிப்பிடத்தக்க அளவில் மேம்பட்டு இருப்பதைக் காணலாம். இயற்பியல், வேதியியல், பொறியியல், வானியல், கனிமவியல், உயிரியல் மற்றும் சமூக அறிவியலில் ஏற்படும் பல்வேறு வகையான பிரச்சனைகளின் தீர்வுகளைக்காண்பதற்கு மேற்கூறிய இரண்டு அடிப்படைக் கூறுகளின் பயன்பாடுகள் தவிர்க்க முடியாத ஒன்றாகும். நுண்கணிதம் கொள்கை அளவில் இருவகை வடிவியல் கணக்குகளைப் பற்றியது.
(i) ஒரு வளைவரையின் தொடுகோட்டின் சாய்வினை எல்லை காணும் முறையில் கற்பதை வகையிடல் என்கிறோம்.
(ii) ஒரு வளைவரையின் கீழ் அமைந்துள்ள பகுதியின் பரப்பளவினை எல்லை காணும் முறையில் கற்பதைத் தொகையிடல் என்கிறோம்.
நாம் 9 மற்றும் 10 ஆகிய அத்தியாயங்களில் வகை நுண்கணிதத்தைப் படித்துள்ளோம். இந்த அத்தியாயத்தில் தொகையிடலுக்கான சில அடிப்படை வழிமுறைகளைக் காண்போம்.
கீழே விவரிக்கப்பட்டுள்ள சில எளிமையான நடைமுறைச் சூழ்நிலைகளைக் கொள்வோம்
சூழ்நிலை 1
A மற்றும் Bஎன்ற புள்ளிகளுக்கிடையேயான (படம் 11.1(a)), மீச்சிறு தூரம் அவ்விருபுள்ளிகளை இணைக்கும் நேர்க்கோட்டுத் துண்டாகும். ஒரு துகளானது A யிலிருந்து B-க்கு (செங்குத்தாக அமையாத) வழுக்கிச் செல்லும்போது எடுத்துக்கொள்ளும் மிகக்குறைந்த நேரம் கொண்ட பாதையைக் காண முற்படுவதாகக் கொள்வோம். பெரும்பாலானோர் மீச்சிறு தூரம் கொண்ட AB என்ற நேர்க்கோட்டு வழியாக வந்தால் (படம் 11.1(a)) எடுத்துக்கொள்ளும் நேரம் மீச்சிறு நேரம் என நம்புகின்றனர்.
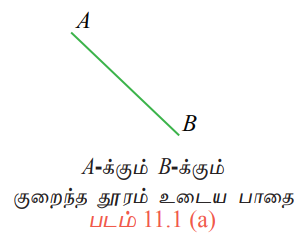
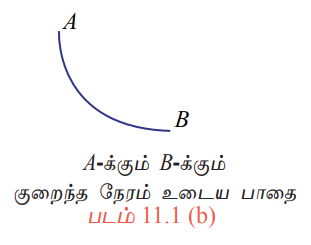
ஆனால், A யையும் Bயையும் இணைக்கும் நேர்க்கோடு மீச்சிறு நேரம் கொண்ட பாதையாக இருக்காது. ஏனெனில் A க்கு அருகில் அதிக சாய்வு கொண்ட வளைவரையில் (படம் 11.1 (b)) இயங்கும் திசைவேகமானது நேர்க் கோட்டில் (படம் 11.1 (a)) இயங்கும் திசைவேகத்தை விட அதிகமாக இருக்கும். இந்த வளைவரையின் பாதை மிக நீளமானதாக இருந்தபோதிலும், இந்தப் பாதையை அதிவேகமாக மிகக்குறைந்த நேரத்தில் கடக்கலாம். நுண்கணிதத்தைப் பயன்படுத்தித் இக்கணக்கிற்கான தீர்வு காணலாம் இது ‘பிராகிஸ்ட்ஸ்டோக்ரோன் (Brachistochrone)' கணக்கு என்று அழைக்கப்படுகிறது.
சூழ்நிலை 2
ஆரம்ப வடிவியலில் அறியப்பட்ட சூத்திரங்களைப் பயன்படுத்திப் பின்வரும் ஒழுங்கான வடிவங்களின் அளவீடுகளைக் காண்பதைப் பற்றி ஏற்கனவே நாம் படித்துள்ளோம்.
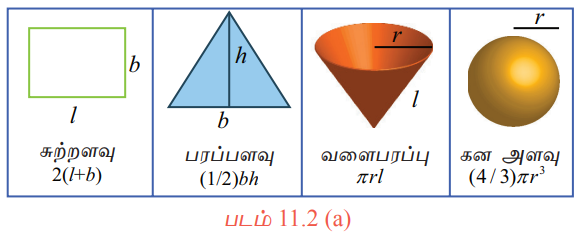
பின்வரும் வரைபடங்களினால் குறிப்பிடப்பட்ட அளவீடுகளை, சார்புகளைக் கொண்டு எவ்வாறு கணக்கிட முடியும்?
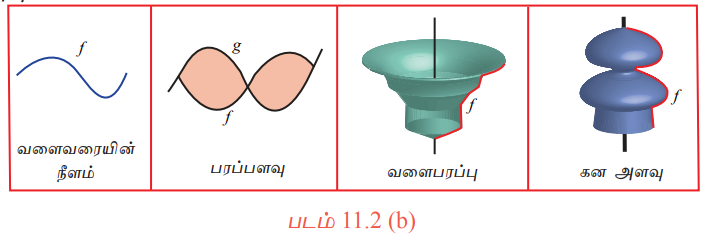
இந்தக் கணக்குகள் காண்பதற்கு கடினமாக இருந்த போதிலும் நுண்கணிதத் தொகையிடல் மூலம் இவற்றை எளிதாக தீர்க்கலாம்.
சூழ்நிலை 3
மாணவர் ஒருவர் தன் மோட்டார் சைக்கிளில் 24 மீ/ வினாடி வேகத்தில் சென்று கொண்டிருக்கும்போது, குறிப்பிட்ட தருணத்தில் தனக்கு முன்பாக 40 மீட்டர் தொலைவில் இருக்கும் தடுப்பின் மீது மோதலைத் தவிர்க்க வாகனத்தை நிறுத்த வேண்டியுள்ளது. உடனடியாகத் தன்னுடைய வாகனத்தை 8 மீ/வினாடி எதிர் முடுக்கத்தில் வேகத்தைக் குறைக்கிறார் எனில் வாகனம் தடுப்பின் மீது மோதுவதற்கு முன் நிற்குமா?

நம் அன்றாட வாழ்கையில் இயற்கையாகவே நிகழும் பல்வேறு நிகழ்வுகளை நாம் பார்ப்போம்.
• எந்த வேகத்தில் மேல் நோக்கி உந்தப்படும் ஒரு செயற்கைகோள் மீண்டும் பூமியை நோக்கித் திரும்பாது?
• கொடுக்கப்பட்டுள்ள சுற்றளவைக் (P) கொண்ட இருசமபக்க முக்கோணத்தை உள்ளடக்கிய சிறிய வட்டத்தகட்டின் ஆரம் எவ்வளவு?
• 2r ஆரம் கொண்ட திண்மக்கோளத்தின்,மையத்திலிருந்து r ஆரம் கொண்ட ஒரு துளையினை உருவாக்கினால் வெளியேற்றப்படும் துகளின் கன அளவு எவ்வளவு?
• கிருமிகளின் வளர்ச்சி விகிதம் அப்போதைய தொகையைப் பொறுத்து மாறுபடுகிறது மற்றும் அதன் வளர்ச்சி ஒரு மணி நேரத்தில் இரு மடங்காகிறது எனில் இரண்டு மணிநேரம் கழித்து அதன் வளர்ச்சி எவ்வளவாக இருக்கும்?
மேற்கூறிய நிகழ்வுகளுக்குத் தொகையிடல் விடையளிக்கிறது.
கற்றலின் நோக்கங்கள்
இப்பாடப்பகுதி நிறைவுறும்போது மாணவர்கள் அறிந்திருக்க வேண்டியவைகளாக
• அறுதியிடப்படாத தொகையிடலின் வரையறையை வகையிடலின் எதிர்ச்செயலாக்கமாக புரிந்துகொள்ளுதல்
• மாறிலியின் மடங்குகள், கூட்டல் மற்றும் கழித்தல் ஆகிய அடிப்படைச் சார்புகளின் அறுதியிடப்படாத தொகையினைக் கண்டறிதல்
• சேர்ப்புச் சார்புகளின் தொகையினைக் காணப் பொருத்தமான வழி முறைகளைப் பயன்படுத்துதல்
• ஒரு சார்பின் மாறுவீதம் கொடுக்கப்பட்டால் அச்சார்பினைத் தொகையிடல் மூலம் காணல் ஆகியவை எதிர்பார்க்கப்படுகின்றன.