எளிய பயன்பாடுகள் (Simple applications)

எளிய பயன்பாடுகள் (Simple applications)

இதுவரை நாம் x-ஐ தொகையீட்டு மாறியாகப் பயன்படுத்தினோம். பல நேரங்களில் தொகையிடலில் வேறுபட்ட மாறியைப் பயன்படுத்துவது அவசியமாக இருக்கும். எடுத்துகாட்டாக இயக்கச் சமன்பாட்டில் சாராமாறியாக உள்ள காலம் t ஆனது தொகையீட்டில் தொகையீட்டு மாறி t ஆக மாறும்.

கொடுக்கப்பட்ட ஒரு பொருளின் முடுக்கம் தரப்பட்டிருந்தால் அப் பொருளின் நிலை மற்றும் திசைவேகம் காண தொகையிடலை எவ்வாறு பயன்படுத்தலாம் என்பதனையும் மற்றும் இதுபோன்ற கணக்குகளையும் விவாதிக்க உள்ளோம். கணித ரீதியாகக் காணும் போது ஒரு சார்பின் வகையிடலில் தொடங்கி அதன் அசல் சார்பை காண்பதாகும். வீதம், வளர்ச்சி, தேய்மானம், இறுதிநிலை, மாற்றம், மாறுபாடுகள், உயர்த்துதல் மற்றும் குறைத்தல் போன்ற பொதுவான சொற்கள் வகையிடுதலைக் குறிக்கின்றன.

எடுத்துக்காட்டு 11.10

f'(x) = 3x2 - 4x + 5 மற்றும் f(1) = 3,எனில் f(x)-ஐக் காண்க.

தீர்வு

f'(x) = d/dx (f(x)) = 3x2 - 4x + 5 எனக் கொடுக்கப்பட்டுள்ளது.

இருபுறமும் தொகையீடு காண,

∫ f'(x)dx = ∫ (3x2-4x+5)dx 

f(x)=x3 - 2x2 + 5x + c

f(1) = 3 எனும் கொடுக்கப்பட்ட தகவலைப் பயன்படுத்தி, தொகை மாறிலி c -ன் மதிப்பைத் தீர்மானிக்கலாம்.

ƒ(1)=3⇒ 3=(1)3−2(1)2+5(1)+c⇒ c = -1 

எனவே, f(x)=x3-2x2 + 5x-1.

எடுத்துக்காட்டு 11.11

ஒரு தொடர்வண்டி மதுரை சந்திப்பிலிருந்து கோயம்புத்தூர் நோக்கி பிற்பகல் 3 மணிக்கு, v(t) = 20t + 50 கிமீ/மணி என்னும் திசை வேகத்தில் புறப்படுகிறது, இங்கு t ஆனது மணிகளில் கணக்கிடப்படுகிறது எனில், மாலை 5 மணிக்கு அத்தொடர் வண்டி எவ்வளவு தூரம் பயணித்திருக்கும்?

தீர்வு

நுண்கணிதப் பயன்பாட்டில், திசை வேகம் v = ds/dt என்பது காலத்தை பொறுத்து அதன் நிலையில் மாறும் வீதம் ஆகும். இங்கு S என்பது தொலைவினைக் குறிக்கிறது. தொடர்வண்டியின் திசைவேகம்

v(t) = 20t + 50

ஆகவே ds/dt =20t + 50

தொலைத்தூரச் சார்பு S-ஐ காண்பதற்கு வகையிடல் சார்பைத் தொகையிட வேண்டும்.

அதாவது, s = ∫ (20t + 50) dt 

                     s = 10t2 + 50t + c

காலம் பூஜ்ஜியமாக இருந்தால் தொடர்வண்டி பயணித்திருக்கும் தூரம் பூஜ்ஜியமாகும். ஆரம்ப கால நிபந்தனை t = 0 எனும் போது s = 0 எனப் பயன்படுத்தித் தொகை மாறிலி c-ஐக் கணக்கிடலாம்.

⇒ s = 10t2 + 50t + c ⇒ c = 0

எனவே, s =10t2 + 50t

2 மணி நேரத்தில் தொடர் வண்டி பயணித்த தூரம் காண t = 2 என s = 10t2 + 50t-ல் பிரதியிடவேண்டும்.

ஆகவே, s = 10(2)2 + 50(2) = 140 கிமீ. மாலை 5 மணிக்கு அத்தொடர் வண்டி 140 கி.மீ தூரம் பயணித்திருக்கும்.

எடுத்துக்காட்டு 11.12 

ஒரு நபரின் உயரம் h செ.மீ மற்றும் எடை w கி.கி. அவரின் எடையின் மாறும் வீதம் உயரத்தைப் பொறுத்துத் தோரயமாக dw / dh = 4.364 × 10-5 h2 எனக் கொடுக்கப்பட்டுள்ளது எனில், எடையை உயரத்தின் சார்பாகக் காண்க. மேலும் ஒரு நபரின் உயரம் 150 செ.மீ -ஆக இருக்கும் போது எடையைக் காண்க.

தீர்வு

உயரத்தைப் பொறுத்து எடையின் மாறுவீதம்

dw/dh = 4.364 × 10-5h2

w = ∫4.364 × 10-5h2 dh

w = 4.364 × 10-5 (h3 /3) + c

உயரம் பூஜ்ஜியம் எனும்போது அந்நபரின் எடை பூஜ்ஜயமாக இருக்கும் என்பது தெளிவு. தொடக்க நிபந்தனை h = 0 எனும்போது w = 0, என்பதை மேலே உள்ள சமன்பாட்டில் பிரதியிட்டால், தொகையீட்டு மாறிலியை c-ஐக் கணக்கிடலாம்.

w = 4.364 × 10-5 (h3 /3) + c ⇒ c = 0

ஒரு நபரின் எடை மற்றும் உயரம் ஆகியவற்றுக்கிடையேயான தொடர்பானது

w = 4.364 × 10-5 (h3 /3) ஆகும்

h = 150 செ.மீ எனில், w = 4.364 × 10-5 (1503/3)

உயரம் h = 150 செ.மீ எனும்போது, எடை தோரயமாக w = 49கி.கி ஆகும்.

எடுத்துக்காட்டு 11.13

ஒரு மரத்தின் வளர்ச்சி t ஆண்டுகளில் 18/√t செ.மீ/ஆண்டு எனும் வீதத்தில் வளர்கிறது. t = 0 என இருக்கும்போது உயரம் 5 செ.மீ இருக்கும் என எடுத்துக்கொண்டால்.

(அ) நான்கு ஆண்டிற்குப் பிறகு மரத்தின் உயரத்தைக் காண்க.

(ஆ) எத்தனை ஆண்டுகளுக்குப் பிறகு மரத்தின் உயரம் 149 செ.மீ வளர்ந்து இருக்கும்.

தீர்வு

காலம் t-ஐ பொறுத்து உயரம் h-ன் மாறு வீதம் என்பது காலம் t-ஐ பொறுத்து h-ஐ வகையீடு செய்வதாகும்.

எனவே, dh / dt = 18 / √ t = 18t- 1/2

எனவே உயரத்திற்கான பொது வடிவம் பெறுவதற்கு மேலே உள்ள சமன்பாட்டைத் தொகையிடவேண்டும்.

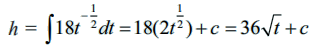
t = 0 என இருக்கும்போது உயரம் 5 செ.மீ எனக் கொடுக்கப்பட்டுள்ளது.

5 = 0 + c ⇒ c = 5 

h = 36√t+5.

(i) நான்கு ஆண்டிற்குப் பிறகு மரத்தின் உயரத்தை நாம் காண வேண்டும்.

t = 4 எனில்,

h = 36√t+5⇒ h = 36 √4+5 = 77

நான்கு ஆண்டிற்குப் பிறகு மரத்தின் உயரம் 77 செ.மீ ஆக இருக்கும்.

(ii) h = 149செ.மீ எனில், t -ஐ காண வேண்டும்.

h = 36√t + 5 ⇒ 149 = 36√t + 5

√t = 149 – 5 / 36 = 4 ⇒ t = 16

எனவே உயரம் 149 செ.மீ வளர, மரம் 16 ஆண்டுகள் எடுத்துக்கொள்கிறது.

எடுத்துக்காட்டு 11.14

மாணவன் ஒருவர் தன் மோட்டார் சைக்கிளில் 24மீ/வினாடி வேகத்தில் சென்று கொண்டிருக்கும்போது, குறிப்பிட்ட தருணத்தில் தனக்கு முன்பாக 40 மீட்டர் தொலைவில் இருக்கும்தடுப்பின் மீது மோதலைத்தவிர்க்க வாகனத்தை நிறுத்த வேண்டியுள்ளது. உடனடியாகத் தன்னுடைய வாகனத்தை 8 மீ/வினாடி2 எதிர் முடுக்கத்தில் வேகத்தைக் குறைக்கிறார் எனில் வாகனம் தடுப்பின் மீது மோதுவதற்கு முன் நிற்குமா?

தீர்வு

மோட்டார் சைக்கிளின் திசைவேகம் v எனவும் மற்றும் முடுக்கம் a எனவும் எடுத்து கொள்வோம். s என்பது தூரத்தை குறிக்கிறது. நுண்கணிதத்தில் v -ஐ v = ds / dt எனவும் a-ஐ a = dv / dt எனவும் குறிப்போம். மோட்டார் சைக்கிளின் வேகத்தைக் குறைக்கும் போது அதன் முடுக்கம் மோட்டார் சைக்கிளின் இயக்கத்தின் எதிர் திசையில் செயல்படுகிறது. ஆகையால் முடுக்கத்தைக் குறைக் குறியீடுடன் எழுதுவோம்.

மோட்டார் சைக்கிளின் எதிர்முடுக்கம் 8 மீ/வினாடி2 எனத் தரப்பட்டுள்ளது.

எனவே, a = dv/dt = -8 மீ/வினாடி2

v = ∫ adt = ∫ -8dt = −8t + c1

v = -8t+ c1.

பிரேக்கைப் பயன்படுத்தும்போது

t = 0, மற்றும் v = 24 மீ/வி.

24 = −8(0) + c1 ⇒ c1 = 24

எனவே, v = -8t + 24.

அதாவது, ds/dt = -8t + 24.

தூரம் கேட்கப்பட்டுள்ளதால் அதனைக் காண்பதற்காக மேலும் ஒருமுறை தொகையீடு காண வேண்டியது அவசியமாகிறது.

s = ∫ vdt = ∫ (-8t + 24)dt

s = -4t2 + 24t + c2

c2-ஐ தீர்மானிக்க, பிரேக்கை எங்கே உபயோகிக்கின்றோமோ, அங்கிருந்து நிறுத்தும் தூரம் s அளவிடப்படுகிறது. அதாவது, t = 0, s = 0 எனில்

s = -4t2 + 24t + c2 ⇒ 0 = - 4(0)2 + 24(0) + c2 ⇒ c2 = 0 

s = -4t2 + 24t

பிரேக்கைப் பயன்படுத்திய பின்பு மோட்டார் சைக்கிள் நிற்பதற்கான நேரம் அறிந்திருந்தால், நிறுத்துதல் தூரத்தை மதிப்பிடலாம்.திசைவேகச் சமன்பாட்டிலிருந்து நேரம் தீர்மானிக்கப்படுகிறது.

 வாகனம் நிறுத்தப்படும் போது, v = 0 ஆகும்.

⇒ v = -8t + 24 ⇒ 0 = -8t + 24 ⇒ t = 3

t = 3 எனில்

s = -4t2 + 24t ⇒ s = -4(3)2 + 24(3)

s = 36 மீட்டர் < 40 மீட்டர்

எனவே வாகனம் தடுப்பிற்கு 4 மீட்டர் முன்பே நிற்கும்.