ஆயத்தொலை வடிவியல் - அறிமுகம் | 10th Mathematics : UNIT 5 : Coordinate Geometry
10வது கணக்கு : அலகு 5 : ஆயத்தொலை வடிவியல்
அறிமுகம்
ஆயத்தொலை வடிவியல்
கோடு என்பது அகலமில்லா நீளமாகும் - யூக்ளிட்

இன்றைய துருக்கியின் பெர்காவில் பிறந்தவர் அப்போலோனியஸ் ஆவார். இவரது சிறந்த படைப்பாகக் கருதப்படும் “கூம்புகள்” மூலம் வட்டங்கள் மற்றும் பரவளையங்களை வடிவியல் ரீதியாக அறிமுகப்படுத்தினார். அவர் அடிப்படை நவீன ஆயத்தொலை வடிவியலோடு தொடர்புடைய ஆறு புத்தங்களை எழுதியுள்ளார்.
கிரகத் தேற்றத்தையும், நடைமுறைக் கணக்குகளையும் தீர்ப்பதற்கு இவரது கருத்துகள் பயன்படுத்தப்படுகின்றன. சூரியக் கடிகாரத்தை உருவாக்கித் தனது வடிவியல் திறன்களை அறிவியலின் மற்ற பிரிவுகளுக்கும் பயன்படுத்தினார். அப்போலோனியஸ் வடிவியலைப் பல துறைகளுக்குப் பயன்படுத்திய காரணத்தால் “மாபெரும் வடிவியலாளர்” எனப் போற்றப்படுகிறார்.

கற்றல் விளைவுகள்
• கொடுக்கப்பட்ட மூன்று புள்ளிகளால் உருவான முக்கோணத்தின் பரப்பைக் காணுதல்.
• கொடுக்கப்பட்ட நான்கு புள்ளிகளால் உருவான நாற்கரத்தின் பரப்பைக் காணுதல்.
• ஒரு நேர்க்கோட்டின் சாய்வைக் காணுதல்.
• பல்வேறு வகைகளில் நேர்க்கோட்டின் சமன்பாடுகளைக் கண்டறிதல்.
• ax + by + c = 0 என்ற கோட்டிற்கு இணையான நேர்க்கோட்டின் சமன்பாட்டைக் கண்டறிதல்.
• ax + by + c = 0 என்ற கோட்டிற்குச் செங்குத்தான நேர்க்கோட்டின் சமன்பாட்டைக் கண்டறிதல்.
அறிமுகம் (Introduction)
ஆயத்தொலை வடிவியல் ஆனது பகுமுறை வடிவியல் என்றும் அழைக்கப்படுகிறது. இதில் ஒரு தளத்தின் வளைவரையானது இயற்கணிதச் சமன்பாடுகள் மூலம் குறிப்பிடப்படுகின்றது. எடுத்துக்காட்டாக, x2 + y2 = 1 என்பது தளத்தில் ஓரலகு ஆரம் உடைய வட்டத்தின் சமன்பாடு ஆகும். இயற்கணிதச் சமன்பாடுகளை வடிவியல் வளைவரைகள் மூலம் குறிப்பதால் ஆயத்தொலை வடிவியல் என்பது வடிவியல் மற்றும் இயற்கணிதத்தை இணைக்கும் பாலமாகக் கருதப்படுகிறது. இந்தத் தொடர்பே வடிவியல் கணக்குகளை இயற்கணிதக் கணக்குகளாகவும், இயற்கணிதக் கணக்குகளை வடிவியல் கணக்குகளாகவும் மறு வடிவமைக்க உதவுகிறது. ஆயத்தொலை வடிவியலில் இயற்கணிதச் சமன்பாடுகளைக் காட்சி வடிவில் காண்பதால் ஆழமான புரிதல் ஏற்படுகிறது. எடுத்துக்காட்டாக, இருமாறிகளில் அமைந்த ஒருபடிச் சமன்பாடு ax + by + c = 0 ஒரு தளத்தில் நேர்க்கோட்டைக் குறிக்கும். மொத்தத்தில் கருத்துக்களைக் காட்சி வழியாகப் புரிந்துகொள்ளவும், கணிதத்தில் புதிய கிளைகளை உருவாக்கவும் ஆயத்தொலை வடிவியல் ஒரு கருவியாகிறது.
முந்தைய வகுப்புகளில் ஆயத்தொலை வடிவியலின் அடிப்படைக் கருத்துக்களான ஆயஅச்சு, ஆயதளம், புள்ளிகளைத்தளத்தில் குறித்தல், இரு புள்ளிகளுக்கு இடைப்பட்ட தொலைவு, பிரிவுச்சூத்திரம் ஆகியவை பற்றி பயின்றோம். இப்பொழுது, சில அடிப்படைச் சூத்திரங்களை நினைவு கூர்வோம்.
நினைவு கூர்தல்
இரு புள்ளிகளுக்கு இடைப்பட்ட தொலைவு
A(x1 , y1 ) மற்றும் B (x2, y2) என்ற இரு புள்ளிகளுக்கு இடைப்பட்ட தொலைவு

ஒரு கோட்டுத் துண்டின் நடுப்புள்ளி
A(x1 , y1 ) மற்றும் B (x2, y2) ஆகிய புள்ளிகளை இணைக்கும் கோட்டுத்துண்டின் நடுப்புள்ளி M ஆனது

பிரிவுச்சூத்திரம்
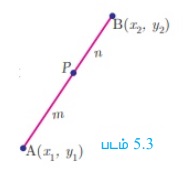
உட்புறமாகப் பிரிக்கும் புள்ளி
A(x1 , y1 ) மற்றும் B (x2, y2) ஆகிய இருவேறுபட்ட புள்ளிகளை இணைக்கும் AB என்ற கோட்டுத்துண்டை உட்புறமாக m:n என்ற விகிதத்தில் பிரிக்கும் புள்ளி P (x, y) என்பது 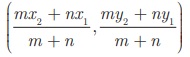 ஆகும்.
ஆகும்.
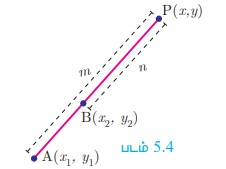
வெளிப்புறமாகப் பிரிக்கும் புள்ளி
A(x1 , y1 ) மற்றும் B (x2, y2) ஆகிய இருவேறுபட்ட புள்ளிகளை இணைக்கும் AB என்ற கோட்டுத்துண்டை வெளிப்புறமாக m:n என்ற விகிதத்தில் பிரிக்கும் புள்ளி P (x, y)
என்பது 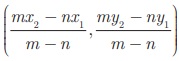 ஆகும்.
ஆகும்.
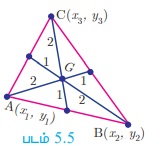
முக்கோணத்தின் நடுக்கோட்டு மையம்
A(x1 , y1 ), B (x2, y2) மற்றும் C(x 3 , y3) ஆகிய முனைகளைக் கொண்ட முக்கோணத்தின் நடுக்கோட்டு மையம் G 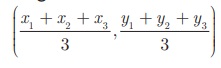 ஆகும்.
ஆகும்.
முன்னேற்றச் சோதனை
1. அட்டவணையைப் பூர்த்தி செய்க.

2. A(0, 5), B(5, 0) மற்றும் C(-4,-7) -ஐ முனைகளாகக் கொண்ட முக்கோணத்தின் நடுக்கோட்டு மையம் ----------- .