நிறைதாக்க விதி

நிறைதாக்க விதி

1864ல் நார்வே நாட்டைச் சார்ந்த மேக்மில்லன் குல்பெர்க் மற்றும் பீட்டர்வே ஆகிய வேதியியல் அறிஞர்கள் பல்வேறு மீளும் வினைகளைப் பற்றிய ஆய்வு முடிவுகளின் அடிப்படையில் நிறைதாக்க விதியினை உருவாக்கினார்கள்.

இவ்விதிப்படி,

கொடுக்கப்பட்ட ஒரு வெப்பநிலையில் எந்த ஒரு நேரத்திலும், வேதிவினையின் வேகம் என்பது அந்நேரத்தில் உள்ள வினைபடுபொருட்களின் மோலார் செறிவுகளின் பெருக்கற் பலனுக்கு நேர் விகிதத்தில் இருக்கும்.

வினைவேகம் α [வினைபடுபொருள்]x

இங்கு x என்பது வினைபடுபொருளின் வேதிவினைக் கூறு விகித குணகத்தைக் (stoichiometric co-efficient) குறிப்பிடுகிறது. சதுர அடைப்பு வினைபடு பொருளின் மோலார் செறிவினை குறிப்பிடுகிறது.

மோலார் செறிவு = (n/v) mol dm-3 (or) mol L-1

இங்கு n என்பது மோல்களின் எண்ணிக்கையையினையும், V என்பது கொள்கலனின் கனஅளவையும் (dm3 (அல்லது) L) குறிப்பிடுகின்றன.

1. சமநிலை மாறிலிகள் (Kp and Kc): 

பின்வரும் மீளும் வினையினை நாம் கருதுவோம்.

xA + yB ⇌ lC + mD

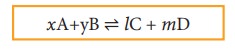
இங்கு A மற்றும் B ஆகியன வினைபடு பொருள்கள் C மற்றும் D ஆகியன வினைவிளை பொருள்கள் மேலும் x, y, l மற்றும் m ஆகியன முறையே A, B, C மற்றும் D ஆகியனவற்றின் வேதி வினைக்கூறு விகித குணகங்களைக் குறிப்பிடுகின்றன.

நிறைதாக்க விதியினைப் பயன்படுத்த, முன்னோக்கிய வினையின் வினைவேகம்,

rf α [A]x [B]y (or) rf = kf [A]x [B]y

இதைப் போலவே, பின்னோக்கிய வினையின் வினைவேகம்,

rb α [C]l [D]m

(or)

rb = kb [C]l  [D]m

இங்கு kf மற்றும் kb ஆகியன விகித மாறிலிகள் சமநிலையில்

முன்னோக்கிய வினையின் வேகம் (rf) = பின்னோக்கிய வினையின் வேகம் (rb)

kf [A]x [B]y = kb [C]1 [D]m

அல்லது

kf / kb = [C]1 [D] m / [A] x [B] y = Kc

இங்கு Kc என்பது மோலார் செறிவின் அடிப்படையிலான சமநிலை மாறிலி ஆகும். 

கொடுக்கப்பட்ட ஒரு வெப்பநிலையில், ஒரு வினையின் சமன்படுத்தப்பட்ட சமன்பாட்டில் உள்ளவாறு வினைவிளைப் பொருள்களின் மோலார் செறிவுகளின் வேதிவினைக்கூறு விகிதமடிகளின் பெருக்கற்பலனுக்கும், வினைப்படு பொருள்களின் மோலார் செறிவுகளின் வேதிவினைக்கூறு விகிதமடிகளின் பெருக்கற்பலனுக்கும் இடையேயான விகிதம் ஒரு மாறிலி ஆகும். இம்மாறிலி சமநிலை மாறிலி எனப்படுகிறது. இது தோராயமாக மட்டுமே உண்மை என வேதி வினைவேகவியல் பாடப்பகுதியை பின்னர் கற்கும்போது நாம் அறிந்து கொள்வோம்.

மேற்கண்டுள்ள வினையின், வினைபடு பொருள்கள் மற்றும் வினைவிளை பொருள்கள் ஆகியன வாயு நிலைமையில் காணப்பட்டால், சமநிலை மாறிலியை பகுதி அழுத்தங்களின் அடிப்படையில் கீழே குறிப்பிட்டுள்ளவாறு எழுத இயலும்.

Kp = Plc × Pmd / PxA × PyB

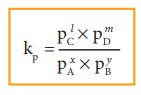
இங்கு PA,PB,PC, மற்றும் PD என்பன முறையே வாயுநிலையில் உள்ள A,B,C மற்றும் D ஆகியனவற்றின் பகுதி அழுத்தங்களாகும். 

2. Kp மற்றும் Kc ஆகியவற்றிக்கு இடையேயான தொடர்பு:

வினைபடு பொருள்கள் மற்றும் வினைவிளை பொருள்கள் ஆகிய அனைத்தும் நல்லியல்பு வாயு நிலைமையில் உள்ள பின்வரும் பொதுவான வினை ஒன்றை நாம் கருதுவோம்.

xA + yB ⇌ lC + mD

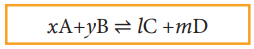
சமநிலை மாறிலி Kc ன் மதிப்பு

Kc = [C]l [D]m / [A]x [B]y   (1)

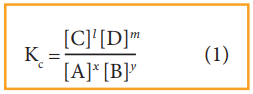
மற்றும் Kp ன் மதிப்பு

Kp = PlC × PmD / PxA × PyB  (2)

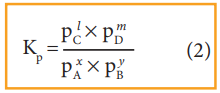
நல்லியல்பு வாயுச் சமன்பாட்டின் படி

PV = nRT 

or

P = (n / V) RT

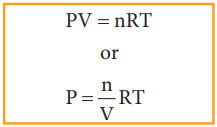
எனவே,

பகுதி அழுத்தம் (P) = மோலார் செறிவு × (RT)

மேற்கண்டுள்ளதன் அடிப்படையில் வினைபடுபொருள்கள் மற்றும் வினைவிளைப் பொருள்களின் பகுதி அழுத்தங்களை பின்வருமாறு எழுதலாம்.

PxA = [A]x (RT) x

PyB = [B]y (RT)y

PlC = [C]l (RT) l

PmD = [C]m (RT)m

சமன்பாடு (2)ல் பிரதியிட

சமன்பாடு (1) மற்றும் (4) ஐ ஒப்பிடும்போது,

Kp = Kc (RT)∆ng    (5)

இங்கு,

∆ng என்பது வாயு நிலைமையில் உள்ள வினைவிளைப்பொருள்களின் மோல்களின் மொத்த எண்ணிக்கைக்கும், வினைபடுபொருள்களின் மோல்களின் மொத்த எண்ணிக்கைக்கும் இடையேயான வேறுபாடாகும்.

எனவே, பின்வரும் தொடர்புகளை நாம் பெறலாம்.

∆ ng = 0 எனும்போது,

Kp = Kc (RT)0 = Kc

உதாரணம்:

H2(g) + I2(g) ⇌ 2HI (g)

N2 (g) + O2 (g) ⇌ 2NO (g)

∆ng ஆனது நேர்குறி மதிப்பை பெறும் போது

Kp = Kc (RT)+ve

Kp > Kc

2NH3 (g) ⇌ N2 (g) + 3H2 (g)

PCI5 (g) ⇌ PCl3 (g) + Cl2 (g) 

∆ng ஆனது எதிர்குறி மதிப்பை பெறும் போது

Kp = Kc (RT)-ve

Kp < Kc

எடுத்துக்காட்டு:

2H2 (g) + O2 (g) ⇌ 2H2O (g)

2SO2 (g) + O2 (g) ⇌ 2SO3 (g)

அட்டவணை 8.1 சில மீளும்வினைகளில், சமநிலை மாறிலிகளுக்கிடையேயானத் தொடர்பு.

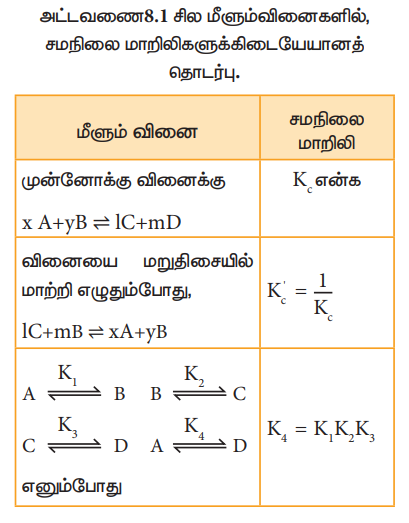
3. பலபடித்தான சமநிலைக்கான சமநிலை மாறிலி

பின்வரும் பலபடித்தான சமநிலையினைக் கருதுக.

CaCO3 (S) ⇌ CaO (S) + CO2 (g)

மேற்கண்டுள்ள வினைக்கு சமநிலை மாறிலியை பின்வருமாறு எழுத இயலும்.

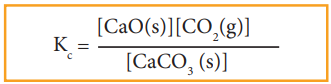
ஒரு தூய படிகமானது விரிவடைந்து கொள்கலனை அடைத்துக் கொள்ளும் தன்மையை பெற்றிருப்பதில்லை என்பதால், கொடுக்கப்பட்ட ஒரு வெப்பநிலையில், ஒரு தூய படிகம் எப்போதும் ஒரே செறிவினைக் கொண்டிருக்கும். அதாவது அதன் ஒரு லிட்டர் கனஅளவில் காணப்படும் மோல்களின் எண்ணிக்கை (மோலார் செறிவு) மாறாதிருக்கும். இதனடிப்படையில் மேற்காண் சமன்பாட்டினை பின்வருமாறு மாற்றியமைக்கலாம்.

Kc = [CO2 (g)]

 (அ)

Kp = Pco2

மேற்கண்டுள்ள வினையின் சமநிலை மாறிலியானது கார்பன்டை ஆக்ஸைடின் செறிவுனை மட்டுமே பொறுத்து அமையும். மேலும் கால்சியம் கார்பனேட் மற்றும் கால்சியம் ஆக்ஸைடு ஆகியனவற்றின் செறிவுகளைப் பொருத்து அமைவதில்லை.

இதைப்போலவே, குறிப்பிட்ட ஒரு வெப்பநிலையில், தூய திரவங்களின் மோலார் செறிவும் மாறுவதில்லை. எனவே, சமநிலை மாறிலிக்கான சமன்பாட்டினை எழுதும்போது தூய திரவங்களின் செறிவும் கணக்கில் எடுத்துக் கொள்ளப்படுவதில்லை.

எடுத்துக்காட்டு,

CO2(g) + H2O (l) ⇌ H+(aq) + HCO-3 (aq) 

இங்கு H2O (l) தூய திரவம் என்பதால் Kc ன் மதிப்பு பின்வருமாறு குறிப்பிடப்படுகிறது. 

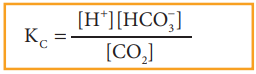
எடுத்துக்காட்டு

பின்வரும் வினைகளுக்கு Kp மற்றும் K c ஐ எழுதுக.

1) 2SO2 (g) + O 2 (g) ⇌ 2SO 3 (g)

2) 2CO(g) ⇌ CO 2 (g) + C(s)

தன்மதிப்பீடு

1. பின்வரும் வினையினைக் கருதுக.

Fe3+(aq) + SCN-(aq) ⇌ [Fe(SCN)]2+ (aq)

Fe3+ மற்றும் SCN- ஆகியன முறையே துவக்கத்தில் 1×10-3M மற்றும் 8×10-4M என்ற மோலார் செறிவுகளை பெற்றுள்ள ஒரு கரைசல் தயாரிக்கப்படுகிறது. சமநிலையில் [Fe(SCN)]2+ன் செறிவு 2×10-4M எனில், சமநிலை மாறிலியின் மதிப்பினைக் கண்டறிக.

தீர்வு :

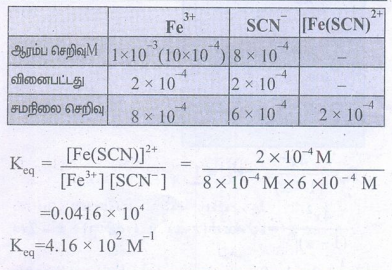
= 0.0416 × 104

K eq = 4.16 × 102 M-1

2. 1atm NO மற்றும் 1atm O2 ஐ தொடக்க செறிவுகளாகக் கொண்ட NOன் வளிமண்டல ஆக்சிஜனேற்ற வினை. 

2NO(g) + O2(g) ⇌ 2NO2 (g) 

ஆய்ந்தறியப்படுகிறது. சமநிலையில், ஆக்சிஜனின் பகுதி அழுத்தம் 0.52 atm எனில் இவ்வினைக்கான Kpன் மதிப்பைக் காண்க.

தீர்வு :

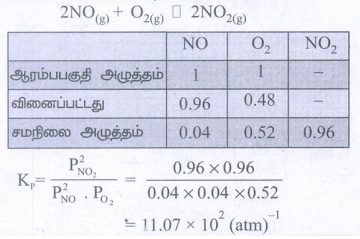
= 11.07 × 102 (atm)-1