அலைவுகள் | இயற்பியல் - பெரு வினாக்கள் | 11th Physics : UNIT 10 : Oscillations
11வது இயற்பியல் : அலகு 10 : அலைவுகள்
பெரு வினாக்கள்
அலைவுகள் (இயற்பியல்)
பெரு
வினாக்கள்
1. சீரிசை அலை இயக்கம் என்றால் என்ன? எடுத்துக்காட்டுத்தருக மற்றும் எல்லா சீரிசை இயக்கங்களும் சீரலைவு இயக்கமே ஆனால் அதன் மறுதலை உண்மையல்ல. ஏன்? விளக்குக.
• தனிச்சீரிசை இயக்கம் அலைவுறு இயக்கத்தின் சிறப்பு வகை ஆகும். துகளின் முடுக்கம் (அ) விசை நிலையான புள்ளியிலிருந்து அடைந்த இடப்பெயர்ச்சிக்கு நேர்த்தகவிலும் எப்போதும் நிலையான புள்ளியை நோக்கி இருக்கும்.
• ஒரு பரிமாண இயக்கத்தில் துகளின் இடப்பெயர்ச்சி x, முடுக்கம் ax எனில்
ax α x = ............. (1)
ax = -bx ............. (2)
b என்பது மாறிலி. இதன் பரிமாணம் T-2.
• இருபுறமும் m ஆல் பெருக்கி நியூட்டன் 2ம் விதியை பயன்படுத்த, விசை Fx = -Kx ............... (3)
K - விசை மாறிலி ஆகும். இதன் வரையறை ஓரலகு நீளத்திற்கான விசை ஆகும்.
• துகளின் இடப்பெயர்ச்சி சமநிலைப் புள்ளியிலிருந்து வலதுபுறம் (x + ve) நோக்கி உள்ளபோது விசை சமநிலை புள்ளி நோக்கி (இடதுபுறம்) இருக்கும்.
• துகளின் இடப்பெயர்ச்சி இடதுபுறம் (x - ve) நோக்கி உள்ள போது விசை சமநிலைப்புள்ளி நோக்கி (வலதுபுறம்) இருக்கும்.
• இவ்வகை விசை மீள்விசை ஆகும். ஏனெனில் தனிச்சீரிசை இயக்கத்தில் துகள் மீள்விசையால் எப்போதும் தொடக்க நிலைக்கே வரும். இது சமநிலைப் புள்ளியை நோக்கி செயல்படும் மைய கவர்ச்சி விசையாகும்.
• வெக்டர் குறியீட்டில் 
![]() என்பது ஆதிப்புள்ளியிலிருந்து துகளின் இடப் பெயர்ச்சி ஆகும்.
என்பது ஆதிப்புள்ளியிலிருந்து துகளின் இடப் பெயர்ச்சி ஆகும்.
• விசையும் இடப்பெயர்ச்சியும் நேர்ப்போக்கு தொடர்பு கொண்டது.
• செயல் (விசையின் எண்மதிப்பு ![]() ) மற்றும் விளைவு (இடப்பெயர்ச்சியின் எண்மதிப்பு
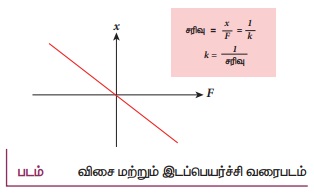
) மற்றும் விளைவு (இடப்பெயர்ச்சியின் எண்மதிப்பு ![]() ) க்கு தொடர்பை வரைபடத்தில் குறித்தால் 2ம் மற்றும் 4ம் கால்பகுதி வழியே செல்லும் நேர்கோடாக அமையும். கோட்டின் சரிவு 1/k யை அளந்து விசை மாறிலி 1/k ன் மதிப்பை கண்டறியலாம்.
) க்கு தொடர்பை வரைபடத்தில் குறித்தால் 2ம் மற்றும் 4ம் கால்பகுதி வழியே செல்லும் நேர்கோடாக அமையும். கோட்டின் சரிவு 1/k யை அளந்து விசை மாறிலி 1/k ன் மதிப்பை கண்டறியலாம்.
2. சீரான வட்ட இயக்கத்தின் வீழல் சீரிசை இயக்கம் என்பதை விவரி.
• m - நிறையுள்ள துகள் ஒன்று v சீரான திசைவேகத்தில் r ஆரம் கொண்ட வட்டத்தின் பரிதி வழியே இடஞ்சுழியாக இயங்குவதாக கருதுவோம்.
• ஆய அச்சு அமைப்பின் ஆதிப்புள்ளிவட்ட மையம் O வுடன் பொருந்துகிறது. கோண திசைவேகம் ω எனவும், t நேரத்தில் கோண இடப்பெயர்ச்சி θ எனில் θ = ω t
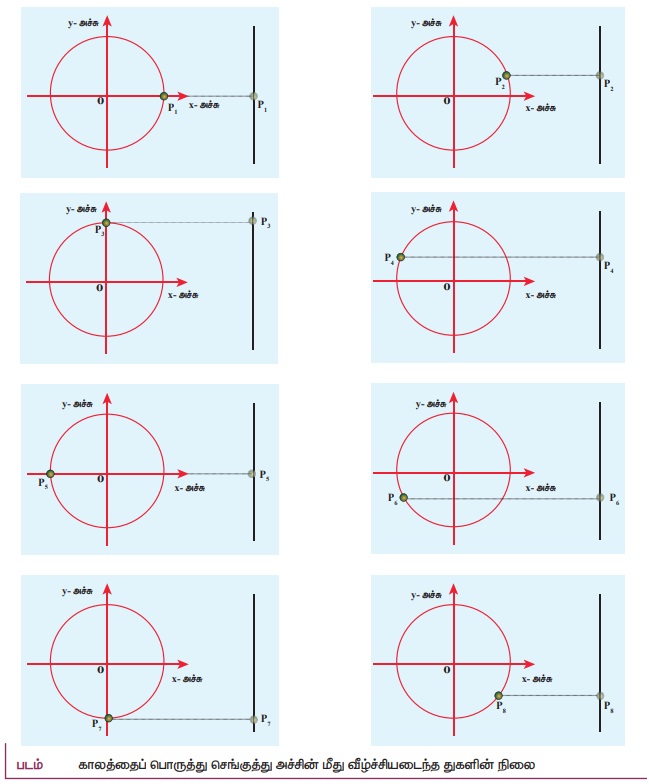
• சீரான வட்ட இயக்கத்தில் இருக்கும் ஒரு துகளின் நிலையை, அந்த வட்டத்தினுடைய விட்டத்தில் விழச்செய்தால் அந்த வீழல் ஒரு தனிச்சீரிசை இயக்கத்தை மேற்கொள்ளும்.
• இதன்மூலம் சீரான வட்ட இயக்கம் மற்றும் அதிர்வுறும் இயக்கம் ஆகியவற்றின் தொடர்பை இணைக்க முடியும். இவ்விரு இயக்கங்களும் ஒரே இயல்பைப் பெற்றுள்ளன.
• படத்தில் உள்ளவாறு வட்டப்பாதையில் இயங்கும் துகளின் நிலையை அவ்வட்டப்பாதையின் செங்குத்து விட்டத்தின் மீது அல்லது அதற்கு இணையான கோட்டின் மீது வீழல் செய்வோம்.
• ஒரு சுருள்வில் நிறை அமைப்பில் (அலைவுறும் ஊசல்) சுருள்வில் மேலும் கீழும் இயங்கும்போது (அல்லது முன்னும் பின்னும் இயங்கும் போது) அதன் நிறை அல்லது ஊசல் குண்டின் இயக்கம் வட்ட இயக்கத்தில் உள்ள புள்ளிகளுடன் இணைக்கப்பட்டுள்ளது.
• எனவே சீரான வட்ட இயக்கத்தில் துகளின் நிலையை அந்த வட்டத்தின் விட்டத்தின் மீது (அல்லது விட்டத்திற்கு இணையான கோட்டின் மீது) விழச் செய்தால் அவ்வியக்கம் நேர்க்கோட்டு இயக்கமாக அமையும். இதையே தனிச்சீரிசை இயக்கம் என்கிறோம்.
• தனிச்சீரிசை இயக்கம் ஒரு குறிப்பிட்ட வட்டத்தின் எந்த ஒரு விட்டத்தின் மீதும் இயங்கும் துகள் நிலையின் வீழ்வு எனக் கருதப்படுகிறது.
3. கோணச்சீரிசை அலையியற்றி என்றால் என்ன? அதன் அலைவுக் காலத்தை கணக்கிடுக.
• கொடுக்கப்பட்ட அச்சைப்பற்றி தனித்து சுழலும் பொருளின் அலைவுகள் கோண அலைவுகள் எனப்படும்.
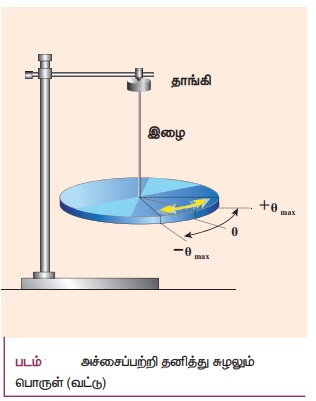
• எந்த ஒரு புள்ளியில் பொருளின் மீது செயல்படும் தொகுபயன் திருப்பு விசை சுழியாகிறதோ அப்புள்ளி சமநிலைப்புள்ளி ஆகும்.
• பொருள் சமநிலைப் புள்ளியிலிருந்து இடப்பெயர்ச்சிக்கு உள்ளாகும்போது செயல்படும் பயனுறு தொகுபயன் திருப்புவிசை கோண இடப்பெயர்ச்சிக்கு நேர்த்தகவில் இருக்கும் மற்றும் இத்திருப்புவிசை அப்பொருளை சமநிலைக்கு கொண்டு வர முயற்சிக்கும்.
• பொருளின் கோண இடப்பெயர்ச்சி ![]() தொகு பயன் திருப்புவிசை
தொகு பயன் திருப்புவிசை ![]() எனில்.
எனில்.

k = திருப்பு விசை மாறிலி.
• I பொருளின் நிலைம திருப்புத்திறன் ![]() கோண முடுக்கம் எனில்,
கோண முடுக்கம் எனில்,
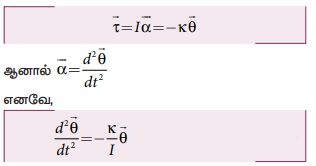
• இச்சமன்பாட்டை தனிச்சீரிசை இயக்க சமன்பாட்டோடு ஒப்பிட நாம் பெறுவது

4. சீரிசை அலை இயக்கத்திற்கும் கோண சீரிசை அலை இயக்கத்திற்கு இடையேயான வேறுபாடுகளை தருக.
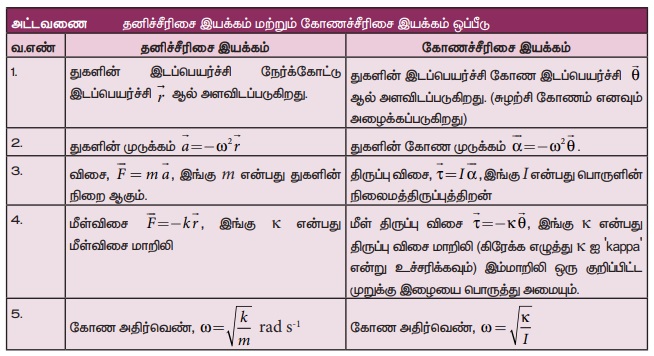
5. தனிஊசலை விரிவாக விவாதிக்க.
• தனி ஊசல் என்பது சீரலைவு இயக்கத்தை மேற்கொள்ளும் ஒரு இயந்திரவியல் அமைப்பாகும். நீளமான கயிற்றில் m நிறை கொண்ட ஊசல் குண்டு ஒரு முனையில் தொங்க விடப்பட்ட நிலையில் மறுமுனையானது தாங்கியில் பொருத்தப்பட்டுள்ளது. தனி ஊசலானது சமநிலைப் புள்ளியிலிருந்து சிறிய இடப்பெயர்ச்சிக்கு உட்படுத்தப்பட்டு விடப்படும்போது, ஊசல் குண்டானது முன்னும் பின்னும் இயக்கத்தை மேற்கொள்ளும். தனிஊசலின் நீளம் l என்பது தொங்கவிடப்பட்ட புள்ளிக்கும் ஊசல் குண்டின் ஈர்ப்பு மையத்திற்கும் இடைப்பட்ட தொலைவு ஆகும்.
• ஊசல் குண்டின் மீது எந்த ஒரு இடம் பெயர்ந்த நிலையிலும் இரு விசைகள் செயல்படுகின்றன.
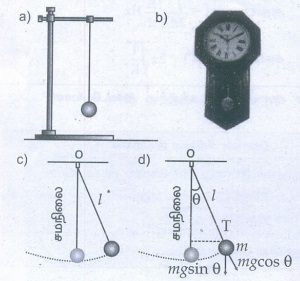
i) ஈர்ப்பியல் விசை ![]() செங்குத்தாக கீழ்நோக்கி செயல்படுகிறது.
செங்குத்தாக கீழ்நோக்கி செயல்படுகிறது.
ii) தொங்கவிடப்பட்ட புள்ளியை நோக்கி கயிற்றின் வழியாக செயல்படும் இழுவிசை T
• ஈர்ப்பியல் விசையின் இரு கூறுகளாவன:
a) செங்குத்து கூறு: கயிற்றின் வழியாக இழுவிசைக்கு எதிர்திசையில் செயல்படும் கூறு Fas = mg cos θ
b) தொடுவியல் கூறு: கயிற்றிற்கு செங்குத்தாக உள்ள கூறு அதாவது வில்லின் தொடுகோட்டு திசையில் உள்ள கூறு Fps = mg sin θ. எனவே கயிற்றின் வழியே விசையின் செங்குத்துக் கூறு
T – Was = m v2 / l
இங்கு v என்பது ஊசல் குண்டின் வேகம்
T - mg cosθ = m (v2/l) ……….(1)
• ஈர்ப்பு விசையின் தொடுகோட்டு கூறானது எப்பொழுதும் சமநிலை நோக்கியே அமையும், அதாவது ஈர்ப்பியல் விசையானது, ஊசல் குண்டின் சமநிலைப் புள்ளியிலிருந்து அடைந்த இடப்பெயர்ச்சியின் எதிர்திசையில் அமையும். இந்த தொடுவியல் விசையே மீள் விசையாகும்.
m ( d2s / dt2 ) + Fps = 0 ;
m ( d2s / dt2 ) = − Fps
m ( d2s / dt2 ) = − mg sinθ ……………(2)
• இங்கு S என்பது ஊசல் குண்டின் இடப்பெயர்ச்சியாகும். இது வட்டவில்லின் வழியே அளவிடப்படுகிறது. வட்ட வில்லின் நீளத்தை கோண இடப்பெயர்ச்சியின் வாயிலாக பெறலாம்.
s = lθ ………… (3)
• இதன் முடுக்கம் d2s / dt2 = l ( d2θ / dt2 ) ……………. (4)
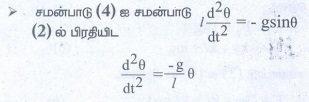
• மேற்கண்ட வகைக்கெழு சமன்பாட்டில் sin θ இருப்பதனால் இச்சமன்பாடு நேர்போக்கற்ற சமன்பாடாகும். சிறிய அலைவுகளுக்கு தோராயமாக sin θ என்பதால் மேற்கண்ட வகைக்கெழு சமன்பாடு நேர்போக்கு வகைக்கெழுச் சமன்பாடாகிறது.
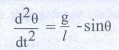
• இது நன்கு அறிந்த அலையியக்கத்திற்கான வகைக்கெழு சமன்பாடு . எனவே அலையியற்றியின் கோண அதிர்வெண் ணானது (அமைப்பில் இயல்பு அதிர்வெண்).
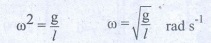
• அலையியக்கத்தின் அதிர்வெண்
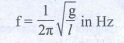
• அலையியக்கத்தின் அலைவு நேரம்
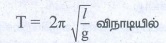
6. சுருள்வில்லின் கிடைத்தள அலைவுகளை விவரி.
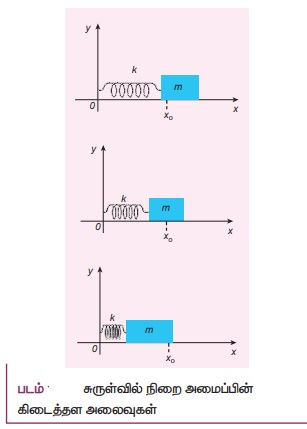
• நிறையற்ற சுருள்வில்லுடன் m நிறை கொண்ட பொருள் இணைக்கப்பட்டுள்ளது.
• இந்த சுருள்வில் நிறை அமைப்பு உராய்வற்ற கிடைத்தளத்தில் வைக்கப்பட்டுள்ளது. சுருள்வில் மாறிலி K-ஆகும்.
• விசை செயல்படாத போது m நிறையின் நடுநிலைப்புள்ளி x0 என்க. நிறையை நடுநிலைப் புள்ளியிலிருந்து x தொலைவிற்கு இடம்பெயரச் செய்து பின் விடுவித்தால் நடுநிலைப்புள்ளி x0 ஐ பொருத்து முன்னும் பின்னும் அலைவுறுகிறது.
• சுருள் வில்லின் நீட்சியால் ஏற்படும் மீள்விசை F. இவ்விசை நிறையின் இடப்பெயர்ச்சிக்கு நேர்த்தகவில் இருக்கும். F α x
F = - kx
இச்சமன்பாடு ஹீக் விதி என அழைக்கப்படுகிறது.
• நியூட்டனின் இரண்டாம் விதியிலிருந்து
m [ d2x / dt2 ] = − kx ;
d2x / dt2 = − [k/m] x ……….(1)
இச்சமன்பாட்டை தனிச்சீரிசை இயக்க சமன்பாட்டுடன் ஒப்பிட ω2 = k/m
• கோண அதிர்வெண் (அ) இயல்பு அதிர்வெண்
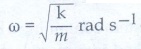 ……… (2)
……… (2)
• F அலையியற்றியின் அதிர்வெண்
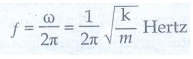 ………. (3)
………. (3)
• அலைவு நேரம்
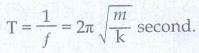 ………..(4)
………..(4)
• தனிச்சீரிசை இயக்கத்தின் வகைக்கெழுசமன்பாடு x(t) = Asin (ωt + ɸ) அல்லது x(t) - Acos (ωt + ɸ) வகைக்கெழு சமன்பாட்டின் பொதுத்தீர்வு x(t) =Asin (ωt+(ɸ)+Bcos (ωt+ ɸ) ஆகும். A,B மாறிலிகள்.
7. சுருள் வில்லின் செங்குத்து அலைவுகளை விவரி.
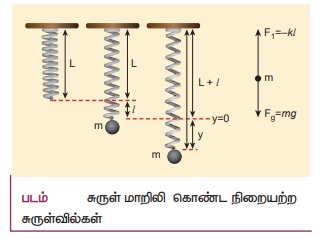
• நிறையற்ற சுருள்வில் மாறிலி k கொண்ட சுருள்வில் கூரையின் மேல்பகுதியில் இணைக்கப்பட்டுள்ளது.
• நிறை இணைக்கப்படும் முன் சுருள்வில்லின் நீளம் L என்க. மற்றொரு முனையில் நிறை m இணைக்கப்படும்போது சுருள்வில் l நீளத்திற்கு விரிவடைகிறது. நீட்சி காரணமாக ஏற்படும் மீள்விசை F1.
• நிறை m ல் செயல்படும் ஈர்ப்புவிசை செங்குத்தாக கீழ்நோக்கி செயல்படும்.
• அமைப்பு சமநிலையில் உள்ளபோது
F1 + mg = 0 …………. 1
• ஆனால் சுருள்வில் l நீட்சியடைந்துள்ளது. எனவே
F1 ∝ l ⇒ F1 = − kl ………. (2)
• சமன்பாடு (2) ஐ (1) ல் பிரதியிட
- kI + mg = 0
mg = kl
m / k = l / g ……………… 3
• மிகச்சிறிய அளவிலான புறவிசையை நிறை மீது செலுத்தினால் அந்த நிறை மேலும் கீழ்நோக்கிய திசையில் இடப்பெயர்ச்சி y-க்கு நீள்கிறது. பிறகு அது மேலும் கீழும் அலைவுறுகிறது.
• இப்போது சுருள்வில்லின் நீட்சி (y+l) காரணமாக ஏற்படும் மீள்விசை
F2 α (y+ l)
F2 = − k(y + l) = − ky – kl ….. (4)
• d2y / dt2 முடுக்கத்துடன் இயங்கும் நிறைக்கு தனித்த விசைப்படம் வரைந்தால்
− ky − kl + mg = m (d2y / dt2 ) …………..(5)
• நீட்சி காரணமாக நிறை மீது செயல்படும் மொத்த விசை
F = F2 + mg
F = − ky − kl + mg ……….. (6)
• சமன்பாடு (3) ஐ (6)ல் பிரதியிட :
F = − ky − kl + kl = − ky
• நியூட்டனின் இரண்டாம் விதியைப் பயன்படுத்த
m [d2y / dt2 ] = −ky
d2y / dt2 = [k / m] y ………….(7)

• சமன்பாடு (3) ஐ பயன்படுத்தி அலைவு நேரத்தை வேறு வடிவில் எழுதினால்
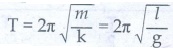
• இச்சமன்பாட்டிலிருந்து புவிஈர்ப்பு முடுக்கம் g பெறலாம்.
g = 4π2(l/ T2)ms-2
8. U வடிவக்குழாயில் திரவ தம்பத்தின் அலைவுகளைப் பற்றி சிறுகுறிப்பு வரைக.
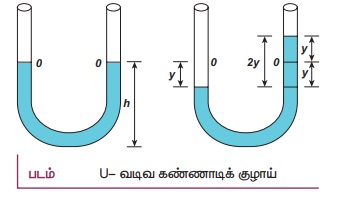
i) ஒரு சீரான குறுக்கு வெட்டுப்பரப்பு A கொண்ட திறந்த புயங்களைக் கொண்ட U வடிவக் கண்ணாடிக் குழாயை கருதுக. பாகுநிலையற்ற அமுக்க இயலாத P அடர்த்தி கொண்ட திரவமானது U வடிவக் குழாயின் புயங்களில் h உயரத்திற்கு நிரப்பப்பட்டுள்ளதாக கொள்க.
ii) குழாயும் திரவமும் அசைவற்ற நிலையில் உள்ளதெனில் திரவத்தம்ப மட்டம் சமநிலைப்புள்ளி O வில் இருக்கும்.
iii) திரவத்தின் மீது எந்த ஒரு புள்ளியில் அழுத்தத்தை அளவிட்டாலும் சமமாக இருக்கும்.
iv) மேலும் புயங்களில் மேற்பகுதியில் அழுத்தமும், குழாயின் இருபுறங்களில் உள்ள முனைகளிக் அழுத்தமும் சமம்.
v) இவ்வழுத்தம் வளிமண்டல அழுத்தத்திற்கு சமம்.
vi) அதனால் திரவமட்டங்கள் சமநிலையில் இருக்கும்.
vii) ஒரு புயத்தில் நாம் காற்றை ஊதுவதன் மூலம் தேவையான விசையை செலுத்துவதால் சமநிலைப் புள்ளி O வில் இருந்து திரவமட்டம் மாறுகிறது.
viii) ஒரு புயத்தில் ஊதப்பட்ட காற்றின் அழுத்தம் மற்றொரு புயத்தை விட அதிகம்.
ix) அழுத்த மாறுபாடு திரவத்தை நடு அல்லது சமநிலைப் பொருத்து சிறிது நேரம் அலைவுகளை உருவாக்குகிறது.
x) இறுதியாக அமைதி நிலைக்கு திரும்புகிறது. இதன் அலைவு நேரம்
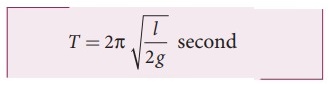
9. தனிச்சீரிசை இயக்கத்தின் ஆற்றலை விரிவாக விவாதிக்க.
தனிச்சீரிசை இயக்கத்தின் ஆற்றல் :
a) நிலை ஆற்றலுக்கான சமன்பாடு: தனிச் சீரிசை இயக்கத்தில் விசைக்கும் இடப்பெயர்ச்சிக்கும் இடையேயான தொடர்பு ஹீக் விதியின் படி
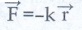
விசையை ஒரு கூறு கொண்ட ஸ்கேலார் சார்பிலிருந்து தருவிக்க முடியும்.
F = − kx ………… (1).
கீழ்க்கண்ட சமன்பாட்டிலிருந்து அதன் நிலையாற்றலைக் கணக்கிட முடியும்.
F = − dU / dx …………(2)
சமன்பாடு 1 ல் 2 ஐ ஒப்பிட - dU / dx = -kx
dU = kxdx
சிறிய இடப்பெயர்ச்சி dx ஐ மேற்கொள்ள F என்ற விசையினால் செய்யப்பட்ட வேலை நிலை ஆற்றலாக சேகரிக்கப்படுகிறது.
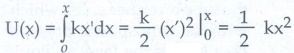 ………. (3)
………. (3)
விசை மாறிலியின் மதிப்பு k = mω2 யை சமன்பாடு 3 ல் பிரதியிட
U(x) = 1/2 mω2x2
இங்கு ω என்பது அலைவுறு அமைப்பின் இயல்பு அதிர்வெண் சீரிசை இயக்கத்தை மேற்கொள்ளும் துகள்களுக்கு நாம் பெறுவது x = A sin ωt
U(t) = 1/2 mω2A2Sin2ωt ………… (4)
b) இயக்க ஆற்றலுக்கான சமன்பாடு
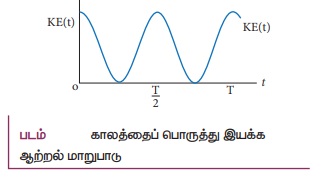
இயக்க ஆற்றல் KE = 1/2 mvx2 = 1/2 m(dx/dt)2
துகளானது சீரிசை இயக்கதை மேற்கொள்கிறது
எனில் x = A sin ωt
எனவே திசைவேகமானது.
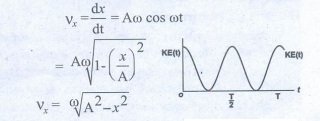
எனவே, KE = 1/2 mvx2 = 1/2 mω2 (A2 – x2 ) …….(6)
KE = 1/2 mω2A2cos2ωt ………. (7)
c. மொத்த ஆற்றலுக்கான சமன்பாடு:
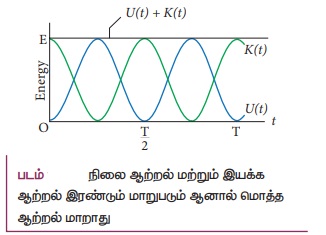
இயக்க ஆற்றல் மற்றும் நிலை ஆற்றல் இவற்றின் கூடுதல் மொத்த ஆற்றல்
E = KE + U …….. (8)
E = 1/2 mω2 (A2 – x2 ) + 1/2 mω2x2
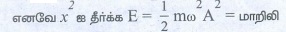 ………… (9)
………… (9)
மறுதலையாக சமன்பாடு 5 மற்றும் 6 சமன்பாடு லிருந்து நாம் பெறுவது
E = [ 1/2 m ω2 A2 Sin2ωt ] + [ 1/2 m ω2 A2 cos2ωt ]
E = 1/2 m ω2 A2 ( Sin2ωt + cos2ωt)
திரிகோண முற்றொருமையிலிருந்து
(Sin2ωt + cos2ωt) = 1
E = 1/2 m ω2 A2 = மாறிலி
எனவே மொத்த ஆற்றலைக் கொண்டு பெறப்படும் சீரிசை அலையியற்றியின் வீச்சு
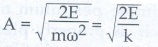
10. அலைவுகளின் நான்கு வகைகளை விரிவாக விளக்குக.
அலைவுகளின் வகைகள்
i) கட்டற்ற அலைவுகள்
அலையியற்றியை அதன் சமநிலைப்புள்ளியி லிருந்து இடம்பெயரச் செய்து அலைவுறச் செய்தால் அது அலைவுறும் அதிர்வெண்ணானது இயல்பு அதிர்வெண்ணிற்கு சமமாக இருக்கும். இவ்வகை அலைவுகள் அல்லது அதிர்வுகள் கட்டற்ற அலைவுகள் அல்லது கட்டற்ற அதிர்வுகள் எனப்படும்.
எ.கா
i) இசைக்கவையின் அதிர்வுகள்
ii) தனிஊசலின் அலைவுகள்
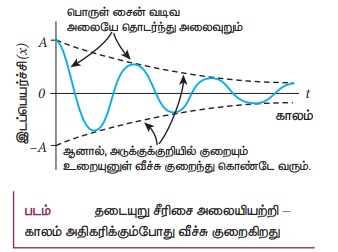
ii) தடையுறு அலைவுகள்
• தனிஊசல் அலைவுறும் போது அலைவின் வீச்சானது மாறிலி எனவும், அலையியற்றியின் மொத்த ஆற்றல் மாறாதது. ஊடகத்தின் உராய்வு மற்றும் காற்றின் இழுவையால் காலம் அதிகரிக்கும் போது வீச்சு குறைகின்றது. இதன் அலைவுகள் நிலை நிறுத்தப்படாமல் இருக்கும் மற்றும் சீரிசை அலையியற்றியின் ஆற்றல் படிப்படியாக குறைகின்றது. இந்த ஆற்றல் இழுப்பு அலையியற்றி சூழ்ந்துள்ள ஊடகம் உட்கவர்வதால் ஏற்படுகிறது. இந்த வகை அலை இயக்கம் தடையுறு அலைவுகள் என அழைக்கப்படுகின்றது.
எ.கா :
i) தொட்டிச் சுற்றில் ஏற்படும் மின்காந்த அலைவுகள்
ii) கால்வனா மீட்டரில் ஏற்படும் தடையுறு அலைவு
iii) நிறுத்தப்பட்ட அலைவுகள்:
• தடையுறு விசையின் புற மூலத்திலிருந்து ஆற்றலை பயன்படுத்தி அலையியற்றிக்கு அளிப்பதனால் அலைவுகளின் வீச்சு மாறாமல் இருக்கும். இவ்வகை அதிர்வுகளை நிலை நிறுத்தப்பட்ட அதிர்வுகள் என்கிறோம்.
எ.கா:
அதிர்வுறும் இசைக்கவையின் ஆற்றலை மின்கல அடுக்கு அல்லது புற திறன் மூலத்திலிருந்து பெறச் செய்தல்
iv) திணிப்பு அதிர்வுகள்:
திணிப்பு அதிர்வுகளில் பொருளானது ஆரம்பத்தில் இயல்பு அதிர்வெண்ணில் அதிர்வுறும் பின்னர் புற சீரலைவு விசையின் காரணமாக புற சீரலைவு விசையின் அதிர்வெண்ணில் அதிர்வுறும். இத்தகைய அதிர்வுகள் திணிப்பு அதிர்வுகள் என்று அழைக்கப்படுகிறது.
எ.கா : இழுத்துக் கட்டப்பட்ட ஒலிப்பானிலிருந்து பெறப்படும் அதிர்வுகள்