அலைவுகள் | இயற்பியல் - தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள்: நேர்போக்கு சீரிசை அலையியற்றி (LHO) | 11th Physics : UNIT 10 : Oscillations
11வது இயற்பியல் : அலகு 10 : அலைவுகள்
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள்: நேர்போக்கு சீரிசை அலையியற்றி (LHO)
எடுத்துக்காட்டு 10.8
சுருள்வில் தராசு 0.25m நீளமும் 0 முதல் 25 kg வரை நிறையை அளவிடும் வகையிலும் அமைக்கப்பட்டுள்ளது. இச்சுருள்வில் தராசானது 11.5ms-2 ஈர்ப்பு முடுக்கம் கொண்ட X என்ற நாம் அறிந்திராத கோள் ஒன்றில் எடுத்துக் கொள்ளப்படுகிறது. M kg நிறை கொண்ட ஒரு பொருள் சுருள் வில்லில் தராசில் தொங்க விடப்படும் பொழுது 0.50s அலைவுக்காலத்துடன் அலைவுறுகிறது. பொருளின் மீது செயல்படும் ஈர்ப்பியல் விசையை கணக்கிடுக.
தீர்வு
சமன்பாடு (10.29) பயன்படுத்தி, முதலில் சுருள்வில் தராசின் விறைப்பு மாறிலியை நாம் கணக்கிடலாம்.
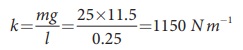
அலைவுகளின் அலைவுநேரம் 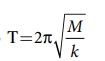
இங்கு M -ன்பது பொருளின் நிறையாகும். M என்பது தெரியாத நிறையாதலால்
சமன்பாட்டை மாற்றி அமைக்க நாம் பெறுவது
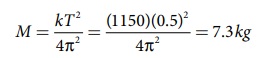
பொருளின் மீது செயல்படும் ஈர்ப்பு விசை
W = Mg = 7.3 × 11.5 = 83.95 N ≈ 84 N
சுருள்வில்களின் தொகுப்புகள்
எடுத்துக்காட்டு 10.9
1Nm-1 மற்றும் 2Nm-1 சுருள் மாறிலிகள் கொண்ட இரு சுருள்வில்கள் தொடரிணைப்பில் இணைக்கப்படுவதாக கொள்வோம். இவ்வமைப்பின் தொகுபயன் சுருள்மாறிலியைக் (ks) கணக்கிடுக. மேலும் ks, ஐ பற்றி கருத்து கூறுக.
தீர்வு
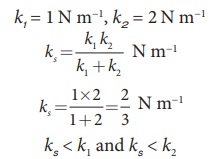
எனவே தொகுபயன் சுருள் மாறிலியானது k1 மற்றும் k2, மதிப்புகளைவிடக் குறைவாக இருக்கும்.
எடுத்துக்காட்டு 10.10
1Nm-1 மற்றும் 2Nm-1 சுருள் மாறிலி கொண்ட இரு சுருள்வில்கள் பக்க இணைப்பில் இணைக்கப்படுவதாகக் கொள்வோம். தொகுபயன் சுருள்மாறிலியைக் கணக்கிடுக மேலும் kp ஐ பற்றி கருத்து கூறுக.
தீர்வு
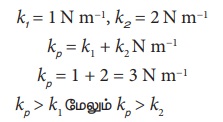
எனவே தொகுபயன் சுருள்மாறிலியானது k1. மற்றும் k2 மதிப்பைவிட அதிக மதிப்பு கொண்டது.
எடுத்துக்காட்டு 10.11
கீழ்க்காணும் அமைப்புகளின் தொகுப்பயன் சுருள்வில் மாறிலியின் மதிப்பைக் கணக்கிடுக. அனைத்து சுருள்வில்களுக்கும் சுருள்மாறிலிகளின் மதிப்பு சமம் எனக் கொண்டு கணக்கீடு செய்க.
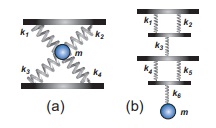
தீர்வு
a. k1, மற்றும் k2, பக்க இணைப்பில் உள்ளதால், ku = k1 + k2
இதேபோல், k3, மற்றும் k4, பக்க இணைப்பில் kd = k3 + k4
ku, மற்றும் kp, ஆகியவை தொடரிணைப்பில் உள்ளன.
எனவே 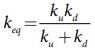
அனைத்து சுருள்வில் மாறிலிகளும் சமம் என்பதால்
k1 = k2 = k3 = k4 = k
அதாவது ku = 2k மற்றும் kd = 2k
எனவே, 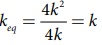
b. k1, மற்றும் k2, பக்க இணைப்பில் உள்ளதால்,
kA = k1 + k2
இதேபோல், k4, மற்றும் k5 உள்ளதால்,
kB = k4 + k5
kA, k3, kB, மற்றும் k6, தொடரிணைப்பில்
உள்ளதால் 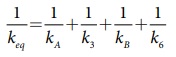
அனைத்து சுருள் மாறிலிகளும் சமம் என்பதால் k1 = k2 = k3 = k4 = k5 = k6 = k எனவே kA = 2k மற்றும் kB = 2k
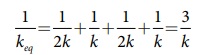
keq = k/3
எடுத்துக்காட்டு 10.12
m நிறையானது v என்ற வேகத்தில் ஒரு உராய்வற்ற கிடைத்தள பரப்பில் சென்று, ஏறத்தாழ நிறையற்ற, சுருள் மாறிலி k கொண்ட சுருள்வில் மீது மோதுகின்றது. மோதலுக்கு பிறகு நிறையானது அமைதி நிலைக்கு வருகின்றது எனில் சுருள்வில்லின் அமுக்கத்தை கணக்கிடுக.
தீர்வு
நிறையானது சுருள்வில்லை மோதும்போது நிறையின் இயக்க ஆற்றல் இழப்பானது சுருள்வில்லில் மீள் நிலை ஆற்றலாக பெறப்படுகிறது. (ஆற்றல் மாறாக்கோட்பாட்டின்படி)
x என்பது சுருளின் இறுக்கமடைந்த தூரம் என்க, ஆற்றல் மாறாக் கோட்பாட்டின்படி
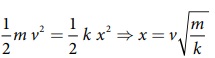
தனிச்சீரிசை இயக்கத்தில் தனி ஊசலின் அலைவுகள் மற்றும் தனிஊசலின் விதிகள்
எடுத்துக்காட்டு 10.13
தனி ஊசல் சோதனைகளில், தோராயமாக சிறிய கோணங்களை பயன்படுத்துவோம். இச்சிறிய கோணங்களை விவாதிக்க
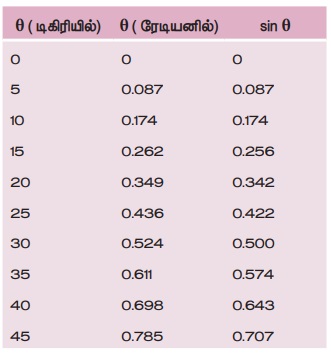
θ என்பது ரேடியனில் உள்ளபோது, சிறிய கோணங்களுக்கு sin θ ≈ θ
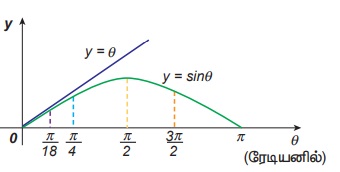
அதாவது θ வானது 10 டிகிரி மற்றும் அதைவிட குறைவாக இருக்கும்போது, θ வை ரேடியனில் குறிப்பிட்டால் sin θ வானது θ வுக்கு சமம். θ அதிகரிக்கும் பொழுது sine θ மதிப்பானது θ விலிருந்து படிப்படியாக வேறுபடுகிறது.
எடுத்துக்காட்டு 10.14:
ஒரு தனி ஊசலின் நீளம் அதன் தொடக்க நீளத்திலிருந்து 44% அதிகரிக்கிறது எனில் தனி ஊசலின் அலைவுநேரம் அதிகரிக்கும் சதவீதத்தை கணக்கிடுக.
தீர்வு
