கிடைத்தளத்தில் எறியப்படும் எறிபொருளின் இயக்கம்

கிடைத்தளத்தில் எறியப்படும் எறிபொருளின் இயக்கம் 

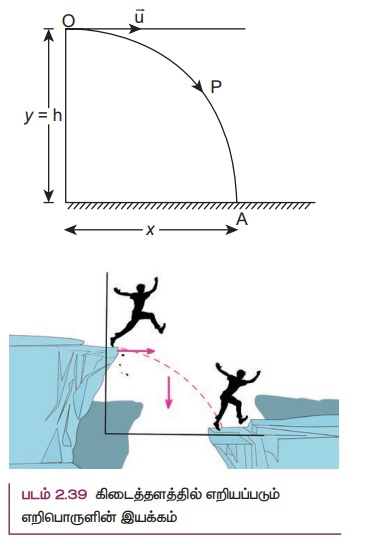
எறிபொருள் ஒன்றைக் கருதுக, அதாவது h உயரமுள்ள கட்டிடம் ஒன்றின் உச்சியிலிருந்து (படம் 2.39) என்ற தொடக்கத் திசைவேகத்துடன் கிடைத்தளத்தில் எறியப்படும் பந்து ஒன்றினைக் கருதுக .

பந்து இயங்கும் போது என்ற மாறாத கிடைத்தள திசைவேகத்தினால் கடக்கும் கிடைத்தளத் தொலைவையும் சீரான புவியீர்ப்பு முடுக்கத்தினால் கடக்கும் கீழ்நோக்கிய செங்குத்துத் தொலைவையும் பெற்றிருக்கும். எனவே, இவ்விரண்டு விளைவுகளினால் பந்து OPA என்ற பாதையில் இயங்கும். இவ்வியக்கம் இருபரிமாணத் தளத்தில் உள்ளது. பந்து தரையில் உள்ள A புள்ளியை அடைய எடுத்துக் கொள்ளும் நேரம் t என்க. 

பந்து கடந்த கிடைத்தளத் தொலைவு, x (t) = x

பந்து கடந்த செங்குத்துத் தொலைவு, y (t) = y

நாம் இயக்கச் சமன்பாடுகளை தனித்தனியே x அச்சுத் திசையிலும் மற்றும் y அச்சுத் திசையிலும் பயன்படுத்த வேண்டும். இங்கு எறிபொருளின் இயக்கம் இருபரிமாணமுடையது. எனவே திசைவேகம், கிடைத்தளக் கூறு ux மற்றும் செங்குத்துக் கூறு uy, ஆகிய இரு கூறுகளையும் பெற்றிருக்கும்.

கிடைத்தளத்திசையில் எறிபொருளின் இயக்கம் 

பந்து ‘x’ அச்சுத்திசையில் எவ்வித முடுக்கத்தினையும் பெற்றிருக்கவில்லை. எனவே இயக்கம் முழுவதும் தொடக்கத் திசைவேகம் மாறாத மதிப்பைப் பெற்றிருக்கும்.

‘t’ நேரத்தில் எறிபொருள் கடந்த கிடைத்தளத் தொலைவு x = uxt + 1/2 at2.

இங்கு x இன் திசையில் a = 0, எனவே

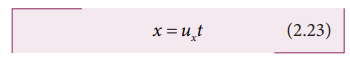
கீழ்நோக்கியத்திசையில் எறிபொருளின் இயக்கம்

இங்கு uy, = 0 (ஆரம்பத் திசைவேகத்திற்கு கீழ் நோக்கியக் கூறு இல்லை) a = g (கீழ்நோக்கிய இயக்கத்தை நேர்க்குறி y அச்சு வழியே குறிப்பிடவும்), மேலும் s = y

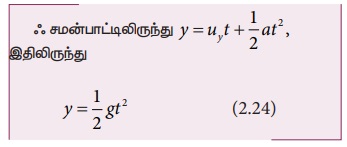
சமன்பாடு (2.23) லிருந்து ‘t’ இன் மதிப்பை சமன்பாடு (2.24) இல் பிரதியிட்டால்

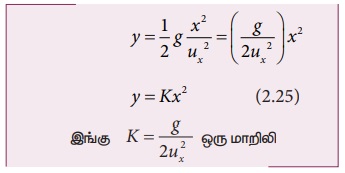
சமன்பாடு (2.25) ஒரு பரவளையச் சமன்பாடு எனவே எறிபொருளின் பாதை ஒரு பரவளையம் ஆகும். 

(1) பறக்கும் நேரம் : எறிபொருள் தன்னுடைய பாதையை நிறைவு செய்ய எடுத்துக் கொள்ளும் நேரம் அல்லது எறிபொருள் எறியப்பட்ட கணத்திலிருந்து, தரையை அடைய எடுத்துக்கொள்ளும் நேரம் பறக்கும் நேரம் எனப்படும்.

எடுத்துக்காட்டாக, கட்டிடத்தின் உயரம் h என்க. எறிபொருள் எறியப்பட்ட கணத்திலிருந்து அதன் பாதை வழியே தரையை அடைய எடுத்துக்கொண்ட நேரத்தை T என்க.

நாம் அறிந்தபடி செங்குத்து இயக்கத்திற்கு

sy = uyt + 1/2 at2

இங்கு sy = h, t = T, uy = 0 (ஆரம்ப செங்குத்துத் திசைவேகம் சுழி)

a = g (எறிபொருள் புவி ஈர்ப்பு விசையின் காரணமாக கீழே விழுகிறது)

எனவே, பறக்கும் நேரம் கட்டிடத்தின் உயரத்தைச் சார்ந்துள்ளது, ஆனால் அது கிடைத்தளத் திசைவேகத்தைச் சார்ந்ததல்ல. ஒரு பந்து செங்குத்தாக மேலிருந்து கீழ் நோக்கி விழுகிறது, அதே நேரத்தில் ஒரு குறிப்பிட்ட திசைவேகத்தில் பந்து ஒன்று கிடைத்தளத்தில் வீசி எறியப்படுகிறது. இவ்விரண்டு பந்துகளும் ஒரே நேரத்தில் தரையை அடையும். இது படம் 2.40 இல் சுட்டிக்காட்டப்பட்டுள்ளது.

(2) கிடைத்தள நெடுக்கம்: எறியப்பட்ட புள்ளிக்கு நேர் கீழே கட்டிடத்தின் தரையிலிருந்து எறிபொருள் தரையை அடைந்த புள்ளி வரை உள்ள தொலைவு, கிடைத்தள நெடுக்கம் எனப்படும். 

நாம் அறிந்தபடி கிடைத்தள இயக்கத்தில்

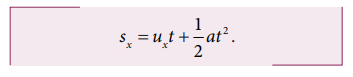
இங்கு, sx = R (கிடைத்தள நெடுக்கம்), ux = u, a = 0 (கிடைத்தளத்திசையில் முடுக்கம் இல்லை), பறக்கும் நேரம் 'T', எனவே கிடைத்தள நெடுக்கம் = uT.

நாம் அறிந்தபடி பறக்கும் நேரம் =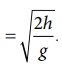

எனவே கிடைத்தள நெடுக்கம்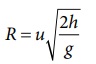

மேற்கண்ட சமன்பாட்டிலிருந்து கிடைத்தள நெடுக்கம் ஆரம்பத் திசை வேகத்திற்கு (u) நேர்த்தகவிலும், புவியீர்ப்பு முடுக்கத்தின் (g) இருமடி மூலத்திற்கு எதிர்த்தகவிலும் உள்ளதைக் காட்டுகிறது. 

(3) தொகுபயன் திசைவேகம் (ஒரு குறிப்பிட்ட நேரத்தில் எறிபொருளின் திசைவேகம்) 

ஒரு குறிப்பிட்ட நேரம் t யிலும் எறிபொருளுக்கு x - அச்சு மற்றும் y-அச்சு ஆகிய இரண்டு அச்சுகளிலும் திசைவேகக் கூறுகள் உள்ளன. இவ்விரண்டு கூறுகளின் தொகுபயன், எறிபொருளின் தொகுபயன் திசைவேகத்தைக் கொடுக்கும்.

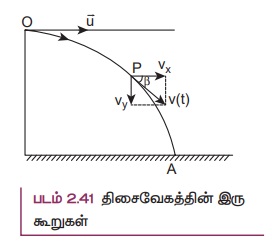
படம் 2.41 லிருந்து கீழ்க்கண்டவாறு சமன்பாடுகளை எழுதலாம்.

கிடைத்தளத்திசையில் (x-அச்சில்) திசைவேகக்கூறு vx = ux + axt

இங்கு, ux = u, ax = 0 எனவே

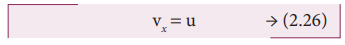
செங்குத்துத்திசையில் (y அச்சில்) திசைவேகக்கூறு vy = uy + ayt 

இங்கு, uy = 0, ay = g எனவே

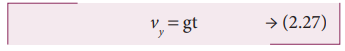
எந்தவொரு குறிப்பிட்ட நேரத்திலும் எறி பொருளின் திசைவேகம்

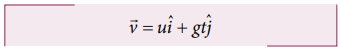
எந்தவொரு குறிப்பிட்ட நேரத்திலும் எறிபொருளின் வேகம்

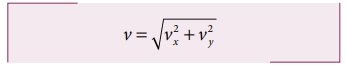
எறிபொருள் தரையைத் தொடும்போது அதன் வேகம்

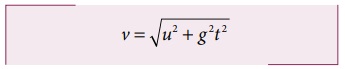
எறிபொருள் எறியப்பட்ட கணத்திலிருந்து, தரையை அடைய எடுத்துக் கொள்ளும் நேரம்

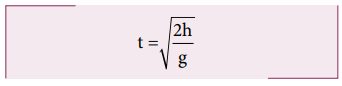
எறிபொருளின் கிடைத்தளத்திசைவேகக்கூறு மாறாதது அதாவது

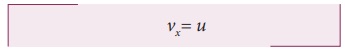
T நேரத்தில் எறிபொருளின் செங்குத்துத் திசைவேகக்கூறு

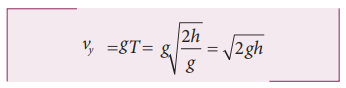
எனவே எறிபொருள் தரையைத் தொடும் போது அதன் வேகம்

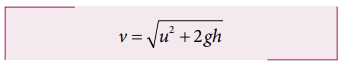
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் எறிபொருளின் இயக்கம்

எடுத்துக்காட்டு 2.37

எறிபொருள் ஒன்று 10 m s-1 என்ற ஆரம்பத் திசைவேகத்துடன், கிடைத்தளத்துடன் π/4 கோண அளவில் எறியப்படுகிறது. அதன் கிடைத்தளத் நெடுக்கத்தைக் கண்டுபிடி, அதே எறிபொருளை முன்னர் எறிந்தவாறே நிலவில் எறியும் போது அதன் கிடைத்தள நெடுக்கத்தில் ஏதேனும் மாற்றம் நிகழுமா? நிகழும் எனில் எவ்வகையான மாற்றம் என்று விளக்குக.

(நிலவின் ஈர்ப்பு முடுக்கம் gநிலவு = 1/6 g)

தீர்வு 

எறிபொருள் இயக்கத்தில் கிடைத்தள நெடுக்கம்

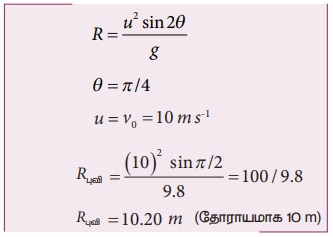
இதே எறிபொருளை நிலவில் எறியும் போது அதன் கிடைத்தள நெடுக்கம் அதிகரிக்கும் ஏனெனில் நிலவின் ஈர்ப்பு முடுக்கம், புவியின் ஈர்ப்பு முடுக்கத்தைவிடக் குறைவு.

நிலவில் எறிபொருளின் கிடைத்தள நெடுக்கம், புவியில் எறிபொருளின் கிடைத்தள நெடுக்கத்தை விட ஆறுமடங்கு அதிகம்.

எடுத்துக்காட்டு 2.38

படத்தில் காட்டியவாறு கிரிக்கெட் வீரர் பந்து ஒன்றினை மட்டையால் அடித்த பின்பு, அப்பந்து 30 m s-1 என்ற திசைவேகத்துடனும், 30° கோணத்திலும் பறந்து செல்கிறது. மைதானத்தின் எல்லையானது பந்தினை அடித்த கிரிக்கெட் வீரரிலிருந்து 75 m தொலைவில் உள்ளது. அப்பந்து மைதானத்தின் எல்லையை பறந்து சென்று கிரிக்கெட் வீரருக்கு ஆறு ரன்களைப் பெற்றுத்தருமா? (காற்றுத்தடையைப் புறக்கணிக்கவும் மற்றும் புவியீர்ப்பு முடுக்கம் g = 10 m s-2 எனக் கருதுக).

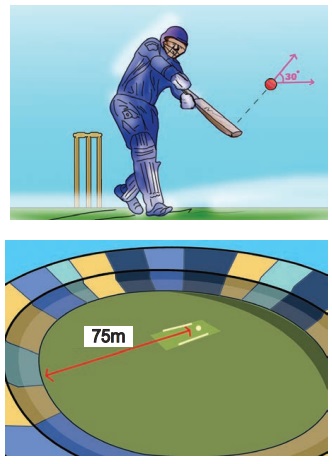
தீர்வு 

கிரிக்கெட் பந்தின் இயக்கத்தை எறிபொருளின் இயக்கமாகக் கருதலாம். நாம் முன்னர் பார்த்தபடி கிடைத்தளத் தொலைவு

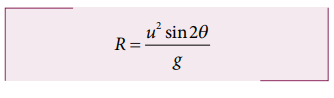
ஆரம்பத்திசை வேகம் u = 30ms-1

எறிகோணம் θ = 30°

கிரிக்கெட் பந்தின் கிடைத்தள நெடுக்கம்

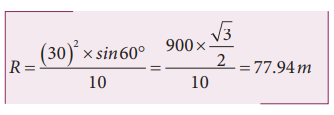
கிடைத்தள நெடுக்கம் மைதானத்தின் எல்லையான 75 மீட்டரை விட அதிகமாக உள்ளது. எனவே, பந்து எல்லையைக் கடந்து பறந்து வீரருக்கு ஆறு ரன்களைப் பெற்றுத் தரும்.