பண அளவு கோட்பாடுகள்

பண அளவு கோட்பாடுகள்

பண அளவுக் கோட்பாடுகள் பணத்தின் அளவிற்கும், பணத்தின் மதிப்பிற்கும் இடையேயான தொடர் பினை எடுத்துரைப்பதாகும். இங்கு, பிஷரின் பண அளவுக் கோட்பாடு மற்றும் கேம்பிரிட்ஜ் ரொக்க இருப்பு அணுகுமுறை கோட்பாடு ஆகியன கொடுக்கப்பட்டுள்ளன.

அ) ஃபிஷரின் பண அளவுக் கோட்பாடு

பண அளவுக் கோட்பாடு என்பது மிக பழமையான கோட்பாடு ஆகும். இது 1588ஆம் ஆண்டு டாவன்ஷட்டி என்ற இத்தாலிய பொருளியல் அறிஞரால் முன்மொழியப்பட்டது. ஆனால், நவீன வடிவிலான இக்கோட்பாட்டினை உருவாக்கிய புகழ் முழுதும் "பணத்தின் வாங்கும் சக்தி" (1911) என்ற நூலை எழுதிய அமெரிக்க பொருளியலறிஞரான இர்விங் ஃபிஷரைச் சாரும். இவர் தனது கோட்பாட்டினை "பரிவர்த்தனைக்கான சமன்பாடு" என்று கணித சமன்பாட்டின் வாயிலாக வழங்கியுள்ளார்.

இச்சமன்பாட்டின் பொது வடிவம் ஆகும்.

இங்கு,

( MV = PT )

M = மொத்த (காகித) பண அளவு 

V = பணத்தின் சுழற்சி வேகம்; 

P = பொது விலை மட்டம் 

T = வாணிபத்தின் அளவு

ஃபிஷர் ஒரு நாட்டில் குறிப்பிட்ட கால அளவில் மொத்த பண அளிப்பு (MV) என்பது நாட்டில் வாங்க-விற்கப்படும் பொருட்கள் மற்றும் பணிகளின் அளவின் பண மதிப்பிற்கு (அதாவது மொத்த பணத்தேவைக்கு) (PT) சமமாக இருக்கும் என்று குறிப்பிடுகின்றார்.

MV = PT 

பண அளிப்பு = பணத்தேவை

இச் சமன்பாடு "ரொக்க பரிவர்த்தனை சமன்பாடு" என்றும் அழைக்கப்படுகிறது.

மேற்சொன்ன சமன்பாட்டினை P = MV/T என்று மாற்றியமைக்கும்பொழுது, பண சுழற்சி வேகமும், வாணிபத்தின் அளவும் மாறாதிருக்கும் சூழ்நிலையில் பணத்தின் அளவு எவ்வகையில் பொது விலைமட்டத்தையும், பணத்தின் மதிப்பினையும் நிர்ணயிக்கிறது என்பதை விளங்குகின்றது. இங்கு பண அளவு மாறுதல் நேரடியாக விலைமட்டத்தை பாதிக்கிறது.

மேற்சொன்ன சமன்பாடு காகிதப் பணத்தை மட்டுமே கணக்கில் கொண்டுள்ளது. ஆனால், நவீன வாணிப பொருளாதாரத்தில் காகிதப் பணத்துடன் வங்கியிலிருக்கும் கேட்பு வைப்புக்கள், கடன் பணம் மற்றும் அவைகளின் சுழற்சி வேகம் ஆகிய அனைத்தும் முக்கிய பங்கு வகிக்கின்றன. ஆகவே, ஃபிஷர் தனது சமன்பாட்டினை கீழ்கண்டவாறு விரிவாக்கினார்:

PT = MV + M1V1

P = MV + M1V1 / T

மேற்கண்ட விரிவாக்கப்பட்ட சமன்பாட்டில், பொது விலைமட்டமானது (P) காகிதப் பண அளவு (M) , பணத்தின் சுழற்ச்சி வேகம் (V), வங்கி கடன் பணத்தின் அளவு (M1) வங்கிக் கடன் பணத்தின் சுழற்ச்சி வேகம் (V1) மற்றும் மொத்த வாணிபத்தின் அளவு (T) ஆகிய காரணிகளால் நிர்ணயிக்கப்படுகிறது.

வரைபட விளக்கம்

வரைபடம் (A) மொத்த பண அளவில் ஏற்படுத்தப்படும் மாறுதல் விலைமட்டத்தில் எவ்வாறு மாற்றத்தினை ஏற்படுத்துகிறது என்பதனை உணர்த்துகிறது. பண அளவு OM ஆக இருக்கும்பொழுது விலைமட்டம் OPயாக உள்ளது. பிறகு பண அளவினை OM2 என இரட்டிப்பாக்கும் பொழுது விலைமட்டமும் OP2 என இரட்டிப்பாகிறது. மேலும், பண அளவு OM4 என நான்கு மடங்காக்கும் பொழுது விலைமட்டமும் OP4 என நான்கு மடங்காகிறது. விலைமட்டச் சார்பு OP = f(M) க்கான நேர்கோடு வரைபடத்தின் தோற்றுவாயிலிருந்து 45° அமையும்பொழுது பணத்தின் அளவிற்கும் விலைமட்டத்திற்கும் உள்ள நேரடி சமவிகித உறவு விளங்குகிறது.

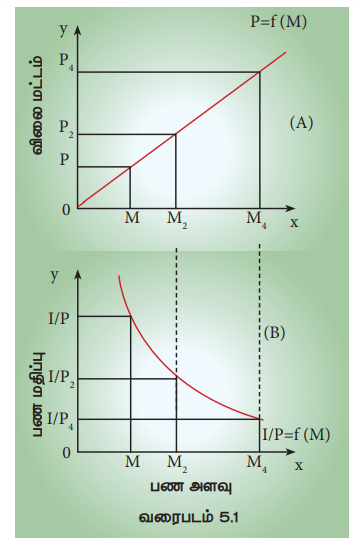
வரைபடம் (B) பணத்தின் அளவிற்கும், பணத்தின் மதிப்பிற்கும் உள்ள தலைகீழ் உறவினை விளக்குகிறது. வரைபடத்தின் செங்குத்து அச்சில் பண மதிப்பும் (O1/P) படுகிடை அச்சில் பண அளவும் (M) குறிக்கப்பட்டுள்ளன. பண அளவு OM ஆக உள்ளபொழுது, பணமதிப்பு O1/P -ஆக உள்ளது. பின்னர் பண அளவினை OM2 என இரட்டிப்பாக்கும் பொழுது பண மதிப்பு O1/P2 என பாதியாக குறைகிறது. தொடர்ந்து பண அளவினை OM4 என நான்கு மடங்காக்கும்பொழுது பணமதிப்பு O1/P4 என நான்கில் ஒரு பகுதியாக குறைகிறது. பண மதிப்புச் சார்பு O1/P = f(M) க்கான வளைகோடு மேலிருந்து கீழ்நோக்கி சார்ந்து பண அளவிற்கும் பண மதிப்பிற்கும் உள்ள எதிர்மறையான மற்றும் சமவிகித தொடர்பினை சுட்டிக்காட்டுகிறது.

ஆ) கேம்பிரிட்ஜ் அணுகுமுறை (ரொக்க இருப்பு அணுகுமுறை)

i) மார்ஷலின் சமன்பாடு

மார்ஷலின் சமன்பாடு பின்வருமாறு வழங்கப்பட்டுள்ளது:

M = KPY

இங்கு ,

M = பணத்தின் அளவு 

Y = சமுதாயத்தின் மொத்த உண்மை வருமானம் 

P = பொது விலைமட்டம் 

K = மக்கள் தங்கள் கையில் ரொக்கமாக வைத்திருக்க விரும்பும் சமுதாயத்தின் மொத்த உண்மை வருமானத்தின் ஒரு பகுதி

மேற்கண்ட சமன்பாட்டினை மாற்றி எழுதும் பொழுது, P=M/KY என்று பொதுவிலை மட்டத்தினை (P) காண உதவுகிறது. மேலும் அதனை தலைகீழியாக மாற்றி எழுதும் பொழுது நமக்கு 1/P=KY/M என பணத்தின் வாங்கும் சக்தி, அதாவது பண மதிப்பினை கண்டறிய முடிகிறது.

இறுதியாக கூறப்பட்ட 1/P=KY/M என்ற சமன்பாட்டினை மேலும் சற்று விளக்கமாக கூற வேண்டுமெனில், மக்கள் தங்கள் கையில் வைத்திருக்க விரும்பும் உண்மை வருமானத்தை (KY = மொத்த பணத்தேவையின் அளவு) பண அளிப்பினால் (M) வகுத்தால் பணத்தின் மதிப்பினை கண்டறியலாம்.

மார்ஷல் கூற்றுப்படி, பண அளவு (M) என்ற காரணியைவிட மக்கள் தங்கள் கையில் ரொக்கமாக வைத்திருக்க விரும்பும் உண்மை வருமானத்தின் பகுதி (K என்ற கெழு) பணமதிப்பினை தீர்மானிப்பதில் மிக முக்கிய பங்கினை வகிக்கறது.

ii) கீன்ஸின் சமன்பாடு

கீன்ஸின் முதல் சமன்பாடு பின்வரும் வகையில் அமைகின்றது:

n = pk (or) p = n / k

இங்கு, 

N = மொத்த பண அளிப்பு 

p = நுகர்ச்சிப் பொருட்களின் விலை மட்டம்

k = மக்கள் தங்கள் கையில் வைத்திருக்க விரும்பும் வருமானத்தின் ஒரு பகுதி - நுகர்ச்சிப் பொருட்களின் அலகுகளில்

கீன்ஸ் k என்பதனை உண்மை இருப்பு (Real Balance) என்று குறிப்பிடுகிறாh; ஏனெனில் மக்களின் ரொக்க கையிருப்பு இங்கு நுகர்ச்சிப் பொருட்களின் அளவுகளில் கணக்கிடப்படுகிறது.

கீன்ஸின் கூற்றுப்படி, மக்களின் ரொக்க விருப்பத்தினை (k) பணவியல் அமைப்புகள் மாற்று இயலாது, ஆகவே, பணத்தின் அளவை (n) நெறிப்படுத்துவதன் மூலம் விலைவாசியை கட்டுப்படுத்தலாம், பணத்தின் மதிப்பினை நிலைப்படுத்தலாம் என்கிறார்.

பின்னர், கீன்ஸ் தனது சமன்பாட்டினை பின்வருமாறு விரிவாக்குகிறார்:

n = p (k+ rk1) my1yJ p=n/(k + rk1)

n = மொத்த பண அளிப்பு

p = நுகர்ச்சிப் பொருட்கள் (தொகுப்பின்) விலை மட்டம்

k = மக்கள் தங்கள் கையில் வைத்திருக்க விரும்பும் வருமானத்தின் ஒரு பகுதி - நுகர்ச்சிப் பொருட்களின் எண்ணிக்கையில் (பல பொருட்களின் தொகுப்பு).

r = வங்கிகளின் ரொக்க இருப்பு விகிதம்

k' = வங்கி வைப்புகளாக சமுதாயம் வைத்திருக்கும் பணத்தின் அளவு – நுகர்ச்சிப் பொருட்களின் எண்ணிக்கையில்.

இவ்விரிவாக்கச் சமன்பாட்டிலும், கீன்ஸ் k, k' மற்றும் r ஆகியவைகள் மாறாதிருக்கும் என்கிறார். அச்சூழ்நிலையில், பண அளவை (n) மாற்றும் பொழுது விலைமட்டம் (P) நேரடியாகவும், சமவிகிதத்திலும் மாறும் என்கிறார்.