நேர்க்கோடு

நேர்க்கோடு (Straight line)

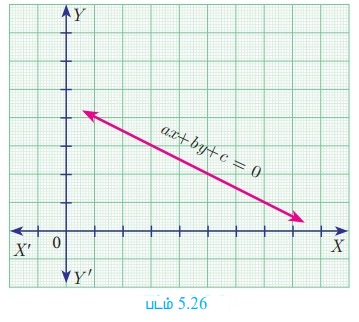
x, y எனும் இரு மாறிலிகளில் அமைந்த ஒருபடிச் சமன்பாடு ax + by +c = 0 …(1) என்பது xy  தளத்தில் அமைந்த ஒரு நேர்க்கோடாகும். இங்கு, a, b, c ஆகியன மெய்யெண்கள் மற்றும் a, b -யில் ஏதேனும் ஒன்றாவது பூச்சியமற்றதாகும்.

1. ஆய அச்சுகளின் சமன்பாடு (Equation of coordinate axes)

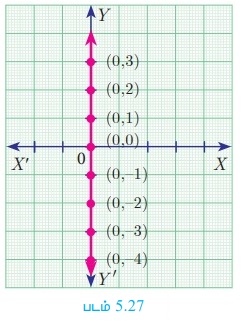
X மற்றும் Y அச்சுகளை ஆய அச்சுகள் என அழைக்கிறோம். OY-ன் (Y அச்சு) மீதுள்ள x -ஆயப் புள்ளியின் ஒவ்வொரு புள்ளியும் பூச்சியம் ஆகும். எனவே, OY (Y அச்சு)-ன் சமன்பாடு x = 0 (படம் 5.27)

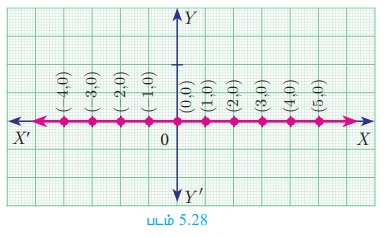
OX -ன் (X அச்சு) மீதுள்ள y -ஆயப் புள்ளியின் ஒவ்வொரு புள்ளியும் பூச்சியம் ஆகும். எனவே, OX (X அச்சு)-ன் சமன்பாடு y = 0 (படம் 5.28) 

2. X அச்சுக்கு இணையான நேர்க்கோட்டின் சமன்பாடு

(Equation of a straight line parallel to X axis)

AB என்ற நேர்க்கோடானது X அச்சுக்கு இணையாக, 'b' அலகு தொலைவில் உள்ளது என்க. AB-யின் மீதுள்ள ஒவ்வொரு புள்ளியின் y ஆயத் தொலைவு ‘b'-ஆக இருக்கும். (படம் 5.29) 

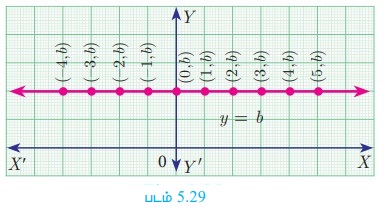
எனவே, AB -யின் சமன்பாடு y = b ஆகும். 

குறிப்பு

• b > 0 எனில், y = b எனும் கோடானது X அச்சுக்கு மேற்புறம் அமையும் 

• b < 0 எனில், y = b எனும் கோடானது X அச்சுக்கு கீழ்ப்புறம் அமையும் 

• b = 0 எனில், y = b எனும் கோடானது X அச்சு ஆகும்.

3. Y அச்சுக்கு இணையான நேர்க்கோட்டின் சமன்பாடு

(Equation of a Straight line parallel to the Y axis)

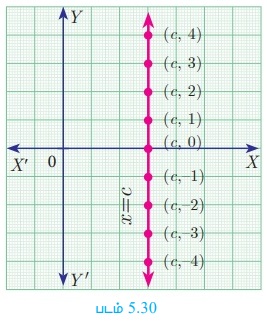
CD என்ற நேர்க்கோடானது Y அச்சுக்கு இணையாக, 'c' அலகு தூரத்தில் உள்ளது என்க. CD - யின் மீதுள்ள ஒவ்வொரு புள்ளியின் x-ன் ஆயத் தொலைவு ‘c’ ஆக இருக்கும். எனவே CD-யின் சமன்பாடு x = c ஆகும். (படம் 5.30).

குறிப்பு 

· c > 0 எனில், x = c எனும் கோடானது Y அச்சுக்கு வலப்பக்கம்

அமையும். 

· c < 0 எனில், x = c எனும் கோடானது Y அச்சுக்கு இடப்பக்கம்

அமையும். 

· c = 0 எனில், x = c எனும் கோடானது Y அச்சு ஆகும்.

எடுத்துக்காட்டு 5.17 

(5,7) என்ற புள்ளி வழி செல்வதும் (i) X அச்சுக்கு இணையாகவும் (ii) Y அச்சுக்கு இணையாகவும் அமைந்த நேர்க்கோட்டின் சமன்பாட்டைக் காண்க. 

தீர்வு 

(i) X அச்சுக்கு இணையான நேர்க்கோட்டின் சமன்பாடு y=b.

இது (5,7) வழி செல்வதால், b = 7.

எனவே, தேவையான நேர்க்கோட்டின் சமன்பாடு y=7.. 

(ii) Y அச்சுக்கு இணையான நேர்க்கோட்டின் சமன்பாடு x=c

இது (5,7) வழி செல்வதால், c = 5

எனவே, தேவையான நேர்க்கோட்டின் சமன்பாடு x=5. 

4. சாய்வு- வெட்டுத்துண்டு வடிவம் (Slope-Intercept Form)

நேர்குத்தற்ற அனைத்து நேர்க்கோடுகளும் Y அச்சை ஒரு புள்ளியில் வெட்டும். இப்புள்ளியின் y ஆயத்தொலைவை y வெட்டுத்துண்டு என்று அழைக்கிறோம். ஒரு கோட்டின் சாய்வு m மற்றும் y வெட்டுத்துண்டு c எனில், அந்த நேர்க்கோட்டின் சமன்பாடு y = mx+c.

இச்சமன்பாடு சாய்வு- வெட்டுத்துண்டு வடிவம் ஆகும்.

உங்களுக்குத் தெரியுமா?

· ஒரு கோட்டின் சாய்வு m, m≠0 மற்றும் x வெட்டுத்துண்டு d எனில், அந்த நேர்க்கோட்டின் சமன்பாடு y = m (x-d). 

· சாய்வு m உடைய ஆதிப்புள்ளி வழிச் செல்லும் நேர்க்கோட்டின் சமன்பாடு y = mx.

எடுத்துக்காட்டு 5.18 

பின்வரும் விவரங்களைப் பயன்படுத்தி நேர்க்கோட்டின் சமன்பாடு காண்க.

(i) சாய்வு 5 மற்றும் y வெட்டுத்துண்டு -9 

(ii) சாய்வு கோணம் 45° மற்றும் y வெட்டுத்துண்டு 11 

தீர்வு 

(i) இங்கு சாய்வு = 5, y வெட்டுத்துண்டு c = -9 

எனவே, நேர்க்கோட்டின் சமன்பாடு y = mx + c

y = 5x − 9 ⇒ 5x − y − 9 = 0

(ii) இங்கு, θ = 45°, y வெட்டுத்துண்டு c = 11

சாய்வு m = tan θ = tan 45° = 1 

எனவே, நேர்க்கோட்டின் சமன்பாடு y = mx + c

y= x + 11 ⇒ x − y + 11 = 0

உங்களுக்குத் தெரியுமா?

xy தளத்தின் மீதுள்ள (x, y) எனும் புள்ளியில் x என்பது “கிடைஅச்சு தொலைவு” (Abscissa) என்றும் y என்பது "செங்குத்து அச்சு தொலைவு” (Ordinate) என்றும் அழைக்கப்படுகிறது.

எடுத்துக்காட்டு 5.19 

8x − 7y + 6 = 0 என்ற கோட்டின் சாய்வு மற்றும் y வெட்டுத்துண்டு ஆகியவற்றைக் கணக்கிடுக. 

தீர்வு 

கொடுக்கப்பட்ட நேர்க்கோட்டின் சமன்பாடு 8x − 7y + 6 = 0 

7y = 8x + 6 (இதனை y = mx +c வடிவத்திற்கு மாற்றவும்)

 y = 8/7 x + 6/7 …(1)

(1) ஐ y = mx +c உடன் ஒப்பிட,

சாய்வு m = 8/7 மற்றும் y வெட்டுத்துண்டு c = 6/7

எடுத்துக்காட்டு 5.20 

வரைபடமானது y அச்சில் பாரன்ஹீட் டிகிரி வெப்பநிலையையும் x அச்சில் செல்சியஸ் டிகிரி வெப்பநிலையையும் குறிக்கிறது எனில், (a) கோட்டின் சாய்வு மற்றும் y வெட்டுத்துண்டு காண்க. (b) கோட்டின் சமன்பாட்டை எழுதுக. (c) பூமியின் சராசரி வெப்பநிலை 25° செல்சியஸாக இருக்கும்போது பூமியின் சராசரி வெப்பநிலையைப் பாரன்ஹீட்டில் காணவும். 

தீர்வு 

(a) படத்திலிருந்து. சாய்வு

கோடானது y அச்சினை (0, 32) -யில் சந்திக்கிறது. 

ஆகையால் சாய்வு 9/5 மற்றும் y வெட்டுத்துண்டு 32 ஆகும். 

(b) சாய்வு மற்றும் y வெட்டுத்துண்டு வடிவத்தைப் பயன்படுத்தி, நேர்க்கோட்டின் சமன்பாட்டை எழுதலாம். 

நேர்க்கோட்டின் சமன்பாடு y = 9/5 x + 32 

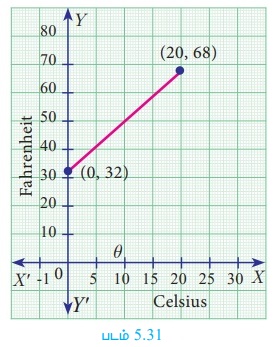
(c) பூமியின் சராசரி வெப்பநிலை 25° செல்சியஸ் ஆக இருக்கும்போது y-ஐ பாரன்ஹீட் டிகிரியில் காண x = 25 எனக் கொள்க.

y = 9/5 x + 32

y = 9/5 (25) + 32

y = 77

எனவே, பூமியின் சராசரி வெப்பநிலை 77° F ஆகும். 

குறிப்பு 

செல்சியஸைப் பாரன்ஹீட்டாக மாற்றத் தேவையான சூத்திரம் F = 9/5 C + 32 ஆகும். இந்த எடுத்துக்காட்டின் மூலம் ஒரு நேர்க்கோட்டினை ஒரு நேரிய சமன்பாடாக எழுதமுடியும் என அறிகிறோம்.

5. புள்ளி - சாய்வு வடிவம் (Point-Slope form)

A(x1 , y1 ) என்ற புள்ளி வழியாகச் செல்வதும் மற்றும் சாய்வு m உடையதுமான ஒரு நேர்க்கோட்டின் சமன்பாட்டைக் காண்போம். 

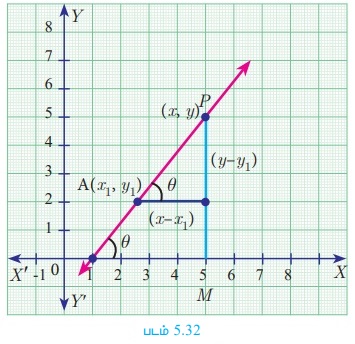
கோட்டின்மீது A இல்லாத மற்றொரு புள்ளி P (x, y) என்க.

A(x1 , y1 ) மற்றும் P (x, y) என்ற புள்ளிகளை இணைக்கும் கோட்டின் சாய்வு

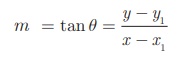
எனவே, தேவையான நேர்க்கோட்டின் சமன்பாடு y − y1 = m (x − x1) (புள்ளி- சாய்வு வடிவம்)

எடுத்துக்காட்டு 5.21 

(3, -4) என்ற புள்ளியின் வழி செல்வதும், -5/7 -ஐ சாய்வாக உடையதுமான நேர்க்கோட்டின் சமன்பாட்டைக் காண்க.

தீர்வு 

(x1, y1 ) = (3, −4)  மற்றும் m = −5/7 எனக் கொடுக்கப்பட்டுள்ளது.

புள்ளி-சாய்வு வடிவில் நேர்க்கோட்டின் சமன்பாடு

y − y1 = m (x − x1)

y + 4 = − 5/7 (x - 3)

இதிலிருந்து 5x + 7y + 13 = 0

சிந்தனைக் களம் 

Y அச்சுக்கு இணையாக இருக்கும் நேர்க்கோட்டினைச் சாய்வு - வெட்டுத் துண்டு வடிவில் எழுத முடியுமா?

எடுத்துக்காட்டு 5.22 

(2, 5) மற்றும் (4,7) என்ற புள்ளிகளைச் சேர்க்கும் நேர்க்கோட்டிற்குச் செங்குத்தாகவும், A(1, 4) என்ற புள்ளி வழி செல்லுவதுமான நேர்க்கோட்டின் சமன்பாட்டைக் காண்க.

தீர்வு 

கொடுக்கப்பட்ட புள்ளிகள் A(1, 4), B(2,5) மற்றும் C(4,7).

BC -யின் சாய்வு = (7–5) / (4-2) = 2/2 = 1 

தேவையான நேர்க்கோட்டின் சாய்வு m என்க.

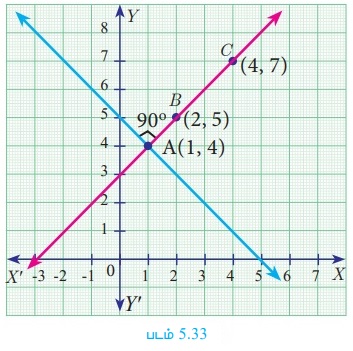
இந்த நேர்க்கோடு BC-க்கு செங்குத்தாக உள்ளது. 

எனவே, m ×1 = −1 

m = −1

இக்கோடானது A(1,4) வழி செல்வதால்,

தேவையான நேர்க்கோட்டின் சமன்பாடு y − y 1  = m (x − x1 )

y - 4 = −1(x −1)

y – 4 = −x + 1

எனவே, x + y – 5 = 0

உங்களுக்குத் தெரியுமா?

மாபெரும் கணிதவியல் மற்றும் இயற்பியல் மேதைகளாகத் திகழ்ந்த கலீலியோ மற்றும் நியூட்டன் போன்றோர் ஒரு தளம் மற்றும் வெளியில் பொருட்களின் இயக்கத்தை விவரிக்க ஆயத்தொலை வடிவியலைப் பயன்படுத்தியுள்ளனர்.

6. இரு புள்ளி வடிவம் (Two Point form)

A(x1 , y1 )  மற்றும் B (x2 , y2 ) என்பன இரு வெவ்வேறான புள்ளிகள் என்க. கொடுக்கப்பட்ட இந்த இரு புள்ளிகள் வழிச் செல்லும் நேர்க்கோட்டின் சாய்வு m =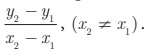 

புள்ளி - சாய்வு வடிவத்தின் மூலம், நேர்க்கோட்டின் சமன்பாடு

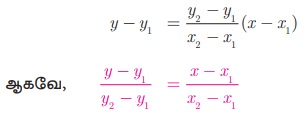
(இரு புள்ளி வடிவில் நேர்க்கோட்டின் சமன்பாடு ஆகும்) 

எடுத்துக்காட்டு 5.23 

(5, -3) மற்றும் (7, -4) என்ற இரு புள்ளிகள் வழிச் செல்லும் நேர்க்கோட்டின் சமன்பாடு காண்க. 

தீர்வு 

(x1 , y1) மற்றும் (x2 , y2) என்ற இரு புள்ளிகள் வழிச் செல்லும் நேர்க்கோட்டின் சமன்பாடு

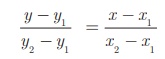
கொடுக்கப்பட்ட புள்ளிகளைப் பிரதியிட நாம் பெறுவது,

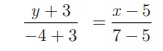
⇒ 2y + 6 = − x + 5

⸫ x + 2y + 1 = 0 என்பது தேவையான நேர்க்கோட்டின் சமன்பாடு ஆகும்.

எடுத்துக்காட்டு 5.24 

வெவ்வேறு உயரங்கள் கொண்ட இரண்டு கட்டடங்கள் ஒன்றுக்கொன்று எதிரெதிராக உள்ளன. ஒரு கனமான கம்பியானது கட்டடங்களின் மேற்புறங்களை (6,10) என்ற புள்ளியிலிருந்து (14,12) என்ற புள்ளி வரை இணைக்கிறது எனில், கம்பியின் சமன்பாட்டைக் காண்க. 

தீர்வு 

கட்டடங்களின் மேற்புறங்களில் உள்ள புள்ளிகள் A(6, 10) மற்றும் B(14, 12)  என்க. 

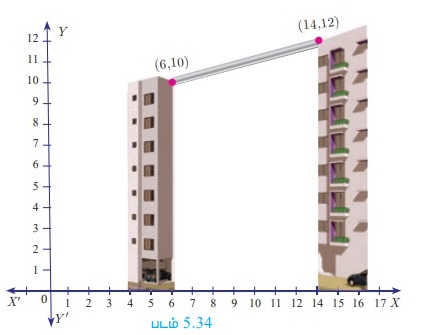
A(6, 10) மற்றும் B(14, 12)  என்ற புள்ளி வழிச் செல்லும் இரும்புக் கம்பியின் நேர்க்கோட்டுச் சமன்பாடு

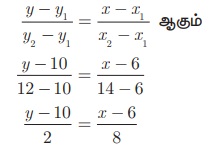
 எனவே, x − 4y + 34 = 0 ஆகவே, இரும்புக் கம்பியின் சமன்பாடு x − 4y + 34 = 0 

7. வெட்டுத்துண்டு வடிவம் (Intercept Form)

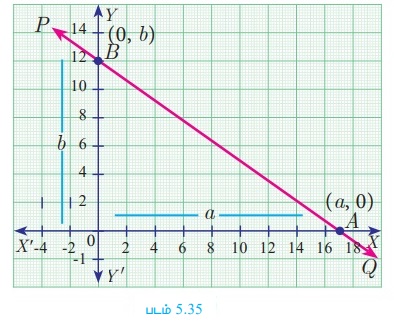
ஒரு நேர்க்கோடானது ஆய அச்சுகளில் முறையே a மற்றும் b என்ற வெட்டுத்துண்டுகளை ஏற்படுத்தினால், அந்நேர்க்கோட்டின் சமன்பாட்டை நாம் கண்டறியலாம்.

PQ என்ற நேர்க்கோடானது X அச்சை A-யிலும், Y அச்சை B-யிலும் சந்திக்கிறது. OA=a, OB=b என்க.

எனவே, A மற்றும் B-யின் ஆயப் புள்ளிகள் முறையே (a,0) மற்றும் (0, b) ஆகும். A மற்றும் B என்ற புள்ளிகளை இணைக்கும் கோட்டின் சமன்பாடு

முன்னேற்றச் சோதனை 

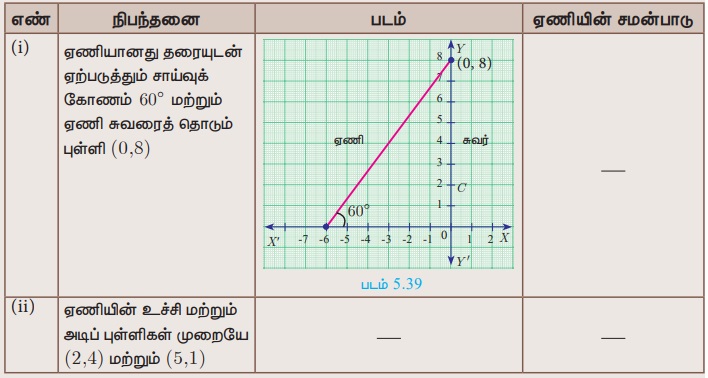
அட்டவணையில் விடுபட்ட இடங்களைப் பூர்த்தி செய்க. 

எடுத்துக்காட்டு 5.25 

ஆய அச்சுகளுடன் சமமாகவும், எதிர் குறியும் உடைய வெட்டுத்துண்டுகளை ஏற்படுத்தி, (5,7) என்ற புள்ளி வழி செல்லும் நேர்க்கோட்டின் சமன்பாட்டைக் காண்க 

தீர்வு 

x வெட்டுத்துண்டு a மற்றும் y - வெட்டுத்துண்டு ‘-a' என்க. 

வெட்டுத்துண்டு வடிவில் நேர்க்கோட்டின் சமன்பாடு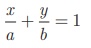

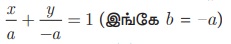
எனவே, x − y = a         ...(1) 

(1) ஆனது (5,7) வழிச் செல்வதால், 5 - 7 = a ⇒ a = -2 

ஆகவே, தேவையான நேர்க்கோட்டின் சமன்பாடு x − y = −2 அதாவது x − y + 2 = 0 

எடுத்துக்காட்டு 5.26 

4x − 9y + 36 = 0 என்ற நேர்க்கோடு ஆய அச்சுகளில் ஏற்படுத்தும் வெட்டுத்துண்டுகளைக் காண்க. 

தீர்வு 

கொடுக்கப்பட்ட நேர்க்கோட்டு சமன்பாடு 4x − 9y + 36 = 0 

எனவே 4x - 9y = −36

இருபுறமும் -36 ஆல் வகுக்க, 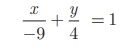 ...(1)

(1)-ஐ வெட்டுத்துண்டு வடிவத்துடன் ஒப்பிட, x-வெட்டுத்துண்டு a = -9; y - வெட்டுத்துண்டு b = 4 

எடுத்துக்காட்டு 5.27 

ஓர் அலைபேசி மின்கலத்தின் சக்தி 100% இருக்கும்போது (battery power) அலைபேசியைப் பயன்படுத்தத் தொடங்குகிறோம். x மணி நேரம் பயன்படுத்திய பிறகு மீதி இருக்கும் மின்கலத்தின் சக்தி y சதவீதம் (தசமத்தில்) ஆனது y = −0. 25x + 1 ஆகும். 

(i) எத்தனை மணி நேரத்திற்குப் பிறகு மின்கலத்தின் சக்தி 40% ஆகக் குறைந்திருக்கும் எனக் காண்க. 

(ii) மின்கலம் தனது முழுச் சக்தியை இழக்க எடுத்துக்கொள்ளும் கால அளவு எவ்வளவு? 

தீர்வு

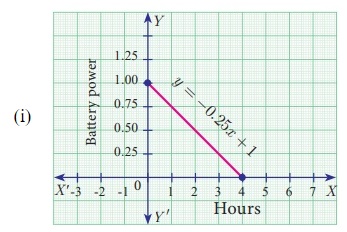
(i) மின்கலச் சக்தி 40% எனில், நேரத்தைக் கணக்கிட, y = 0.40 என எடுத்துக் கொள்க.

 0.40 = −0. 25x + 1 ⇒ 0. 25x = 0. 60

x = 0.60/0.25 = 2.4 மணி.

(ii) மின்கலம் தனது முழுச் சக்தியை இழந்துவிட்டால் y = 0 எனக் கிடைக்கும்.

எனவே, 0 = −0.25x + 1 ⇒ 0.25x = 1 எனவே, x = 4 மணி. 

⸫ நான்கு மணி நேரத்திற்குப் பின்பு அலைபேசியின் மின்கலம் தனது முழுச் சக்தியையும் இழக்கிறது. 

எடுத்துக்காட்டு 5.28 

(-3, 8) என்ற புள்ளிவழி செல்வதும், ஆய அச்சுகளின்மிகை வெட்டுத்துண்டுகளின் கூடுதல் 7 உடையதுமான நேர்க்கோட்டின் சமன்பாட்டைக் காண்க. 

தீர்வு 

a, b என்பன வெட்டுத்துண்டுகள் எனில் a + b = 7 அல்லது b = 7 – a

வெட்டுத்துண்டு வடிவம் x/a + y/b = 1

ஆகவே, x/a + y/(7−a) = 1

இக்கோடானது (-3,8), என்ற புள்ளி வழிச் செல்வதால் 

−3/a + 8/(7 – a) = 1  ⇒  –3(7–a) + 8a = a(7–a)

 − 21 + 3a + 8a = 7a −a2

ஆகவே, a 2 + 4a − 21 = 0 

இதனைத் தீர்ப்பதன் மூலம் (a − 3) (a + 7) = 0

a = 3 அல்லது a = −7

a என்பது மிகை எண் என்பதால் a = 3 மற்றும் b = 7 – a = 7–3 = 4.

எனவே, x/3 + y/4 = 1

ஆகவே, தேவையான நேர்க்கோட்டின் சமன்பாடு 4x + 3y −12 = 0 

எடுத்துக்காட்டு 5.29 

கிழக்கு நிழற்சாலை மற்றும் குறுக்குச் சாலைகளால் ஒரு வட்ட வடிவத் தோட்டம் சூழப்பட்டுள்ளது. குறுக்குச் சாலையானது வடக்கு தெருவை D-யிலும், கிழக்குச் சாலையை E-யிலும் சந்திக்கிறது. தோட்டத்திற்கு A(3,10) என்ற புள்ளியில் AD ஆனது தொடுகோடாக அமைகிறது. படத்தைப் பயன்படுத்தி 

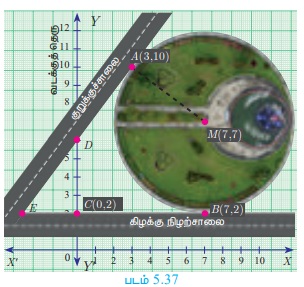
(a) பின்வருவனவற்றின் சமன்பாட்டினைக் காண்க 

(i) கிழக்கு நிழற்சாலை

(ii) வடக்குத் தெரு

(iii) குறுக்குச்சாலை

(b) குறுக்குச்சாலை கீழ்க்கண்டவற்றைச் சந்திக்கின்ற புள்ளியைக் காண்க 

(i) வடக்குத் தெரு

(ii) கிழக்கு நிழற்சாலை 

தீர்வு 

(a) (i) கிழக்கு நிழற்சாலையானது C(0, 2) மற்றும் B(7,2) என்ற புள்ளிகளை இணைக்கும் நேர்க்கோடாகும். 

எனவே இரு புள்ளி வடிவத்தைப் பயன்படுத்திக் கிழக்கு நிழற்சாலையின் சமன்பாடு,

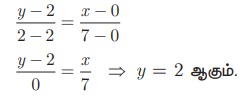
(ii) D மற்றும் C(0,2) என்ற புள்ளிகள் ஒரே நேர்க்கோட்டில் அமைகிறது எனில் புள்ளி D-யின் x ஆயத் தொலைவு = 0 ஆகும். 

ஆகவே, வடக்கு தெருவிலுள்ள எந்தப் புள்ளிக்கும் x-யின் ஆயத் தொலைவு = 0 ஆகும்

எனவே, வடக்கு தெருவின் சமன்பாடு x = 0. 

(iii) குறுக்குச் சாலையின் சமன்பாட்டைக் காணுதல்.

வட்டவடிவத் தோட்டத்தின் மையம் M-யின் ஆயப் புள்ளி (7,7) மற்றும் A- யின் ஆயப் புள்ளி (3,10) ஆகும். 

MA-யின் சாய்வு m1 எனில், m1 = (10 −7) / (3-7) = −3/4. 

குறுக்குச் சாலையானது MA-க்கு செங்குத்தாக உள்ளது. எனவே குறுக்குச் சாலையின் சாய்வு m2 எனில், m1m2  = −1 ⇒ −3/4 m2  = −1  ⸫,  m2  = 4/3. 

குறுக்குச் சாலையானது, சாய்வு 4/3 மற்றும் A (3,10) என்ற புள்ளி வழியாகவும் செல்கிறது 

எனவே, குறுக்குச் சாலையின் சமன்பாடு y − 10 = 4/3 (x − 3)

3y − 30 = 4x −12

4x − 3y + 18 = 0

(b) (i) குறுக்குச் சாலை மற்றும் வடக்குத் தெரு சந்திக்கும் புள்ளியைக் காணுதல்.

D(0, k) என்பது குறுக்குச் சாலையின் மேல் உள்ள புள்ளி ஆகும். எனவே, x = 0, y = k என குறுக்கு சாலையின் சமன்பாட்டில் பிரதியிட, நாம் பெறுவது 

0 − 3k + 18 = 0

⇒ k = 6 

எனவே, D ஆனது (0,6) ஆகும். 

(ii) குறுக்குச் சாலை மற்றும் கிழக்கு நிழற்சாலை சந்திக்கும் புள்ளியைக் காணுதல்.

E-யின் ஆயப் புள்ளி (q, 2) என்க. 

x = q, y = 2 எனக் குறுக்குச் சாலை சமன்பாட்டில் பிரதியிட,

4q − 6 + 18 = 0

4q = −12 எனவே q = –3

ஆகவே, E என்ற புள்ளி (-3,2) ஆகும்.

ஆதலால், குறுக்கு சாலையானது வடக்கு தெருவை D(0, 6) என்ற புள்ளியிலும், கிழக்கு நிழற்சாலையை E(-3, 2) என்ற புள்ளியிலும் சந்திக்கிறது.

முன்னேற்றச் சோதனை 

விடுப்பட்ட பகுதியை பூர்த்தி செய்க

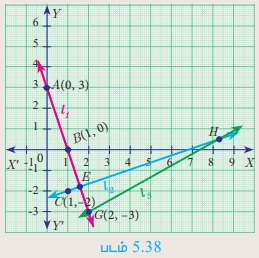
செயல்பாடு 4

l1 மற்றும் l2 என்ற கோடுகள் செங்குத்தானவை. கோடு l3 -யின் சாய்வு 3 எனில்,

(i) l1 என்ற கோட்டின் சமன்பாட்டைக் காண்க.

(ii) l2 கோட்டின் சமன்பாட்டைக் காண்க.

(iii) l3 என்ற கோட்டின் சமன்பாட்டைக் காண்க.

செயல்பாடு 5 

ஓர் ஏணியானது செங்குத்துச் சுவரின் மீது அதன் அடிப்பகுதி தரையைத் தொடுமாறு சாய்த்து வைக்கப்பட்டுள்ளது. கீழே கொடுக்கப்பட்ட நிபந்தனைகளின்படி ஏணியின் சமன்பாட்டைக் காண்க.