கூட்டுச் சராசரி (Arithmetic Mean)

கூட்டுச் சராசரி (Arithmetic Mean)

1. கூட்டுச் சராசரி – செப்பனிடப்படாத தரவுகள் (Arithmetic Mean −Raw Data)

எல்லாவகையான சராசரிகளிலும், பொதுவாகக் கொடுக்கப்பட்ட தகவலின் கூட்டுச்சராசரியே பயன்படுத்தப்படுகிறது. இது கொடுக்கப்பட்ட அனைத்து மதிப்புகளின் கூடுதலை, மதிப்புகளின் எண்ணிக்கையால் வகுத்துப் பெறப்படுகிறது.

எடுத்துக்காட்டாக, ஒரு (T20) மட்டைப் பந்தாட்ட வீரர் விளையாடிய 8 ஆட்டங்களில் எடுத்த ஓட்டங்கள் 25, 32, 36, 38, 45 , 41 , 35 மற்றும் 36 என எடுத்துக்கொண்டால், அவரின் சராசரியை,

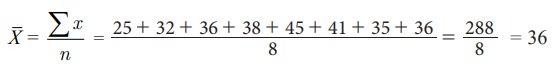 எனக் கணக்கிடலாம்.

இதையே x₁, x₂, x₃ … ,x_n என்ற n. மதிப்புகள் எனில் அவற்றின் கூட்டுச்சராசரி  ஐக் (X bar எனப் படிக்க வேண்டும்) கீழ்க்கண்டவாறு நாம் எழுதலாம்.

இவ்வாய்ப்பட்டை நாம் இவ்வாறாக எழுதலாம்:

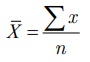
குறிப்பு

எந்த மதிப்பை நாம் ஊகச்சராசரியாகத் தேர்ந்தெடுக்கிறோம் என்பது ஒரு பொருட்டல்ல. அந்த ஊகச்சராசரி நம் கணக்கீட்டை எளிமைப்படுத்த வேண்டும். ஊகச்சராசரியாகத் தேர்ந்தெடுக்கும் எண் பெரும்பாலான மதிப்புகளுக்கு அருகாமையில் இருப்பின் நன்று. மேலும் அவ்வெண் கொடுக்கப்பட்ட பட்டியலில்தான் இருக்கவேண்டும் என்ற அவசியமில்லை.

ஊகச் சராசரி முறை (Assumed Mean method)

சில நேரங்களில், நம் கணக்கீட்டை எளிமையாகச் செய்வதற்கு ஒரு தோராயமான மதிப்பைச் சராசரியாகக் கணித்துக் கணக்கைச் செய்திருப்போம். அந்தத் தோராயமான மதிப்பை நாம் ஊகச்சராசரி என அழைக்கலாம். உதாரணமாக, முந்தைய எடுத்துக்காட்டில் உள்ள மட்டைப்பந்தாட்ட வீரர் எடுத்த ஓட்டங்களின் எண்ணிக்கையில் 38 என்ற மதிப்பை நாம் ஊகச்சராசரியாக எடுத்துக்கொள்வோம். பிறகு ஊகச்சராசரியிலிருந்து ஒவ்வொரு மதிப்பும் எவ்வளவு வேறுபடுகிறது என்பதைப் பட்டியலிடுவோம்.

25  − 38 =  −13,  32 − 38 =  −6,  36 − 38 =  −2,  38  − 38 = 0,  

45  − 38 = 7, 41  − 38 = 3,  35  − 38 =  −3,  36  − 38 =  −2

வேறுபாடுகளின் சராசரி = ( −13 – 6  − 2 + 0 +7 + 3 – 3 – 2) / 8 =  −16 / 8  =  − 2

இப்பொழுது ஊகச்சராசரியுடன் வேறுபாடுகளின் சராசரியைக் கூட்ட நமக்குச் சரியான சராசரி கிடைக்கும்.

எனவே, சரியான சராசரி = ஊகச்சராசரி + வேறுபாடுகளின் சராசரி = 38  − 2 = 36 .

பெரிய மதிப்பிலான எண்களுக்குச் சராசரி காண இந்த ஊகச்சராசரி முறை பயனுள்ளதாக இருக்கும்.

2. சராசரி  − வகைப்படுத்தப்படாத நிகழ்வெண் பரவல் (Mean −Ungrouped Frequency Distribution)

பள்ளி விளையாட்டு நிகழ்வில் பங்குகொண்ட 12 மாணவர்களின் உயரங்களை (சென்டி மீட்டரில்) எடுத்துக்கொள்வோம்.

140, 142, 150, 150, 140, 148, 140, 147, 145, 140, 147, 145.

இத்தரவுகளின் சராசரி உயரத்தை எவ்வாறு காண்பது?

இதற்குப் பல வழிகள் உள்ளன.

(i) அனைத்து மதிப்புகளையும் கூட்டி அதனை எண்ணிக்கையால் வகுத்துப் பெறலாம்.

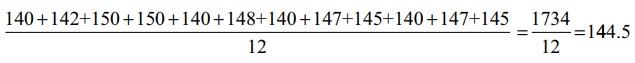
(ii) ஊகச்சராசரி முறையைப் பயன்படுத்தியும் பெறலாம். இங்கு 141 என்ற மதிப்பை ஊகச்சராசரியாக எடுத்துக்கொண்டு பின்வருமாறு சராசரி காணலாம்.

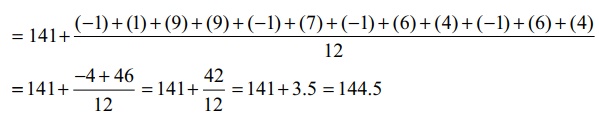
(iii) இம்மூன்றாவது முறையானது வகைப்படுத்தப்படாத நிகழ்வெண் பரவலுக்குச் சராசரி காணும் முறையை விளக்குகிறது. இங்கு 140 என்ற மதிப்பு 4 முறை வந்துள்ளது. எனவே 140 இன் நிகழ்வெண் 4. 142 என்ற மதிப்பு 1 முறை வந்துள்ளது. எனவே 142 இன் நிகழ்வெண் 1. இதைப் போன்றே மற்ற மதிப்புகளுக்கும் காணும் போது, நமக்கு பின்வரும் நிகழ்வெண் பட்டியல் கிடைக்கின்றது.

இங்கு 140, 4 முறை இருப்பதைக் காணலாம். அதன் மொத்தம் 140 × 4 = 560

இங்கு 142, 1 முறை இருப்பதைக் காணலாம். அதன் மொத்தம் 142 × 1 = 142

இங்கு 150, 2 முறை இருப்பதைக் காணலாம். அதன் மொத்தம் 150 × 2 = 300.

இதைப்போலவே மற்ற மதிப்புகளையும் காணவேண்டும்.

இத்தரவுகளைக் பின்வருமாறு பட்டியலிடலாம்.

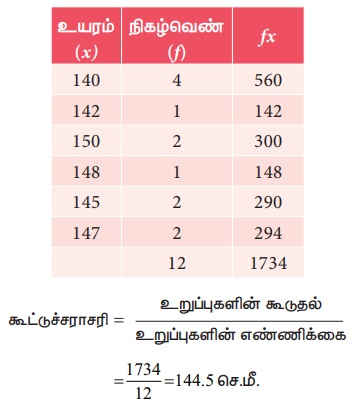
கூட்டுச்சராசரி = உறுப்புகளின் கூடுதல் / உறுப்புகளின் எண்ணிக்கை

 = 1734 / 12

= 144.5 செ.மீ.

இம்முறையை அனைத்துத் தரவுகளுக்கும் பொதுமைப்படுத்தலாம். இது ஒரு வாய்ப்பாடாகவும் உருவாகிறது. x₁, x₂, x_{3 ,}… ,x_n என்ற n விவரங்களின் நிகழ்வெண்கள் முறையே f₁, f₂, f₃,..., f_n எனில், சராசரி ஆனது பின்வருமாறு கிடைக்கிறது.

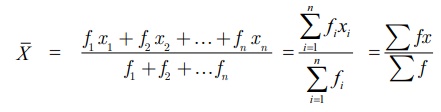
மேற்காணும் முறையை ஊகச்சராசரி முறையுடன் இணைத்துப் பயன்படுத்த இயலுமா? இதோ அதை நோக்கிய ஒரு முயற்சி!

குறிப்பு

ஒவ்வொரு படிநிலையிலும் உள்ள அனைத்துக் குறியீடுகளும் எதனைக் குறிக்கின்றன என்பதன் பொருளுணர்ந்து அதனை முழுமையாகப் புரிந்து படிக்க வேண்டும்

(iv) ஊகச்சராசரி 145 என்க. இப்பொழுது கீழ்க்காணும் அட்டவணையைத் தயார் செய்வோம்

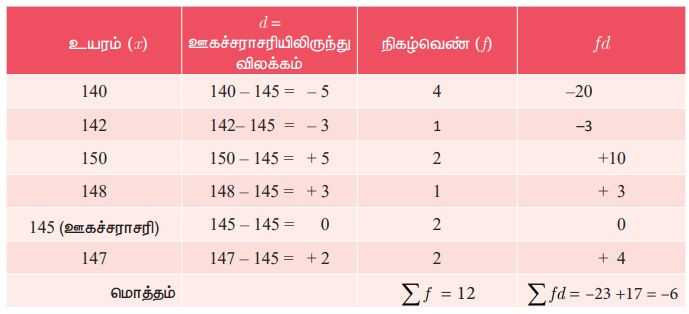
கூட்டுச் சராசரி = ஊகச்சராசரி + விலக்கங்களின் கூடுதல்களின் சராசரி

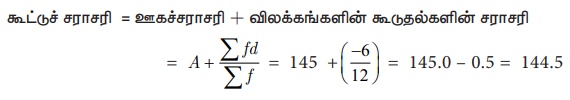
பெரிய மதிப்பிலான எண்களுக்குச் சராசரி காண இந்த ஊகச்சராசரி முறை உதவியாக இருக்கும்.

3. சராசரி − வகைப்படுத்தப்பட்ட நிகழ்வெண் பரவல் (Mean −Grouped Frequency Distribution)

கொடுக்கப்பட்ட தரவுகளைப் பிரிவு இடைவெளிகளாகவும் மற்றும் அதிர்வெண் பட்டியலாகவும் வகைப்படுத்தி கீழ்க்கண்டவாறு நிகழ்வெண் பட்டியலை உருவாக்கலாம்

மேற்கண்ட பட்டியலானது பல்வேறு வயதுடைய வாடிக்கையாளர்களின் எண்ணிக்கையைக் காட்டுகிறது. எடுத்துக்காட்டாக, 120 வாடிக்கையாளர்கள் 20 முதல் 30 வயதுக்குட்பட்டவர்களாக இருக்கிறார்கள். (வகைப்படுத்தப்பட்ட நிகழ்வெண் அட்டவணை தயாரிக்கும் போது தனிப்பட்ட தரவுகள் மறைந்து போகும்) இப்போது ஒவ்வொரு பிரிவு இடைவெளியின் பிரதிநிதியாகச் செயல்பட ஒரு மதிப்பு தேவைப்படுகின்றது. இது அந்தப் பிரிவின் மைய மதிப்பாகும்.

மையப்புள்ளி (அ) பிரிவுப் புள்ளியானது கீழ்க்காணும் வாய்ப்பாடு மூலம் கணக்கிடப்படுகிறது..

பிரிவின் மையப்புள்ளி = ( UCL + LCL) / 2 

இங்கு UCL  − என்பது பிரிவின் மேல் எல்லை , LCL − என்பது பிரிவின் கீழ் எல்லை ஆகும்.

தொகுக்கப்பட்ட நிகழ்வெண் பரவலின் சராசரியைக் கீழ்க்காணும் முறைகளில் ஏதேனும் ஒரு முறையைப் பயன்படுத்திக் கணக்கிடலாம்:

(i) நேரடி முறை

(ii) ஊகச் சராசரி முறை

(iii) படிவிலக்க முறை

(i) நேரடி முறை (Direct Method)

நேரடி முறையைப் பயன்படுத்தும் போது, சராசரி காண்பதற்கான வாய்ப்பாடு

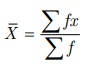
இங்கு x என்பது பிரிவு இடைவெளியின் மையப்புள்ளி மற்றும் f என்பது அந்தப் பிரிவு இடைவெளியின் நிகழ்வெண் ஆகும்.

நேரடி முறையில் சராசரி காண்பதற்கான படிகள் :

i) ஒவ்வொரு பிரிவு இடைவெளியின் மையப்புள்ளியைக் கண்டுபிடித்து அதை x எனக் குறிக்கவும்.

(ii) இம் மையப்புள்ளிகளை அதற்குரிய பிரிவு இடைவெளியின் நிகழ்வெண்ணோடு பெருக்கி, அப்பெருக்கல் பலனின் கூடுதல் fx ஐக் காணவும்.

(iii) ∑fx ஐக் நிகழ்வெண்களின் ∑f ஆல் வகுக்க, சராசரி கிடைக்கும்.

எடுத்துக்காட்டு 8.1

ஒரு குடியிருப்பில் வாழும் மக்களின் எண்ணிக்கை வயதின் அடிப்படையில் கொடுக்கப்பட்டுள்ளது. குடியிருப்பில் வாழும் மக்களின் சராசரி வயதைக் காண்க.

தீர்வு

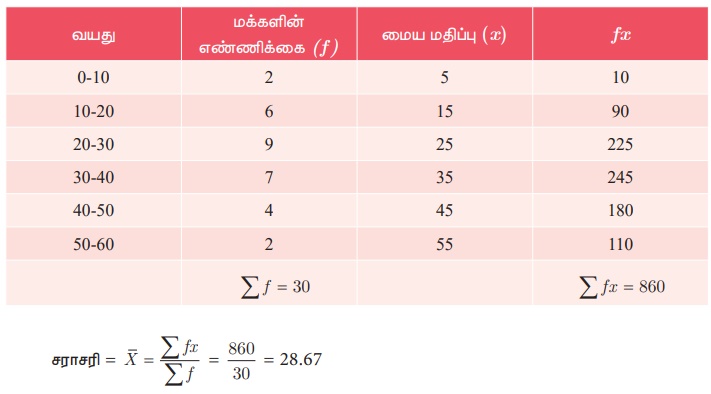
குடியிருப்பில் வாழும் மக்களின் சராசரி வயது = 28.67.

(ii) ஊகச் சராசரி முறை (Assumed Mean Method)

வகைப்படுத்தப்பட்ட தரவுகளின் கூட்டுச் சராசரியை நேரடி முறையின் மூலம் விரைவாகக் காண்பதைப் பற்றிப் பார்த்தோம். கொடுக்கப்பட்ட தரவுகள் அதிக எண்ணிக்கையில் இருக்கும்போது தரவுகளையும் அதற்கான நிகழ்வெண்களையும் பெருக்கி மற்றும் அதனைக் கூட்டி மதிப்பு காண்பது கடினமாக இருப்பதோடு மட்டுமல்லாமல் தவறுகள் ஏற்படவும் அதிக நேரம் எடுத்துக்கொள்ளக் கூடியதாகவும் இருக்கும். இம்மாதிரியான வகைப்படுத்தப்பட்ட தரவுகளுக்கு ஊகச் சராசரி முறையைப் பயன்படுத்திக் கூட்டுச்சராசரி காணலாம்.

ஊகச் சராசரி முறையில் சராசரி காண்பதற்கான படிகள் :

1. தரவுகளில் ஏதாவது ஒரு மதிப்பை ஊகச் சராசரி (A) என எடுத்துக்கொள்வோம். அந்த மதிப்பானது மைய மதிப்பாக இருந்தால் சிறப்பானதாக இருக்கும்

2. ஒவ்வொரு பிரிவிற்கும் விலக்கம் d = x − A ஐக் காண்க.

3. விலக்கத்தினை அந்தந்தப் பிரிவு இடைவெளியின் நிகழ்வெண் f −உடன் பெருக்கி, பின்பு ∑fd ஐக் காண்க.

4. சராசரி 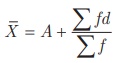என்ற வாய்ப்பாட்டைப் பயன்படுத்துக.

எடுத்துக்காட்டு 8.2

கீழ்க்காணும் தரவுகளுக்குச் சராசரியைக் காண்க.

தீர்வு

ஊகச் சராசரி A = 170

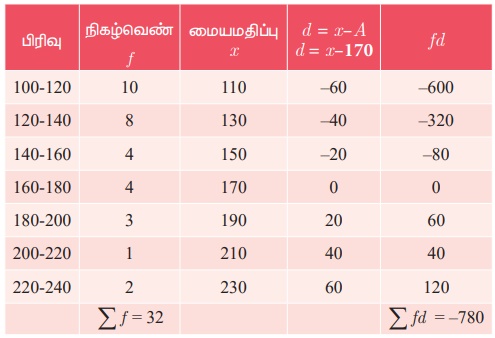
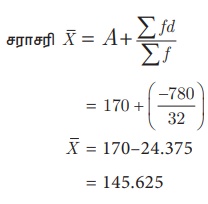
= 145.625

(iii) படிவிலக்க முறை (Step Deviation Method)

இம்முறையில், கணக்கிடுவதை எளிமைப்படுத்துவதற்காக விலக்கம் d = x  − A -ஐ இடைவெளியின் நீளம் c ஆல் வகுத்து (அதாவது ( x − A) / c) 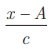 பின்பு c ஆல் பெருக்கி சராசரி காணும் வாய்ப்பாடு பின்வருமாறு பெறப்படுகின்றது:

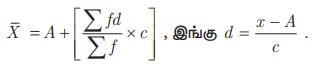
எடுத்துக்காட்டு 8.3

கீழ்க்காணும் பரவலிற்கு, படிவிலக்க முறையில், சராசரியைக் காண்க.

தீர்வு:

ஊகச் சராசரி A = 28, பிரிவு நீளம் c = 8

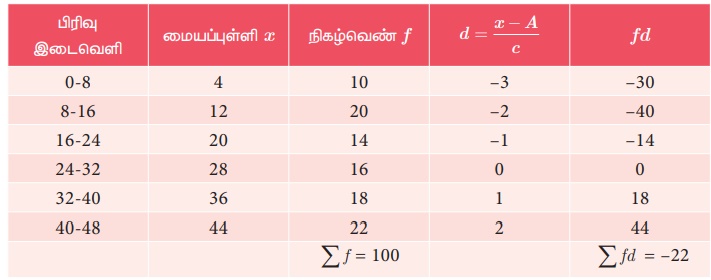
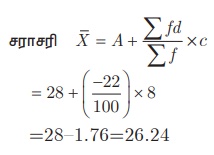
= 28  − 1.76 = 26.24

குறிப்பு

• x_i மற்றும் f_i  −ன் மதிப்பு சிறியதாக இருக்கும் போது நேரடி முறையே சிறந்தது.

• x_i மற்றும் f_i  −ன் மதிப்பு பெரியதாக இருக்கும் போது ஊகச் சராசரி அல்லது படிவிலக்க முறையைப் பயன்படுத்தலாம்

• பிரிவு இடைவெளிகள் சமமில்லாமல் இருக்கும் போதும், அது எண் மதிப்பில் பெரியதாக இருக்கும் போதும் படிவிலக்க முறையைப் பயன்படுத்தலாம்.

4. கூட்டுச்சராசரியின் சிறப்புப் பண்பு (A special property of the Arithmetic Mean)

1. சராசரியிலிருந்து, அனைத்து உறுப்புகளின் விலக்கங்களின் கூடுதல் பூச்சியம் ஆகும்.

x₁, x₂, x₃ … ,x_n என்ற n புள்ளிவிவரங்களின் கூட்டுச்சராசரி  எனில் 

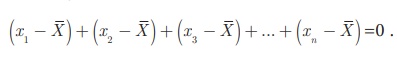
எனவே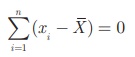

2. தரவிலுள்ள ஒவ்வொரு உறுப்புடனும் ஒரு மாறா மதிப்பு k ஐ கூட்டினாலோ அல்லது கழித்தாலோ முறையே அதன் சராசரியும் மாறா மதிப்பு k அளவு கூடும் அல்லது குறையும்.

3. தரவிலுள்ள ஒவ்வொரு உறுப்புடனும் ஒரு மாறா மதிப்பு k, k ≠ 0 ஆல் பெருக்கினாலோ அல்லது வகுத்தாலோ முறையே அதன் சராசரியும் மாறா மதிப்பு k ஆல் பெருக்கப்படும் அல்லது வகுக்கப்படும்.

எடுத்துக்காட்டு 8.4

கீழ்க்காணும் தரவுகளுக்குக் கூட்டுச் சராசரியிலிருந்து, விலக்கங்களின் கூட்டுத்தொகை காண்க. 21, 30, 22, 16, 24, 28, 18, 17

தீர்வு

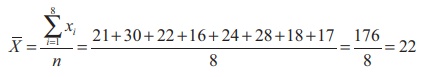
கூட்டுச்சராசரி லிருந்து x_i இன் விலக்கம் x_i – , i = 1, 2,….8 ஆகும்.

விலக்கங்களின் கூட்டுத்தொகை

= (21 −22) + (30  − 22) + (22  − 22) + (16  − 22) + (24  − 22) + (28  − 22) + (18  − 22) + (17  − 22)

= 16  − 16 = 0. அல்லது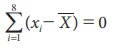 

எனவே, சராசரியிலிருந்து அனைத்து உறுப்புகளின் விலக்கங்களின் கூட்டுத்தொகை பூச்சியம் என அறியப்படுகின்றது.

முன்னேற்றத்தைச் சோதித்தல்

10 தரவுகளின் சராசரி 48 ஒவ்வொரு தரவுடனும் 7 ஐக் கழித்தால் கிடைக்கும் புதிய தரவுகளின் சராசரியைக் காண்க

எடுத்துக்காட்டு 8.5

6 தரவுகளின் சராசரி 45, ஒவ்வொரு தரவுடன் 4 ஐக் கூட்டினால் கிடைக்கும் சராசரியைக் காண்க

தீர்வு

x₁, x₂, x₃, x₄ , x₅ , x₆ என்ற தரவுகளின்

சராசரி 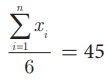 என்க.

ஒவ்வொரு தரவுடன் 4 ஐக் கூட்டினால் கிடைக்கும் புதிய சராசரி,

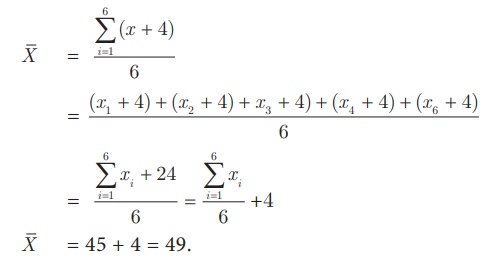
முன்னேற்றத்தைச் சோதித்தல்

• 12 தரவுகளின் சராசரி 20 ஒவ்வொரு தரவையும் 6 ஆல் பெருக்க கிடைக்கும் புதிய தரவுகளின் சராசரியைக் காண்க.

• 30 தரவுகளின் சராசரி 16 ஒவ்வொரு தரவையும் 4 ஆல் வகுக்கக் கிடைக்கும் புதிய தரவுகளின் சராசரியைக் காண்க.

எடுத்துக்காட்டு 8.6

7 தரவுகளின் சராசரி 30 என்க ஒவ்வோர் எண்ணையும் 3 ஆல் வகுக்கக் கிடைக்கும் புதிய சராசரியைக் காண்க.

தீர்வு

X என்பது x₁, x₂, x₃, x₄ , x₅ , x₆ , x₇ என்ற 7 தரவுகள் அடங்கியது எனில்

ஒவ்வோர் எண்ணையும் 3 ஆல் வகுக்கக் கிடைக்கும் புதிய சராசரி

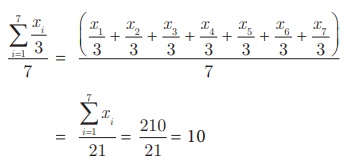
மாற்று முறை

Y என்பது X இன் ஒவ்வோர் எண்ணையும் 3 ஆல் வகுக்கக் கிடைக்கும் மதிப்பு எனில்

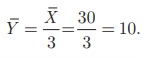
முன்னேற்றத்தைச் சோதித்தல்

நான்கு எண்கள் மதிப்புகளில் கொடுக்கப்பட்டுள்ளன. ஒவ்வொரு எண்ணையும் விடுத்துக் கிடைக்கும் மற்ற மூன்று எண்களின் கூட்டுச்சராசரிகள் முறையே 45, 60, 65 அல்லது 70 எனில், அந்த நான்கு எண்களின் கூட்டுச்சராசரியைக் காண்க.

எடுத்துக்காட்டு 8.7

25 மாணவர்களின் சராசரி மதிப்பெண் 78.4. இங்கு 96 என்ற மதிப்பானது 69 எனத் தவறுதலாக எடுக்கப்பட்டது கண்டறியப்பட்டது எனில், மதிப்பெண்களுக்கான சரியான சராசரியைக் காண்க.

தீர்வு

மாணவர்களின் எண்ணிக்கை மற்றும் சராசரி முறையே n = 25,  = 78.4

தவறான ∑x =  × n = 78.4 × 25 = 1960

சரியான ∑x = தவறான ∑x  − தவறான மதிப்பெண் + சரியான மதிப்பெண்

= 1960 – 69 + 96 = 1987

சரியான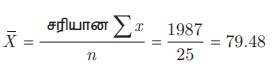

 = 79.48