இடைநிலை அளவு (Median)

இடைநிலை அளவு (Median)

தரவுகளில் அதிக மதிப்புடைய தரவின் மதிப்பைக் குறைத்து, குறை மதிப்புடைய தரவின் மதிப்பை அதிகரித்துச் சரிசமமாகச் சமநிலைப்படுத்தும் தனித்துவமான மையமதிப்பு கூட்டுச் சராசரி ஆகும். ஓர் அலுவலகத்தில் பணிபுரியும் நான்கு பேரின் வருமானங்கள் முறையே ₹5000, ₹6000, ₹7000 மற்றும் ₹8000 என எடுத்துக்கொண்டால் அவர்களின் சராசரி வருமானம் = (5000+6000+7000+8000 ) / 4 = ₹6500 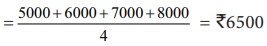ஆகும். இப்போது ஐந்தாவதாக ஒருவர் ₹29000 மாத வருமானத்தில் இக்குழுவில் சேர்ந்தால், இந்த ஐந்து நபர்களின் சராசரி வருமானம் ( 5000+ 6000+7000+ 8000 + 29000 ) / 5 = 55000 / 5 = ₹11000 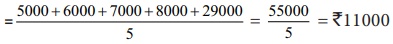 ஆகும். இத்தரவுகளிலிருந்து குழுவில் உள்ள ஒவ்வொருவரின் சராசரி வருமானம் ₹11000 எனக் கூற இயலுமா? இது தவறாக அமைந்து விடாதா? இங்கே உள்ள சிக்கல் என்னவெனில் மிக உயர்ந்த மதிப்பானது சராசரியைப் பாதிக்கிறது. மேலும் அது சராசரியை பொதுவான மைய மதிப்பிலிருந்து விலக்கிச் செல்கிறது. இது போன்ற நிகழ்வில் நாம் மாறுபட்ட சராசரி வகையைத் தேர்ந்தெடுப்பது அவசியமாகிறது.

இடைநிலை அளவு

எடுத்துக்காட்டாக, ஒரு வகுப்பில் உள்ள 9 மாணவர்களின் உயரங்கள் முறையே 122 செ.மீ, 138 செ.மீ, 124 செ.மீ, 125 செ.மீ, 135 செ.மீ, 141 செ.மீ, 138 செ.மீ, 140 செ.மீ, 141 செ.மீ, 147 செ.மீ, மற்றும் 161 செ.மீ. என எடுத்துக்கொள்வோம்.

(i) வழக்கமான கணக்கீட்டில் சராசரி 137செ.மீ ஆகும்.

(ii) அந்த உயரங்களை ஏறு வரிசையில் 122 செ.மீ, 125 செ.மீ, 125 செ.மீ, 135 செ.மீ, 138 செ.மீ, 140 செ.மீ, 141 செ.மீ, 147 செ.மீ, 160 செ.மீ என எழுதும்போது 138 செ.மீ என்ற மதிப்பானது இருபுறமும் சம அளவிலான எண்ணிக்கையில் உறுப்புகள் இருப்பதைக் காணலாம். அந்த மதிப்பை அவ்வுயரங்களின் இடைநிலை அளவு என்கிறோம்.

(iii) ஒரு தரவுத்தொகுப்பில் 11 உறுப்புகள் ஒரு வரிசையில் அமைந்து இருந்தால், அதன் 6 வது உறுப்பு இடைநிலை அளவு ஆகும். ஏனெனில் அவ்வுறுப்பு தான் மையத்தில் உள்ளது. தரவுத்தொகுப்பில் 101 உறுப்புகள் இருந்தால் 51 −வது உறுப்பு இடைநிலை அளவு ஆகும்.

ஒரு தரவுத்தொகுப்பில் ஒற்றை எண்ணிக்கையில் உறுப்புகள் இருந்தால், மையமதிப்பை எளிதாகக் காணலாம். பொதுவாக ஒரு தரவுத்தொகுப்பில் ஒற்றை எண்ணிக்கையில் n உறுப்புகள் இருந்தால் , அதன் இடைநிலை அளவு (n +1 ) / 2  −ஆவது உறுப்பு ஆகும்.

(iv) ஒரு புள்ளி விவரத்தொகுப்பில் 6 உறுப்புகள் இருந்தால் எவ்வாறு இடைநிலை அளவு காண்பது? புள்ளி விவரத்தொகுப்பின் மையத்தில் உள்ள இரண்டு உறுப்புகளின் சராசரி இடைநிலை அளவு ஆகும் (3.5−வது உறுப்பு எனக் குறிப்பிடலாமா?).

ஒரு தரவுத்தொகுப்பில் 100 உறுப்புகள் இருந்தால் 50.5 -வது உறுப்பு இடைநிலை அளவு ஆகும்.

ஒரு தரவுத்தொகுப்பில் இரட்டை எண்ணிக்கையில் n உறுப்புகள் இருந்தால், அதன் இடைநிலை அளவு (n/2)  மற்றும் 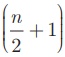( n/2 + 1 )  -ஆவது உறுப்புகளின் சராசரி ஆகும்.

ஏறு அல்லது இறங்கு வரிசையில் அமைக்கப்பட்ட தரவுகளை இரண்டு சம பாகங்களாகப் பிரிக்கும் மைய மதிப்பு இடைநிலை அளவு ஆகும். இது ஒரு நிலையான சராசரி (positional average) ஆகும்.

எடுத்துக்காட்டு 8.8

ஒரு மட்டைப் பந்தாட்டத்தில் 11 வீரர்கள் எடுத்த ஓட்டங்கள் முறையே 7, 21, 45, 12, 56, 35, 25, 0, 58, 66, 29 எனில், அவற்றின் இடைநிலை அளவு காண்க.

தீர்வு

கொடுக்கப்பட்ட எண்களை ஏறு வரிசையில் பின்வருமாறு எழுதுவோம்.

0, 7, 12, 21, 25, 29, 35, 45, 56, 58, 66

உறுப்புகளின் எண்ணிக்கை = 11 (ஓர் ஒற்றைப்படை எண்)

இடைநிலை அளவு = ( [11+1] / 2 ) ஆவது உறுப்பு

= ( 12/2 ) ஆவது உறுப்பு = 6 ஆவது உறுப்பு = 29

எடுத்துக்காட்டு 8.9

10,17,16,21,13,18,12,10,19,22, என்ற வகைப்படுத்தப்படாத தரவுகளின் இடைநிலை அளவு காண்க

தீர்வு

கொடுக்கப்பட்ட எண்களை ஏறு வரிசையில் பின்வருமாறு எழுதுவோம்: 10,10,12,13,16,17,18,19,21,22.

உறுப்புகளின் எண்ணிக்கை = 10 (ஓர் இரட்டைப்படை எண்)

இடைநிலை அளவு = (10/2) ஆவது உறுப்பு மற்றும் ( 10/ 2 + 1 ) ஆவது உறுப்புகளின் சராசரி

= 5 ஆவது உறுப்பு மற்றும் 6 ஆவது உறுப்புகளின் சராசரி

= (16 +17 ) / 2 = 33 / 2 = 16.5

எடுத்துக்காட்டு 8.10

கீழே கொடுக்கப்பட்டுள்ள அட்டவணையில், ஒரு வகுப்பில் கணிதம் மற்றும் அறிவியல் தேர்வினை எழுதிய 12 மாணவர்களின் மதிப்பெண்கள்.

எந்தப் பாடத்தில் மாணவர்கள் அதிக மதிப்பெண் பெற்றுள்ளனர்?

தீர்வு

மதிப்பெண்களை ஏறு வரிசையில் எழுதவும்.

மாணவர்களின் எண்ணிக்கை 12 எனவே 6 வது மற்றும் 7 வது மதிப்பெண் பெற்ற மாணவர்களின் மதிப்பெண் சராசரி இடைநிலை அளவு ஆகும்.

கணிதப் பாடத்தின் இடைநிலை அளவு = (44 + 50) / 2 = 47 

அறிவியல் பாடத்தின் இடைநிலை அளவு = (42 + 42) / 2 = 42

எனவே, கணிதப் பாடத்தின் மதிப்பெண் அறிவியல் பாடத்தைக் காட்டிலும் சிறந்தது என முடிவு செய்யலாம்.

1. இடைநிலை அளவு  − வகைப்படுத்தப்படாத நிகழ்வெண் பரவல் (Median −Ungrouped Frequency Distribution)

(i) கொடுக்கப்பட்ட எண்களை ஏறு அல்லது இறங்கு வரிசையில் எழுதவும்.

(ii) குவிவு நிகழ்வெண் பரவலைக் கணக்கிடவும். N மொத்த நிகழ்வெண்.

(iii) N −என்பது ஒரு ஒற்றைப்படை எண்ணாக இருந்தால், இடைநிலை அளவு = ( N+1 / 2 ) 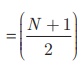 ஆவது உறுப்பு.

(iv) N −என்பது ஒரு இரட்டைப்படை எண்ணாக இருந்தால் இடைநிலை அளவு

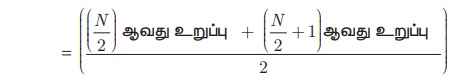
எடுத்துக்காட்டு 8.11

இடைநிலை அளவு காண்க

தீர்வு

கொடுக்கப்பட்ட தரவுகளை ஏறு வரிசையில் பின்வருமாறு எழுதுவோம்.

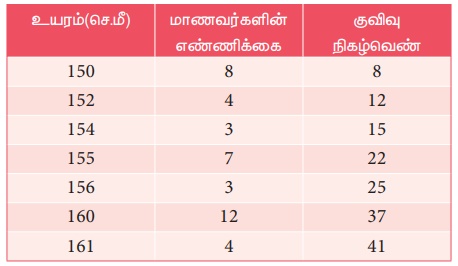
இங்கு N = 41

இடைநிலை அளவு = ( N+1 / 2 ) 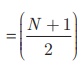 ஆவது மதிப்பு = ( [41+1] / 2 ) ஆவது மதிப்பு = 21 ஆவது மதிப்பு.

41 மாணவர்களின் உயரங்களை ஏறுவரிசையில் வரிசைப்படுத்தினால் 21ஆவது மாணவரின் உயரம் மைய மதிப்பாக இருக்கும். இவரின் இருபுறமும் 20 பேர் உள்ளனர். எனவே நாம் 21ஆவது மாணவரின் உயரத்தைக் காண்பது அவசியமாகிறது. 15 மாணவர்கள் (குவிவு நிகழ்வெண் பார்க்கவும்) 154 செ.மீ உயரத்திற்குச் சமமாகவோ அல்லது குறைவாகவோ உள்ளனர். 22 மாணவர்கள் (குவிவு நிகழ்வெண் பார்க்கவும்) 155 செ.மீ உயரத்திற்குச் சமமாகவோ அல்லது உயரமாகவோ உள்ளனர். இதிலிருந்து 21ஆவது மாணவரின் உயரம் 155 செ.மீ என்பதை அறியலாம்.

இடைநிலை அளவு = 155 செ.மீ

2. இடைநிலை அளவு  − வகைப்படுத்தப்பட்ட நிகழ்வெண் பரவல் (Median  − Grouped Frequency Distribution)

வகைப்படுத்தப்பட்ட நிகழ்வெண் பரவலின் இடைநிலை அளவின் கணக்கீடு கீழ்க்காணும் படிகளைக் கொண்டது.

படிகள்

(i) குவிவு நிகழ்வெண் பரவலைக் கணக்கிடவும்.

(ii) N என்பது நிகழ்வெண்களின் கூடுதல் எனில், N/2 இன் மதிப்பைக் காண்க

(iii) குவிவு நிகழ்வெண் N/2 ஐ உறுப்பாகக் கொண்டிருக்கும் பிரிவு இடைவெளி, இடைநிலை அளவு பிரிவு என்று அழைக்கப்படும்.

(iv) இடைநிலை அளவு = 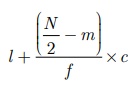என்ற வாய்ப்பாட்டைப் பயன்படுத்திக் காணலாம்.

இங்கு l = இடைநிலை அளவு பிரிவின் கீழ் எல்லை

f = இடைநிலை அளவு பிரிவின் நிகழ்வெண்

c = இடைநிலை அளவு பிரிவின் நீளம்

N = நிகழ்வெண்களின் கூடுதல் (∑f)

 m = இடைநிலை அளவுப் பிரிவின் குவிவு நிகழ்வெண்ணுக்கு உடனடியான முந்தைய குவிவு நிகழ்வெண்

முன்னேற்றத்தைச் சோதித்தல்

1. முதல் நான்கு முழு எண்களின்இடைநிலை அளவு ……………

2. முதல் நான்கு முழு எண்களுடன் நான்கு என்ற எண்ணைச் சேர்க்கும் போது இடைநிலை அளவு காண்க.

3. இரு இடைநிலை அளவுகளுக்கிடையே உள்ள வேறுபாடு …………….._

எடுத்துக்காட்டு 8.12

கொடுக்கப்பட்டுள்ள 200 குடும்பங்களின் வாராந்திரச் செலவுக் குறிப்புகளின் இடைநிலை அளவு காண்க.

தீர்வு

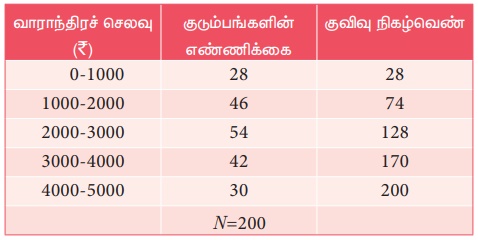
N=200

இடைநிலை அளவு = ( N / 2 ) ஆவது மதிப்பு = ( 200 / 2 ) ஆவது மதிப்பு

= 100 ஆவது மதிப்பு

இடைநிலைப் பிரிவு = 2000  − 3000

N / 2   = 100 ,  l = 2000

m = 74, c = 1000,  f = 54

இடைநிலை அளவு =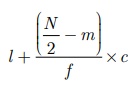

= 2000 + [(100 – 74) / 54  ] × 1000

= 2000 + (26/54)  × 1000 = 2000 + 481.5

= 2481.5

எடுத்துக்காட்டு 8.13

கீழ்க்காணும் தரவுகளின் இடைநிலை அளவு 24 எனில் x இன் மதிப்பைக் காண்க.

தீர்வு

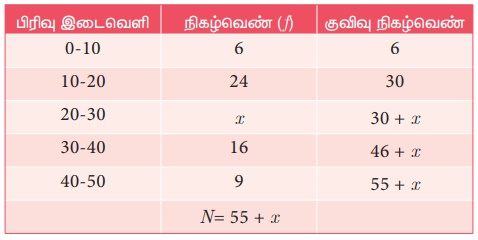
இடைநிலை அளவு 24 எனில் இடைநிலைப் பிரிவு 20 – 30

l = 20,   N = 55 + x,  m = 30,  c = 10,   f = x

இடைநிலை அளவு =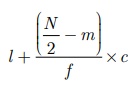 

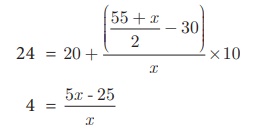
(எளிமையாக்கிய பிறகு)

4 = (5x – 25 ) / x  

4x = 5x – 25

5x  − 4x = 25

x = 25