அட்டவணை, எடுத்துக்காட்டு, தீர்வுகள் | புள்ளியியல் | கணக்கு - முகடு | 9th Maths : UNIT 8 : Statistics
9 ஆம் வகுப்பு கணக்கு : அலகு 8 : புள்ளியியல்
முகடு
முகடு
மூன்று வேட்பாளர்கள் பெற்ற வாக்குகள் பற்றிய தரவுகள் கீழே கொடுக்கப்பட்டுள்ளன:
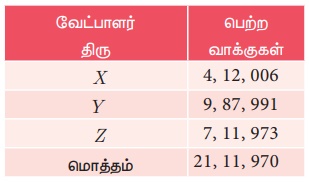
எந்த வேட்பாளர் வெற்றி பெற்றவராக அறிவிக்கப்படுவார்?
கண்டிப்பாக மிக அதிக எண்ணிக்கையிலான வாக்குகளைப் பெற்ற திரு.Y அவர்கள்தான். ஆனால் அவருக்கு எதிரான வாக்குகளின் மொத்த எண்ணிக்கை அதிகம். ஆனாலும் இங்கு அவர்தான் வெற்றி பெற்ற வேட்பாளராகிறார். ஏனெனில் இங்கு தேர்வு என்பது போட்டியாளர்களில் யார் அதிக வாக்குகள் பெற்றவர் என்பதைப் பொருத்து அமைகிறது.

ஒரு நிறுவனம் ஒரு பள்ளியின் 9 ஆம் வகுப்பில் உள்ள 100 மாணவர்களுக்கு விளையாட்டுக் காலணிகளை அளிக்க விரும்புகிறது. அந்த வகுப்பில் உள்ள மாணவர்களின் காலணிகளின் அளவுகள் கீழே கொடுக்கப்பட்டுள்ளன.

அந்த நிறுவனம் எந்த அளவுடைய காலணிகளை அதிக எண்ணிக்கையில் வாங்க வேண்டும்?
மேற்கண்ட இரண்டு எடுத்துக்காட்டுகளிலிருந்து
சராசரி மற்றும் இடைநிலை அளவு காண்பது இந்தச் சூழ்நிலைக்குப் பொருத்தமற்றதாக இருக்கும் என்று அறியலாம். இதுபோன்ற நிகழ்வில் நமக்கு வேறு வகையான ஒரு சராசரி தேவைப்படுகிறது. அதன் பெயர் முகடு ஆகும்.
அதிகமுறை இடம் பெற்றுள்ள உறுப்பின் மதிப்பே முகடு ஆகும்.
சராசரியைப் பற்றிய காணொலிகளை வலையொளித் தளத்தில் தேடும்போது அதிகமாகப் பார்க்கப்பட்ட ஒரு காணொலியைப் பார்க்க நேரிடும். இந்த இடத்தில் முகடு என்ற கருத்து பயன்படுத்தப்படுகிறது.
1. முகடு − செப்பனிடப்படாதத் தரவு (Mode − Raw Data)
அதிக முறை இடம் பெற்றுள்ள உறுப்பின் மதிப்பே முகடு ஆகும்.
எடுத்துக்காட்டு 8.14
ஓர் அரிசி ஆலையில் உள்ள ஏழு தொழிலாளிகளின் நாள்கூலித் தரவுகள் முறையே ₹ 500, ₹ 600, ₹ 600, ₹
800, ₹ 800, ₹ 800 மற்றும்
₹ 1000. நாள்கூலித்
தரவுகளின் முகடு காண்க.
தீர்வு
இத்தரவில் ₹ 800 அதிகமான(மூன்று) முறை இடம் பெற்று, மற்றவை இரண்டு அல்லது ஒருமுறை இடம்பெற்றிருப்பதால்,
முகடு ₹ 800 ஆகும்.
எடுத்துக்காட்டு 8.15
பின்வரும் எண்களுக்கு முகடு காண்க 17, 18, 20, 20, 21,
21, 22, 22
தீர்வு
இத்தரவில் 20, 21, 22 என்ற எண்கள் ஒவ்வொன்றும் இருமுறை இடம்பெறுவதால், இத்தரவுகளுக்கு 20, 21, 22 ஆகிய மூன்று முகடுகள் உள்ளன.
குறிப்பு
• ஒரே ஒரு முகடு உள்ள பரவல் ஒற்றை முகட்டுப் பரவல் எனப்படும்.
• இரண்டு முகடுகள் உள்ள பரவல் இரட்டை முகட்டுப் பரவல் எனப்படும்.
• மூன்று முகடுகள் உள்ள பரவல் மும்முகட்டுப் பரவல் எனப்படும்.
• மூன்று முகடுகளுக்கு மேல் உள்ள பரவல் பன்முகட்டுப் பரவல் எனப்படும்.
2. முகடு − வகைப்படுத்தப்படாத நிகழ்வெண் பரவல் (Mode for
Ungrouped Frequency Distribution)
வகைப்படுத்தப்படாத நிகழ்வெண் பரவலில் மிகப்பெரிய நிகழ்வெண்ணைப் பெற்றுள்ள உறுப்பின் மதிப்பு முகடு எனப்படும்.
எடுத்துக்காட்டு 8.16
ஓர் எண் தொகுப்பானது ஐந்து 4 களையும், நான்கு 5 களையும், ஒன்பது 6 களையும், ஆறு 9 களையும் கொண்டுள்ளது. எனில் முகடு காண்க.
தீர்வு

கொடுக்கப்பட்ட தரவில், மிகப்பெரிய நிகழ்வெண் 9 ஐப் பெற்றிருக்கும் அளவு 6. எனவே முகடு 6 ஆகும்.
3. முகடு−வகைப்படுத்தப்பட்ட நிகழ்வெண் பரவல் (Mode−Grouped Frequency Distribution)
வகைப்படுத்தப்பட்ட நிகழ்வெண் பரவலில், உறுப்புகளின் சரியான மதிப்பு தெரியாது என்பதால் முகட்டின் சரியான மதிப்பைக் காண்பது மிகக் கடினமானது. எனினும், பிரிவு இடைவெளிகளின் நீளம் சமமானதாக உள்ள போது முகட்டின் தோராய மதிப்பைக் கீழ்வரும் வாய்ப்பாட்டின் மூலம் காணலாம்.
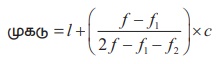
இங்கு மிகப்பெரிய நிகழ்வெண்ணைப் பெற்றுள்ள பிரிவை முகட்டுப் பிரிவு என்று அழைப்போம்.
l − முகட்டுப்
பிரிவின் கீழ் எல்லை
f − முகட்டுப்
பிரிவின் நிகழ்வெண்
f1
− முகட்டுப் பிரிவின் நிகழ்வெண்ணுக்கு முந்தைய நிகழ்வெண்
f2
− முகட்டுப் பிரிவின் நிகழ்வெண்ணுக்குப் பிந்தைய நிகழ்வெண்
எடுத்துக்காட்டு 8.17
கீழ்க்காணும் தரவுகளுக்கு முகடு காண்க.

தீர்வு
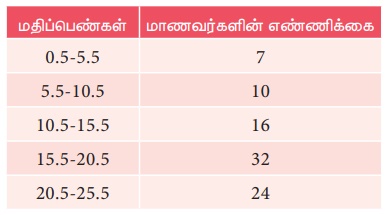
முகட்டுப் பிரிவு 16−20 (ஏனெனில் இப்பிரிவு மிகப்பெரிய நிகழ்வெண்ணை பெற்றிருக்கிறது.).
l
= 15.5, f = 32, f1 = 16, f2 =24, c =
20.5 −15.5 = 5
முகடு = 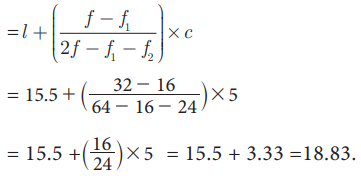
= 15.5 + [ ( 32 – 16) / ( 64 – 16 – 24 ) ] × 5
= 15.5 + ( 16 / 24 )
×
5 = 15.5 + 3. 33 = 18.83.
குறிப்பு
தொடர்ச்சியில்லாத பிரிவு இடைவெளியைத் தொடர்ச்சியான பிரிவு இடைவெளியாக மாற்றுவதற்கு ஒவ்வொரு இடைவெளியின் கீழ் எல்லையிலிருந்து 0.5 ஐக் கழிக்க வேண்டும் மற்றும் மேல் எல்லையுடன் 0.5ஐக் கூட்ட வேண்டும்.
4. சராசரி , இடைநிலை அளவு, முகடு இவற்றிலிருந்து பெறப்பட்ட உறவு (An Empirical Relationship Between Mean, Median and Mode).
நிகழ்வெண்கள் சீராகப் பரவி இருக்கும்போது ஏற்கனவே அறிந்த மூன்று வகையான சராசரிகளுக்கும் இடையே ஒருவகைத் தொடர்பு ஏற்படும்.
முகடு ≅ 3
இடைநிலை அளவு − 2 சராசரி
எடுத்துக்காட்டு 8.18
ஒரு பரவலின் சராசரி மற்றும் முகடு முறையே 66 மற்றும் 60 ஆகும். இடைநிலை அளவு காண்க.
தீர்வு
சராசரி = 66 முகடு
= 60
முகடு ≅ 3 இடைநிலை அளவு − 2 சராசரி
60 ≅ 3 இடைநிலை அளவு – 2(66)
3 இடைநிலை
அளவு ≅ 60 + 132
இடைநிலை அளவு ≅ 192 / 3 ≅ 64