வரையறை, பொது வடிவம், தேற்றம், விளக்க எடுத்துக்காட்டு - அணிகள்(Matrices) | 11th Mathematics : UNIT 7 : Matrices and Determinants
11 வது கணக்கு : அலகு 7 : அணிகளும் அணிக்கோவைகளும் (Matrices and Determinants)
அணிகள்(Matrices)
அணிகள்(Matrices)
உறுப்புகள் அல்லது மூலகங்களை செவ்வக வடிவில் நிரைகள் மற்றும் நிரல்களாக [ ] என்ற அடைப்புக்குறியினுள் குறிப்பிடுவது அணியாகும்.
ஓர் அணியின் உறுப்புகள் பொதுவாக மெய்யெண்கள், கலப்பெண்கள், ஒருமாறிச் சார்புகள், (அதாவது பல்லுறுப்புக் கோவைகள், முக்கோணவியல் சார்புகள் மற்றும் இவற்றின் கலப்பாக) பலமாறிச் சார்புகள் உறுப்பாக இருக்கலாம். அணிகளை A, B, C, ....... என்ற எழுத்துக்களால் குறிப்பிடுவது வழக்கம். இப்பாடப்பகுதியில் மெய்யெண்கள் அல்லது மெய் மதிப்புடையச் சார்புகளை மட்டுமே அணியின் உறுப்புகளாக எடுத்துக் கொள்வோம்.
அணியின் பொது வடிவம் (General form of a matrix)
m நிரைகள் (rows) மற்றும் n நிரல்கள் (columns) கொண்ட ஓர் அணி A−யினை பின்வருமாறு எழுதலாம்.
A =[aij]m×n , 1 ≤ i ≤ m , 1 ≤ j ≤ n. அதாவது

இங்கு m, n என்பன மிகை முழு எண்களாகும்.
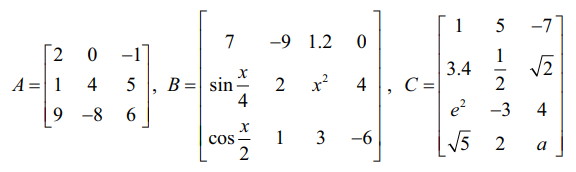
ஆகியவை அணிகளுக்கான சில உதாரணங்கள் ஆகும்.
ஓர் அணியில், உறுப்புகளின் கிடைமட்ட வரிசைகள் நிரைகள் எனவும், செங்குத்து வரிசைகள் நிரல்கள் எனவும் அழைக்கப்படுகின்றன. எனவே, அணி A ஆனது 3 நிரைகள் மற்றும் 3 நிரல்களையும், B என்பது 3 நிரைகள் மற்றும் 4 நிரல்களையும், C என்பது 4 நிரைகள் மற்றும் 3 நிரல்களையும் கொண்டுள்ளன.
வரையறை 7.1
ஓர் அணி A ஆனது m நிரைகள் மற்றும் n நிரல்களைப் பெற்றிருந்தால் m×n (m by n எனப்படிக்கவும்) என்பது அந்த அணியின் வரிசை அல்லது பரிமாணம் எனப்படும்.
a11, a12, .... amn என்பன A = [aij]m×n என்ற அணியின் உறுப்புகள் அல்லது மூலகங்கள் எனப்படும். i −ஆவது நிரை மற்றும் j− ஆவது நிரலில் உள்ள பொது உறுப்பு aij ஆகும். இவ்வுறுப்பு அணி A−ன் (i , j)− ஆவது உறுப்பு எனப்படும். அணி A−ன் i−ஆவது நிரை மற்றும் j −ஆவது நிரல் ஆகியவை முறையே 1 × n மற்றும் m × 1 வரிசை உடைய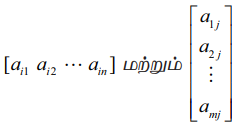 என்ற அணிகளாகும்.
என்ற அணிகளாகும்.
நடைமுறை வாழ்க்கைக் கணக்குகளை அணி அமைப்பில் எழுதி அவற்றின் தீர்வுகளை எவ்வாறு காண்பது எனக் காண்போம்.
விளக்க எடுத்துக்காட்டு 7.1
எடுத்துக்காட்டாக பல்வேறு தேர்வுகளில் பல்வேறு பாடப்பிரிவுகளில் ஒரு மாணவர் பெற்ற மதிப்பெண்களைப் பின்வருமாறு அட்டவணைப்படுத்துவோம்.

இந்த அட்டவணையில் உள்ள விவரங்களை அணி வடிவத்திற்கு மாற்றலாம். அட்டவணையில் உள்ள மதிப்பெண்களை 3 × 5 வரிசை கொண்ட அணி அமைப்பில் பின்வருமாறு எழுதலாம். இதில் மூன்றாவது நிரை மற்றும் இரண்டாவது நிரலில் உள்ள உறுப்பு எதனைக் குறிக்கின்றது?
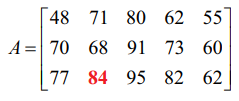
மேற்கண்ட அணியில் மூன்றாவது நிரை மற்றும் இரண்டாவது நிரலில் அமைந்துள்ள 84 என்ற உறுப்பு, ஆங்கிலப் பாடப்பிரிவில் தேர்வு 3−ல் அம்மாணவர் பெற்ற மதிப்பெண்ணைக் குறிப்பிடுகிறது.
எடுத்துக்காட்டு 7.1
ஓர் அணியில் 12 உறுப்புகள் உள்ளது. அவ்வணியின் வாய்ப்புள்ள வரிசைகளைக் காண்க. மேலும், அந்த அணியில் 7 உறுப்புகள் இருந்தால் வரிசைகள் என்னவாகும்?
தீர்வு
ஓர் அணியின் நிரைகளின் எண்ணிக்கை மற்றும் நிரல்களின் எண்ணிக்கை ஆகியவற்றைப் பெருக்கினால் அவ்வணியில் உள்ள உறுப்புகளின் எண்ணிக்கை கிடைக்கும். எனவே, இரு இயல் எண்களின் பெருக்கற் பலன் 12 தரக்கூடிய எல்லா வரிசை ஜோடிகளையும் காணலாம். ஆகவே, பெருக்கற்பலன் 12 தரக்கூடிய 12−ன் இரண்டு வகு எண்களைக் கொண்டு பெறக்கூடிய பெருக்கல்களான 1 × 12, 12 × 1, 2 × 6, 6 × 2, 3 × 4 மற்றும் 4 × 3 ஆகியவை வரிசைகளாக அமையலாம்.
மேலும் ஓர் அணியில் 7 உறுப்புகள் இருந்தால், 7 என்பது பகா எண் என்பதால் 1 × 7 மற்றும் 7 × 1 என்பவை மட்டுமே அணியின் வரிசைகளாக அமையும்.
எடுத்துக்காட்டு 7.2
aij = √3/2 |2i − 3j|, (1 ≤ i ≤ 2, 1 ≤ j ≤ 3) என இருக்குமாறு (i, j) −ஆவது உறுப்புகளைக் கொண்ட 2 × 3 அணியை எழுதுக.
தீர்வு
2 × 3 அணியின் பொது வடிவம் 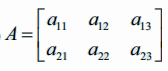
aij −ன் வரையறையின்படி, 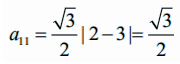 இதே போன்று A என்ற அணியின் மற்ற உறுப்புகளையும் காணலாம். எனவே தேவையான அணி
இதே போன்று A என்ற அணியின் மற்ற உறுப்புகளையும் காணலாம். எனவே தேவையான அணி 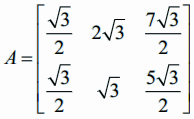
1. அணிகளின் வகைகள் (Types of matrices)
நிரை, நிரல், பூஜ்ஜிய அணிகள் (Row, Column, Zero matrices)
வரையறை 7.2
ஒரே ஒரு நிரையை மட்டுமே உடைய அணி நிரை அணி எனப்படும்.
எடுத்துக்காட்டாக,
A = [A]1×4 = [1 0 − 1.1 √2] என்பது 1× n வரிசை உடைய நிரை அணியாகும்.
A = [aij]1×n = [aij]1×n என்பது 1×n வரிசை உடைய நிரை அணியின் பொது அமைப்பாகும்.
வரையறை 7.3
ஒரே ஒரு நிரலை மட்டுமே உடைய அணி நிரல் அணி எனப்படும்.
எடுத்துக்காட்டாக, [A]4×1 = 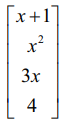 என்பது m×1 வரிசை உடைய நிரல் அணியாகும். இதன் உறுப்புகள் மெய்யெண் சார்புகள் ஆகும். A = [aij]m×1 = [ai1]m×1 என்பது m×1 வரிசை உடைய நிரல் அணியின் பொது வடிவமாகும்.
என்பது m×1 வரிசை உடைய நிரல் அணியாகும். இதன் உறுப்புகள் மெய்யெண் சார்புகள் ஆகும். A = [aij]m×1 = [ai1]m×1 என்பது m×1 வரிசை உடைய நிரல் அணியின் பொது வடிவமாகும்.
வரையறை 7.4
ஓர் அணி A = [aij]m×n −இல் அனைத்து 1 ≤ i ≤ m மற்றும் 1 ≤ j ≤ n மதிப்புகளுக்கும் aij = 0 எனில், இவ்வணி பூஜ்ஜிய அணி எனப்படும். இது O எனக்குறிக்கப்படும்.
எடுத்துக்காட்டாக, [0], 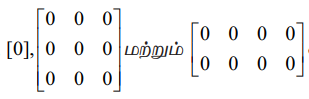 என்பன முறையே 1×1, 3×3, மற்றும் 2 × 4 வரிசை உடைய பூஜ்ஜிய அணிகளாகும்.
என்பன முறையே 1×1, 3×3, மற்றும் 2 × 4 வரிசை உடைய பூஜ்ஜிய அணிகளாகும்.
ஓர் அணி A−ல் குறைந்தபட்சம் ஓர் உறுப்பு பூஜ்ஜியமற்றது எனில், அவ்வணி பூஜ்ஜியமற்ற அணி எனப்படும்.
சதுர, மூலைவிட்ட, அலகு மற்றும் முக்கோண வடிவ அணிகள் (Square, Diagonal, Unit, Triangular matrices)
வரையறை 7.5
ஓர் அணியின் நிரை மற்றும் நிரல்களின் எண்ணிக்கை சமம் எனில், அவ்வணி சதுர அணி எனப்படும். அதாவது, n × n வரிசை உடைய ஒரு சதுர அணி n வரிசை உடைய சதுர அணி எனப்படும்.
எடுத்துக்காட்டாக, 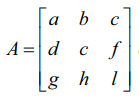 என்பது 3 வரிசையுடைய ஒரு சதுர அணியாகும்.
என்பது 3 வரிசையுடைய ஒரு சதுர அணியாகும்.
வரையறை 7.6
n வரிசை உடைய ஒரு சதுர அணி A= [aij]m×n −ன் உறுப்புகள் a11, a22, a33,… ,amn என்பன முதன்மை மூலைவிட்ட அல்லது பிரதான மூலைவிட்ட உறுப்புகள் எனப்படும்.
வரையறை 7.7
A = [aij]m×n என்ற சதுர அணியில் அனைத்து aij = 0, i # j எனில், அவ்வணி ஒரு மூலைவிட்ட அணி எனப்படும்.
எனவே, ஒரு மூலைவிட்ட அணியில் பிரதான மூலைவிட்ட உறுப்புகளைத் தவிர மற்ற அனைத்து உறுப்புகளும் பூஜ்ஜியமாகும். எடுத்துக்காட்டாக,
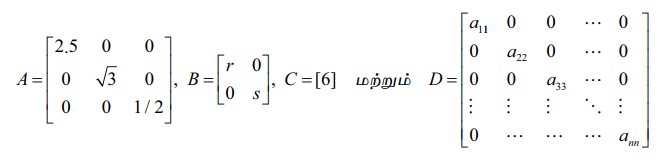
என்பன முறையே 3, 2, 1 மற்றும் n வரிசை உடைய மூலைவிட்ட அணிகளாகும். ஒரு பூஜ்ஜிய சதுர அணி ஒரு மூலைவிட்ட அணியாகுமா?
வரையறை 7.8
ஒரு மூலைவிட்ட அணியில் முதன்மை மூலைவிட்ட உறுப்புகள் அனைத்தும் சமம் எனில், அவ்வணி ஒரு திசையிலி அணி எனப்படும்.
A = [aij]m×n என்ற சதுர அணியில் aij = 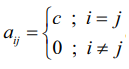 எனில்,
எனில்,
A என்ற அணி திசையிலி அணியாகும். இங்கு c என்பது ஒரு நிலை எண்ணாகும்.
எடுத்துக்காட்டாக,
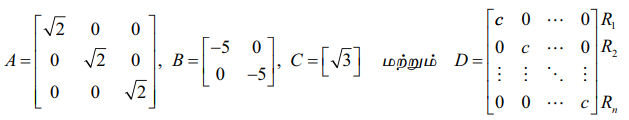
என்பன முறையே வரிசை 3, 2, 1 மற்றும் n உடைய திசையிலி அணிகளாகும்.
மேலும், ஒரு பூஜ்ஜிய சதுர அணி, திசையிலி 0 உடைய திசையிலி அணியாகும் என்பதை கவனத்தில் கொள்க.
வரையறை 7.9
ஒரு சதுர அணியில் முதன்மை மூலைவிட்ட உறுப்புகள் அனைத்தும் 1 ஆகவும் மற்ற உறுப்புகள் அனைத்தும் பூஜ்ஜியமாகவும் இருந்தால், அவ்வணி அலகு அணி அல்லது சமனி அணி எனப்படும். எனவே,
A = [aij]m×n என்ற சதுர அணியில் 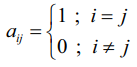 எனில், A என்பது ஓர் அலகு அணியாகும்.
எனில், A என்பது ஓர் அலகு அணியாகும்.
மேலும், n வரிசை உடைய அலகு அணியை In எனக் குறிக்கிறோம்.
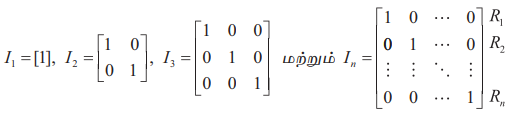
என்பன முறையே வரிசை 1, 2, 3 மற்றும் n உடைய அலகு அணிகளுக்கான எடுத்துக்காட்டுகளாகும்.
குறிப்பு 7.1
அலகு அணியானது ஒரு திசையிலி அணிக்கு எடுத்துக்காட்டாகும்.
முக்கோண வடிவ அணிகளில், மேல் முக்கோண வடிவ அணி மற்றும் கீழ் முக்கோண வடிவ அணி என இரண்டு வகைகள் உள்ளன.
வரையறை 7.10
ஒரு சதுர அணியில் முதன்மை மூலைவிட்டத்திற்குக் கீழ் உள்ள அனைத்து உறுப்புகளும் பூஜ்ஜியம் எனில் அவ்வணி மேல் முக்கோண வடிவ அணி எனப்படும்.
எனவே A = [aij]m×n என்ற சதுர அணியில் aij = 0, i > j எனில், அவ்வணி மேல் முக்கோண வடிவ அணியாகும்.
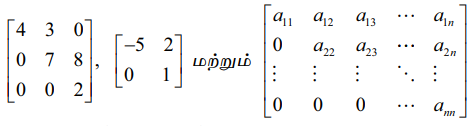 என்பன மேல் முக்கோண வடிவ அணிகளுக்கான எடுத்துக்காட்டுகளாகும்.
என்பன மேல் முக்கோண வடிவ அணிகளுக்கான எடுத்துக்காட்டுகளாகும்.
வரையறை 7.11
ஒரு சதுர அணியில் முதன்மை மூலைவிட்டத்திற்கு மேல் உள்ள அனைத்து உறுப்புகளும் பூஜ்ஜியம் எனில், அவ்வணி கீழ் முக்கோண வடிவ அணி எனப்படும்.
எனவே, A = [aij]m×n என்ற சதுர அணியில் aij = 0, i < j எனில், அவ்வணி கீழ் முக்கோண வடிவ அணியாகும்.
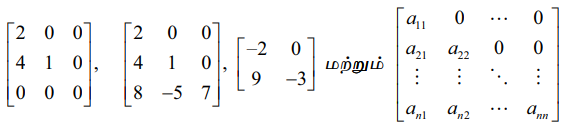 என்பன கீழ் முக்கோண வடிவ அணிகளுக்கு எடுத்துக்காட்டுகளாகும்.
என்பன கீழ் முக்கோண வடிவ அணிகளுக்கு எடுத்துக்காட்டுகளாகும்.
வரையறை 7.12
மேல் முக்கோண வடிவில் அல்லது கீழ் முக்கோண வடிவில் உள்ள ஒரு சதுர அணியை முக்கோண வடிவ அணி என்கிறோம்.
மேலும், ஒரே நேரத்தில் மேல் மற்றும் கீழ் முக்கோண வடிவில் உள்ள ஒரு சதுர அணியானது ஒரு மூலைவிட்ட அணியாக அமைவதைக் காணலாம்.
2. அணிகளின் சமத்தன்மை (Equality of Matrices)
வரையறை 7.13
A = [aij] மற்றும் B = [bij] என்ற இரு அணிகள் சம அணிகள் (A = B எனக் குறிப்பிடுவோம்) எனில்
(i) A, B என்ற அணிகள் ஒரே வரிசை அல்லது பரிமாணம் உடையவையாகும்.
(ii) A, B ஆகிய அணிகளின் ஒத்த உறுப்புகள் சமமாக இருக்கும். அதாவது, அனைத்து i, j −க்கு aij = bij ஆக இருக்கும். இதன் மறுதலையும் உண்மையாகும்.
எடுத்துக்காட்டாக,
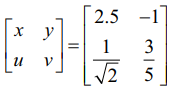 எனில், x = 2.5, y = −1, u = 1/√2 மற்றும் v = 3/5 எனப்பெறுகிறோம்.
எனில், x = 2.5, y = −1, u = 1/√2 மற்றும் v = 3/5 எனப்பெறுகிறோம்.
வரையறை 7.14
A, B என்ற இரு அணிகளுக்கு வரையறை 7.13−ல் உள்ள நிபந்தனைகள் (i) அல்லது (ii) இவற்றில் ஏதேனும் ஒன்று பூர்த்தி செய்யப்படவில்லை என்றால், அவ்விரு அணிகளும் சமமற்றவை எனப்படும்.
எடுத்துக்காட்டாக, 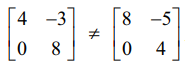 ஏனெனில் இவ்வணிகளின் ஒத்த உறுப்புகள் சமமற்றவை.
ஏனெனில் இவ்வணிகளின் ஒத்த உறுப்புகள் சமமற்றவை.
மேலும் 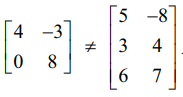 ஏனெனில் இவ்வணிகளின் வரிசைகள் சமமல்ல.
ஏனெனில் இவ்வணிகளின் வரிசைகள் சமமல்ல.
எடுத்துக்காட்டு 7.3
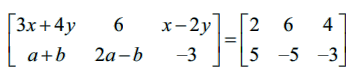 எனில், x, y, a, b இவற்றின் மதிப்புகளைக் காண்க.
எனில், x, y, a, b இவற்றின் மதிப்புகளைக் காண்க.
தீர்வு
இரண்டு அணிகளும் சம அணிகள் என்பதால், அவற்றின் ஒத்த உறுப்புகளும் சமம். எனவே, 3 x + 4y =2, x − 2y = 4, a + b = 5, 2 a – b = −5
இச்சமன்பாடுகளின் தீர்வு காண, x = 2, y = −1, a = 0, b = 5 எனக் கிடைக்கும்.
3. அணிகளின் மீதான இயற்கணிதச் செயல்முறைகள் (Algebraic Operations on Matrices)
இப்பகுதியில் அணிகளின் அடிப்படைச் செயல்களான
(1) ஓர் அணியை திசையிலியால் பெருக்குதல்
(2) அணிகளின் கூட்டல் மற்றும் கழித்தல்
(3) அணிகளின் பெருக்கல்
ஆகியவற்றைப் பார்ப்போம்.
ஓர் அணியை மற்றோர் அணியால் வகுத்தல் பற்றிய கருத்தாக்கம் வரையறுக்கப்படவில்லை. எனவே, A, B என்ற ஏதேனும் இரண்டு அணிகளுக்கு A/B என்ற செயல்பாடு வரையறுக்கப்படவில்லை.
(1) ஓர் அணியைத் திசையிலியால் பெருக்குதல்
ஓர் அணி A = [aij]m×n மற்றும் k என்பது மெய் திசையிலி என்க. இப்போது, kA = [bij]m×n என்ற புதிய அணியை வரையறுப்போம். இங்கு, அனைத்து i, j−க்கு bij = kaij ஆகும்.
எடுத்துக்காட்டாக, A = 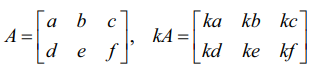
குறிப்பாக, k = −1 எனில், −A=[−aij]m×n எனப்பெறுகிறோம். இந்த − A என்பது A என்ற அணியின் எதிர்மறை அணி எனப்படும்.
(2) இரண்டு அணிகளின் கூட்டல் மற்றும் கழித்தல்
A, B என்பவை ஒரே வரிசையுடைய இரு அணிகள் எனில் இவற்றின் கூடுதல் அதே வரிசையுள்ள அணியாகும். இவ்வணி A + B எனக் குறிக்கப்பட்டு A, B−ன் ஒத்த உறுப்புகளைக் கூட்டுவதன் மூலம் பெறப்படுகிறது.
A = [aij]m×n , B = [bij]m×n என்ற இரு அணிகளின் கூடுதல் A + B = [cij]m×n என்ற அணியாகும். இங்கு அனைத்து i, j−க்கு cij = aij + bij ஆகும்.
இதேபோல், கழித்தல் A − B ஆனது A − B = A + (−1)B என வரையறுக்கப்படுகிறது
அதாவது, A – B = [dij]m×n , இங்கு dij = aij − bij , ∀ i மற்றும் j.
(∀ என்ற குறியீடு ஒவ்வொரு அல்லது அனைத்து எனப் பொருள்படும்).
குறிப்பு 7.2
A, B என்ற அணிகளின் வரிசைகள் சமமற்றவை எனில், A + B மற்றும் A − B என்பவற்றை வரையறுக்க இயலாது.
அணிகளின் கூட்டல் மற்றும் கழித்தல் செயல்களை எந்த ஒரு முடிவுறு எண்ணிகையுள்ள அணிகளுக்கும் விரிவுபடுத்தலாம்.
எடுத்துக்காட்டு 7.4
 எனில், A + B மற்றும் A – B ஆகியவற்றைக் காண்க.
எனில், A + B மற்றும் A – B ஆகியவற்றைக் காண்க.
தீர்வு
அணிகளின் கூட்டல் மற்றும் கழித்தல் வரையறைகளின்படி,

எடுத்துக்காட்டு 7.5

(3) அணிகளின் பெருக்கல்
வரையறை 7.15
A என்ற அணியின் நிரல்களின் எண்ணிக்கையும் B என்ற அணியின் நிரல்களின் எண்ணிக்கையும் சமமாக இருப்பின் A என்ற அணி B என்ற அணியுடன் பெருக்கலுக்கு உகந்தது எனப்படும்.
அதாவது, A = [aij]m×n மற்றும் B = [bij]n×p என்பன இரு அணிகள் எனில், இவ்வணிகளின் பெருக்கல் AB எனக்குறிப்பிடப்படும். மேலும் இதன் வரிசை m × p ஆகும்.

எடுத்துக்காட்டு 7.8

குறிப்பு 7.3
(1) A = [aij]m×n , B = [bij]n×p, மற்றும் m ≠ p, எனில் AB என்ற பெருக்கல் அணியை வரையறுக்க முடியும். ஆனால் BA−ஐ காண முடியாது.
(2) மெய்யெண்களின் பின்வரும் அடிப்படைப் பண்புகள் அணிகளிலும் விவாதிக்கப்படுகிறது.
அதாவது,
ab = ba ∀a, b ∈ ℝ
ab = ac ⇒ b = c ∀ a,b,c ∈ ℝ , a ≠ 0
ab = 0 ⇒ a = 0 அல்லது b = 0 ∀ a,b ∈ ℝ
இதேப்போன்று அணிகளிலும் விவாதிக்கலாம். அதாவது,
(i) AB மற்றும் BA என்பவை வரையறுக்கப்பட்டிருந்தாலும், AB = BA ஆக இருக்கவேண்டிய அவசியமில்லை.
எடுத்துக்காட்டாக,
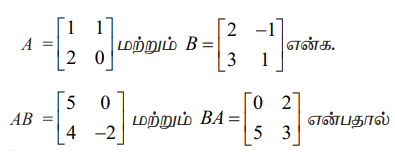
AB ≠ BA, எனக் காண்கிறோம்.
இந்நிலையில், A, B என்ற அணிகள் பெருக்கலைப் பொறுத்து பரிமாற்றுப் பண்பை பெறவில்லை என்கிறோம்.
மேலும் AB = BA என்பதும் சில நேரங்களில் உண்மையாகும். எடுத்துக்காட்டாக,
 எனக் காண்கிறோம்.
எனக் காண்கிறோம்.
(ii) அணிப்பெருக்கலில் நீக்கல் பண்பு உண்மையாகாது. அதாவது, n × n, n > 1 என்ற வரிசை உடைய A ≠ 0, B, C என்ற மூன்று சதுர அணிகளுக்கு, AB = AC எனில், B = C, மற்றும் BA = CA எனில், B = C என்பவை உண்மையாக இருக்கவேண்டிய அவசியமில்லை.
இவ்வுண்மைகளை, பின்வரும் எளிய எடுத்துக்காட்டின் மூலம் காணலாம்.
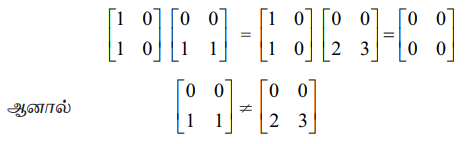
(iii) A ≠ 0 மற்றும் B ≠ 0 ஆக இருந்து AB = 0 ஆக வாய்ப்புள்ளது. அதாவது, AB = 0 எனில், A = 0 அல்லது B = 0 ஆக இருக்க வேண்டிய அவசியமில்லை. எடுத்துக்காட்டாக,
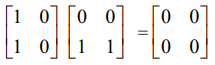
(3) கீழே கொடுக்கப்பட்டுள்ள அணிகளின் கூட்டல் மற்றும் பெருக்கல் செயல்களுக்கு உகந்த ஏதேனும் இரு அணிகள் A மற்றும் B−க்குப் பொதுவாக
• (A ± B)2 என்பது A2 ± 2AB + B2 −க்கு சமமாக இருக்க வேண்டிய அவசியமில்லை
• A2 – B2 என்பது (A + B) (A − B) −க்கு சமமாக இருக்க வேண்டிய அவசியமில்லை
எடுத்துக்காட்டு 7.10
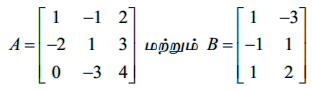 எனில் AB மற்றும் BA ஆகியவற்றை இயலுமெனில் காண்க.
எனில் AB மற்றும் BA ஆகியவற்றை இயலுமெனில் காண்க.
தீர்வு
A −ன் வரிசை 3 × 3 மற்றும் B−இன் வரிசை 3 × 2. எனவே AB −இன் வரிசை 3 × 2 ஆகும். A, B என்ற அணிகள் பெருக்கல் AB காண C = AB என்க.
c11 = (A −இன் முதல் நிரை) (B −ன் முதல் நிரல்)
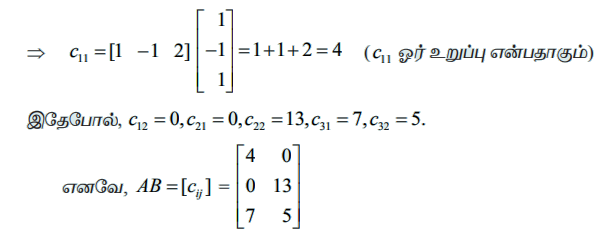
B என்ற அணியில் உள்ள நிரல்களின் எண்ணிக்கை, A அணியின் நிரைகளின் எண்ணிக்கைக்குச் சமமல்ல என்பதால் BA−ஐக் காண முடியாது.
எடுத்துக்காட்டு 7.11
ஒரு பழவியாபாரி 3 வெவ்வேறு வகையான பரிசுத் தொகுப்புகளைத் தயார் செய்கிறார். தொகுப்பு I−ல், 6 ஆப்பிள், 3 ஆரஞ்சு மற்றும் 3 மாதுளை உள்ளன. தொகுப்பு II−ல், 5 ஆப்பிள், 4 ஆரஞ்சு மற்றும் 4 மாதுளை உள்ளன. தொகுப்பு III−ல் 6 ஆப்பிள், 6 ஆரஞ்சு மற்றும் 6 மாதுளை உள்ளன. ஓர் ஆப்பிள், ஓர் ஆரஞ்சு மற்றும் ஒரு மாதுளை ஆகியவற்றின் விலை முறையே ₹ 30, ₹ 15 மற்றும் ₹ 45 எனில், ஒவ்வொரு பழத் தொகுப்பையும் தயார் செய்ய ஆகும் செலவு எவ்வளவு?
தீர்வு
விலை அணி A = [30 15 45],

AB என்ற அணியை காண்பதன் மூலம் பழத் தொகுப்புகளின் விலைகளைக் காணலாம்.
அதாவது, A−இல் உள்ள ஒவ்வொரு உருப்படியின் விலையுடன் (விலை அணி A) B−இல் உள்ள உருப்படிகளின் எண்ணிக்கையைப் (பழ அணி B) பெருக்குவதால் பழத்தொகுப்புகளின் விலைகளைப் பெறலாம்.
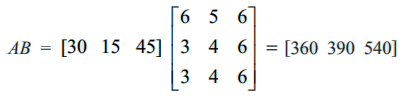
எனவே தொகுப்பு I−ன் விலை ₹ 360, தொகுப்பு II−ன் விலை ₹ 390, தொகுப்பு III−ன் விலை ₹ 540.
4. அணிக்கூட்டல், அணியை திசையிலியால் பெருக்குதல் மற்றும் அணிப்பெருக்கல் ஆகியவற்றின் பண்புகள் (Properties of matrix addition, scalar multiplication and Product of Matrices)
A, B, C என்பன சமவரிசையுடைய கூட்டலுக்கு உகந்த மூன்று அணிகள் மற்றும் a, b என்பன திசையிலிகள் என்க. இப்போது,
(1) A + B என்பது அதே வரிசையுடைய அணியைக் கொடுக்கும்.
(2) A + B = B + A (அணிக்கூட்டல் பரிமாற்றுப் பண்புடையது)
(3) (A + B) + C = A + (B + C) (அணிக்கூட்டல் சேர்ப்புத் தன்மையுடையது)
(4) A + O = O + A = A (O என்பது கூட்டல் சமனி)
(5) A + (− A) = O = (− A) + A (− A என்பது கூட்டலைப் பொறுத்து A−ன் எதிர்மறை அணியாகும்).
(6) (a + b)A = a A + bA மற்றும் a (A + B) = a A + aB
(7) a (bA) = (a b)A, 1A = A மற்றும் 0A = O.
அணிகளின் பெருக்கல் பண்புகள் (Properties of matrix multiplication)
அணிகளின் இயற்கணிதப் பண்புகளில் இருந்து பின்வருவனவற்றைப் பெறலாம்.
• A, B, C என்பன முறையே m × n, n × p மற்றும் p × q வரிசைகள் உடைய மூன்று அணிகள் எனில், A(BC) மற்றும் (AB)C என்பன m × q என்ற ஒரே வரிசை உடைய அணிகளாகும். மேலும்
A(BC) = (AB)C (அணிகளின் பெருக்கல் சேர்ப்புத் தன்மையுடையது).
• A, B, C என்பன முறையே m × n, n × p மற்றும் n × p வரிசைகள் உடைய மூன்று அணிகள் எனில், A(B + C) மற்றும் AB + AC என்பன m × p என்ற ஒரே வரிசை உடைய அணிகளாகும். மேலும் A(B + C) = AB + AC. (அணிகளின் பெருக்கல் கூட்டலைப் பொறுத்து இடது பங்கீட்டுத் தன்மையுடையது)
• A, B, C என்பன முறையே m × n, m × n மற்றும் n × p வரிசைகள் உடைய மூன்று அணிகள் எனில், (A + B)C மற்றும் AC + BC என்பன m × p என்ற சமவரிசை உடைய அணிகளாகும். மேலும் (A + B)C = AC + BC. (அணிகளின் பெருக்கல் கூட்டலைப் பொறுத்து வலது பங்கீட்டுத் தன்மையுடையது).
• A, B என்பன முறையே m × n, n × p வரிசைகள் உடைய இரண்டு அணிகள் மற்றும் α ஒரு திசையிலி எனில், α(AB) = A(α B) = (α A)B என்பது m × p வரிசை உடைய ஓர் அணியாகும்.
• I என்பது ஓர் அலகு அணி எனில், AI = IA = A (I என்பது பெருக்கல் சமனி).
5. நிரை நிரல் அணியின் மீதான செயல்முறைகள் மற்றும் அதன் பண்புகள் (Operation of transpose of a matrix and its properties)
வரையறை 7.16
ஓர் அணி A−ன் நிரை மற்றும் நிரல்களை இடமாற்றம் செய்வதன் மூலம் பெறப்படும் அணி A−ன் நிரை நிரல் மாற்று அணி எனப்படும். இது AT எனக் குறிக்கப்படும்.
அதாவது, A = [aij]m×n எனில், AT = [bij]n×m இங்கு bij = aji ஆகும். மேலும் AT −ன் (i,j) –ஆவது உறுப்பு aji ஆகும்.
எடுத்துக்காட்டாக,

இப்பொழுது நாம், வெளிப்படையான நிரூபணங்களைக் கொண்ட நிரை நிரல் மாற்று அணிக்கான சில அடிப்படை முடிவுகளைக் காண்போம்.
A, B என்பன உகந்த வரிசைகள் உடைய இரு அணிகள் எனில்,
(i) (AT) T = A
(ii) (kA) T = kAT (இங்கு k ஒரு திசையிலி)
(iii) (A + B) T = AT + BT
(iv) (AB) T = BTAT (நிரை நிரல் மாற்று அணியின் பின் திருப்புகை விதி)
எடுத்துக்காட்டு 7.12

6. சமச்சீர் மற்றும் எதிர் சமச்சீர் அணிகள் (Symmetric and skew−symmetric matrices)
வரையறை 7.17
A என்பது ஒரு சதுர அணி என்க. AT = A எனில், A என்பது சமச்சீர் அணியாகும்.
அதாவது, A = [aij]m×n என்பது ஒரு சமச்சீர் அணி எனில், அனைத்து i, j −க்கு aij = aji ஆகும்.
எடுத்துக்காட்டாக, 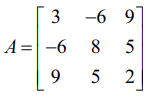 என்ற அணிக்கு AT = A என்பதால், இவ்வணி ஒரு சமச்சீர் அணியாகும்.
என்ற அணிக்கு AT = A என்பதால், இவ்வணி ஒரு சமச்சீர் அணியாகும்.
AT என்ற அணியின் நிரை நிரல் மாற்று அணி A என்ற அணியேயாகும் என்பதை கவனிக்கவும். அதாவது (AT) T = A.
வரையறை 7.18
A என்ற சதுர அணிக்கு AT = −A எனில், அவ்வணி எதிர் சமச்சீர்அணி எனப்படும்.
A = [aij]m×n என்பது எதிர் சமச்சீர்அணி எனில், அனைத்து i, j −க்கு aij = − aji ஆகும்.
i = j எனப்பிரதியிட்டால், 2aii = 0 அல்லது aii = 0 ∀ i
அதாவது, ஓர் எதிர் சமச்சீர் அணியில் மூலைவிட்ட உறுப்புகள் அனைத்தும் பூஜ்ஜியமாகும் என்பதே இதன் பொருளாகும்.
எடுத்துக்காட்டாக, 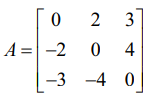 என்ற அணிக்கு AT = −A என்பதால், இவ்வணி ஓர் எதிர் சமச்சீர் அணியாகும்.
என்ற அணிக்கு AT = −A என்பதால், இவ்வணி ஓர் எதிர் சமச்சீர் அணியாகும்.
மேலும் எந்தவொரு சதுர அணியையும் சமச்சீர் மற்றும் எதிர் சமச்சீர் அணிகளின் கூடுதலாக எழுதலாம் என்பதைக் கவனிக்கவும்.
தேற்றம் 7.1
A என்பது மெய்யெண் மூலகங்களைக் கொண்ட ஒரு சதுர அணி எனில், A + AT என்பது ஒரு சமச்சீர் அணியாகும். மற்றும் A − AT என்பது ஓர் எதிர் சமச்சீர் அணியாகும்.
நிரூபணம்
B = A + AT என்க
BT = (A + AT) T = AT + (AT)T = AT + A = A + AT = B
எனவே (A+AT) ஒரு சமச்சீர் அணியாகும்.
C = A − AT என்க
CT = (A + (−AT ))T = AT + (−AT)T = AT − (AT) T = AT − A = −(A-AT) = −C
எனவே A − AT என்பது ஓர் எதிர் சமச்சீர் அணியாகும்.
தேற்றம் 7.2
ஒரு சதுர அணியை சமச்சீர் மற்றும் எதிர் சமச்சீர் அணிகளின் கூடுதலாக எழுதலாம்.
நிரூபணம்
A என்பது ஒரு சதுர அணி என்க.
A = ½ (A + AT) + ½ ( A − AT) என எழுதலாம்.
தேற்றம் 7.1 லிருந்து (A + AT) மற்றும் ( A − AT) என்பன முறையே சமச்சீர் மற்றும் எதிர் சமச்சீர் அணிகளாகும். (kA)T = kAT என்பதிலிருந்து ½ (A + AT) மற்றும் ½ ( A − AT) ஆகியவை முறையே சமச்சீர் மற்றும் எதிர் சமச்சீர் அணிகள் ஆகும். இதிலிருந்து தேவையான முடிவினைப் பெறலாம். இதன் மூலம் தேற்றம் நிரூபிக்கப்படுகிறது.
குறிப்பு 7.4
சமச்சீர் மற்றும் எதிர் சமச்சீர் அணியாக உள்ள அணி பூஜ்ஜிய அணியாகும்.
எடுத்துக்காட்டு 7.13

ஆகவே A என்பதை ஒரு சமச்சீர் மற்றும் எதிர் சமச்சீர் அணிகளில் கூடுதலாக எழுதலாம்.