11 வது கணக்கு : அலகு 7 : அணிகளும் அணிக்கோவைகளும் (Matrices and Determinants)
அணிக்கோவைகளின் பண்புகள் (Properties of Determinants)
அணிக்கோவைகளின் பண்புகள் (Properties of Determinants)
அணிக்கோவைகளின் மதிப்புக் காண, பின்வரும் அணிக்கோவையின் பண்புகளில் ஒன்று அல்லது அதற்கு மேற்பட்டவற்றைப் பயன்படுத்தலாம்.
பண்பு 1
ஓர் அணிக்கோவையின் நிரைகளை நிரல்களாகவும், நிரல்களை நிரைகளாகவும் இடமாற்றம் செய்தால் அதன் மதிப்பு மாறாது. அதாவது,| A | = | AT | .
ஓர் அணிக்கோவையில் நிரைவழி விரிவு காண்பதும், நிரல் வழி விரிவு காண்பதும் சமம் என்பதிலிருந்து இப்பண்பு உண்மையாகிறது.
பண்பு 2
ஓர் அணிக்கோவையின் ஏதேனும் இரு நிரைகள் (அல்லது நிரல்கள்) இடமாற்றம் செய்யப்படும்போது, அணிக்கோவையின் குறி மாறும். ஆனால் எண்ணளவு மாறாது.
சரிபார்த்தல்
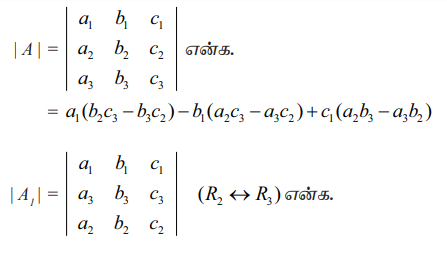
= a1(b3c2 – b2c3) − b1(a3c2 – a2c3) + c1(a3b2 – a2b3)
= – a1(b2c3 – b3c2) − b1(a2c3 – a3c2) – c1(a2b3 – a3b2)
= – [a1(b2c3 – b3c2) − b1(a2c3 – a3c2) + c1(a2b3 – a3b2)]
= − | A|
| A1| = − | A|
பண்பு 3
A என்ற அணியின் n நிரைகள் (நிரல்கள்) இடமாற்றம் செய்யப்படின், அவ்வணியின் அணிக்கோவை (−1)n |A| ஆகும்.
பண்பு 4
ஓர் அணிக்கோவையில் இரு நிரைகள் (அல்லது நிரல்கள்) சர்வ சமம் எனில், அவ்வணிக்கோவையின் மதிப்பு பூஜ்ஜியமாகும்.
சரிபார்த்தல்
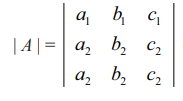 என்க. இரண்டாம் மற்றும் மூன்றாம் நிரைகள் சர்வ சமம் எனக் கொள்க.
என்க. இரண்டாம் மற்றும் மூன்றாம் நிரைகள் சர்வ சமம் எனக் கொள்க.
இரண்டாம் மற்றும் மூன்றாம் நிறைகளைப் பரிமாற்றம் செய்யக் கிடைப்பது
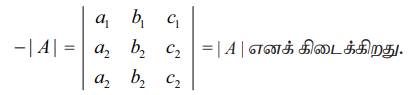
⇒ 2|A| = 0 ⇒ | A | = 0.
பண்பு 5
A என்ற அணியின் ஒரு நிரை (அல்லது நிரல்) அவ்வணியின் மற்றொரு நிரையின் (அல்லது நிரலின்) திசையிலிப் பெருக்கலாக இருப்பின், அதன் அணிக்கோவையின் மதிப்பு பூஜ்ஜியமாகும்.
குறிப்பு 7.8
(i) ஓர் அணிக்கோவையின் ஒரு நிரை அல்லது நிரலில் உள்ள அனைத்து உறுப்புகளும் பூஜ்ஜியம் எனில், அவ்வணிக் கோவையின் மதிப்பு பூஜ்ஜியமாகும்.
(ii) ஒரு முக்கோண வடிவ அணியின் அணிக்கோவையின் மதிப்பானது அதன் முதன்மை மூலைவிட்ட உறுப்புகளின் பெருக்கற்பலனாகும்.
பண்பு 6
ஓர் அணிக்கோவையில் ஏதேனும் ஒரு நிரையில் (நிரலில்) உள்ள ஒவ்வொரு உறுப்பும் ஒரு திசையிலி kஆல் பெருக்கப்பட்டிருப்பின் அந்த அணிக்கோவையின் மதிப்பு kஆல் பெருக்கப்பட்டதாக அமையும்.
சரிபார்த்தல்
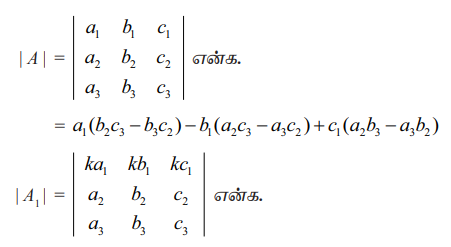
= ka1(b2c3 – b3c2) − kb1(a2c3 – a3c2) + kc1(a2b3 – a3b2) = k| A|
= k[a1(b2c3 – b3c2) − b1(a2c3 – a3c2) + c1(a2b3 – a3b2)]= k| A|
⇒ |A1| = k |A|
குறிப்பு 7.9
(i) A என்பது வரிசை n உடைய சதுர அணி எனில்,
(ii) |AB| = |A| |B|
(iii) AB = O எனில், | A | = 0 அல்லது | B | = 0.
(iv) | An | = (| A |)n
பண்பு 7
ஓர் அணிக்கோவையில் உள்ள ஒரு நிரையின் (நிரலின்) ஒவ்வொரு உறுப்பும் இரண்டு அல்லது அதற்கு மேற்பட்ட உறுப்புகளின் கூடுதலாக இருக்குமெனில், அவ்வணிக்கோவையை இரண்டு அல்லது அதற்கு மேற்பட்ட அணிக்கோவைகளின் கூட்டல் பலனாக எழுத இயலும்.
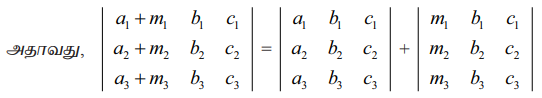
சரிபார்த்தல்
முதல் நிரல் வழியாக விரிவுபடுத்த
LHS = (a1+ m1) (b2c3 – b3c2) − (a2 + m2)(b1c3 – b3c1) + (a3+ m3) (b1c2 – b2c1)
= a1 (b2c3 – b3c2) − a2 (b1c3 – b3c1) + a3(b1c2 – b2c1) + m1(b2c3 – b3c2) – m2 (b1c3 – b3c1) + m3(b1c2 – b2c1)
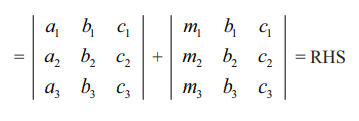
பண்பு 8
ஓர் அணிக்கோவையில் ஒரு நிரையில் (நிரலில்) உள்ள ஒவ்வொரு உறுப்போடும் மற்ற பிற நிரைகளில் (நிரல்களில்) உள்ள ஒத்த உறுப்புகளைக் குறிப்பிட்ட மாறிலிகளால் முறையே பெருக்கிக் கூட்டுவதால் அல்லது கழிப்பதால் அவ்வணிக் கோவையின் மதிப்பு மாறாது.
சரிபார்த்தல்
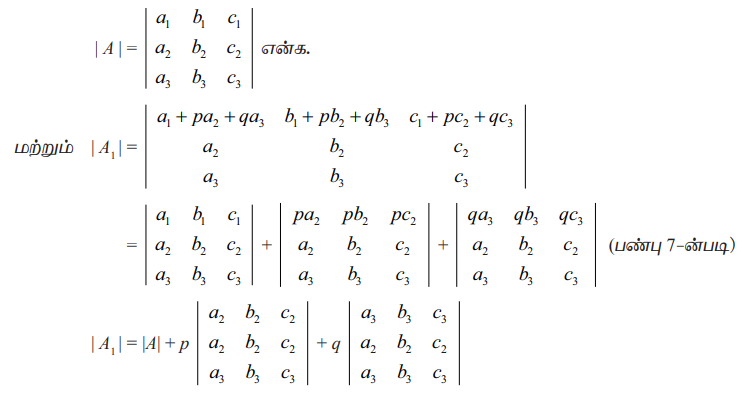
| A1| = | A | + p(0) + q(0) = |A| (பண்பு 4 −ன்படி)
| A1| = | A |
இப்பண்பு ஒரு குறிப்பிட்ட நிறையை அல்லது நிரலைச் சார்ந்தது அல்ல.
எடுத்துக்காட்டு 7.18