விளக்க எடுத்துக்காட்டு - அணிகளின் மீதான இயற்கணிதச் செயல்முறைகள் (Algebraic Operations on Matrices) | 11th Mathematics : UNIT 7 : Matrices and Determinants
11 வது கணக்கு : அலகு 7 : அணிகளும் அணிக்கோவைகளும் (Matrices and Determinants)
அணிகளின் மீதான இயற்கணிதச் செயல்முறைகள் (Algebraic Operations on Matrices)
அணிகளின் மீதான இயற்கணிதச் செயல்முறைகள் (Algebraic Operations on Matrices)
இப்பகுதியில் அணிகளின் அடிப்படைச் செயல்களான
(1) ஓர் அணியை திசையிலியால் பெருக்குதல்
(2) அணிகளின் கூட்டல் மற்றும் கழித்தல்
(3) அணிகளின் பெருக்கல்
ஆகியவற்றைப் பார்ப்போம்.
ஓர் அணியை மற்றோர் அணியால் வகுத்தல் பற்றிய கருத்தாக்கம் வரையறுக்கப்படவில்லை. எனவே, A, B என்ற ஏதேனும் இரண்டு அணிகளுக்கு A/B என்ற செயல்பாடு வரையறுக்கப்படவில்லை.
(1) ஓர் அணியைத் திசையிலியால் பெருக்குதல்
ஓர் அணி A = [aij]m×n மற்றும் k என்பது மெய் திசையிலி என்க. இப்போது, kA = [bij]m×n என்ற புதிய அணியை வரையறுப்போம். இங்கு, அனைத்து i, j−க்கு bij = kaij ஆகும்.
எடுத்துக்காட்டாக, A = 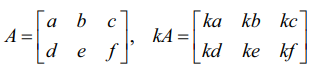
குறிப்பாக, k = −1 எனில், −A=[−aij]m×n எனப்பெறுகிறோம். இந்த − A என்பது A என்ற அணியின் எதிர்மறை அணி எனப்படும்.
(2) இரண்டு அணிகளின் கூட்டல் மற்றும் கழித்தல்
A, B என்பவை ஒரே வரிசையுடைய இரு அணிகள் எனில் இவற்றின் கூடுதல் அதே வரிசையுள்ள அணியாகும். இவ்வணி A + B எனக் குறிக்கப்பட்டு A, B−ன் ஒத்த உறுப்புகளைக் கூட்டுவதன் மூலம் பெறப்படுகிறது.
A = [aij]m×n , B = [bij]m×n என்ற இரு அணிகளின் கூடுதல் A + B = [cij]m×n என்ற அணியாகும். இங்கு அனைத்து i, j−க்கு cij = aij + bij ஆகும்.
இதேபோல், கழித்தல் A − B ஆனது A − B = A + (−1)B என வரையறுக்கப்படுகிறது
அதாவது, A – B = [dij]m×n , இங்கு dij = aij − bij , ∀ i மற்றும் j.
(∀ என்ற குறியீடு ஒவ்வொரு அல்லது அனைத்து எனப் பொருள்படும்).
குறிப்பு 7.2
A, B என்ற அணிகளின் வரிசைகள் சமமற்றவை எனில், A + B மற்றும் A − B என்பவற்றை வரையறுக்க இயலாது.
அணிகளின் கூட்டல் மற்றும் கழித்தல் செயல்களை எந்த ஒரு முடிவுறு எண்ணிகையுள்ள அணிகளுக்கும் விரிவுபடுத்தலாம்.
எடுத்துக்காட்டு 7.4
 எனில், A + B மற்றும் A – B ஆகியவற்றைக் காண்க.
எனில், A + B மற்றும் A – B ஆகியவற்றைக் காண்க.
தீர்வு
அணிகளின் கூட்டல் மற்றும் கழித்தல் வரையறைகளின்படி,

எடுத்துக்காட்டு 7.5

(3) அணிகளின் பெருக்கல்
வரையறை 7.15
A என்ற அணியின் நிரல்களின் எண்ணிக்கையும் B என்ற அணியின் நிரல்களின் எண்ணிக்கையும் சமமாக இருப்பின் A என்ற அணி B என்ற அணியுடன் பெருக்கலுக்கு உகந்தது எனப்படும்.
அதாவது, A = [aij]m×n மற்றும் B = [bij]n×p என்பன இரு அணிகள் எனில், இவ்வணிகளின் பெருக்கல் AB எனக்குறிப்பிடப்படும். மேலும் இதன் வரிசை m × p ஆகும்.

எடுத்துக்காட்டு 7.8

குறிப்பு 7.3
(1) A = [aij]m×n , B = [bij]n×p, மற்றும் m ≠ p, எனில் AB என்ற பெருக்கல் அணியை வரையறுக்க முடியும். ஆனால் BA−ஐ காண முடியாது.
(2) மெய்யெண்களின் பின்வரும் அடிப்படைப் பண்புகள் அணிகளிலும் விவாதிக்கப்படுகிறது.
அதாவது,
ab = ba ∀a, b ∈ ℝ
ab = ac ⇒ b = c ∀ a,b,c ∈ ℝ , a ≠ 0
ab = 0 ⇒ a = 0 அல்லது b = 0 ∀ a,b ∈ ℝ
இதேப்போன்று அணிகளிலும் விவாதிக்கலாம். அதாவது,
(i) AB மற்றும் BA என்பவை வரையறுக்கப்பட்டிருந்தாலும், AB = BA ஆக இருக்கவேண்டிய அவசியமில்லை.
எடுத்துக்காட்டாக,
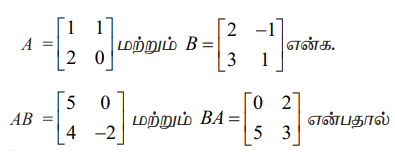
AB ≠ BA, எனக் காண்கிறோம்.
இந்நிலையில், A, B என்ற அணிகள் பெருக்கலைப் பொறுத்து பரிமாற்றுப் பண்பை பெறவில்லை என்கிறோம்.
மேலும் AB = BA என்பதும் சில நேரங்களில் உண்மையாகும். எடுத்துக்காட்டாக,
 எனக் காண்கிறோம்.
எனக் காண்கிறோம்.
(ii) அணிப்பெருக்கலில் நீக்கல் பண்பு உண்மையாகாது. அதாவது, n × n, n > 1 என்ற வரிசை உடைய A ≠ 0, B, C என்ற மூன்று சதுர அணிகளுக்கு, AB = AC எனில், B = C, மற்றும் BA = CA எனில், B = C என்பவை உண்மையாக இருக்கவேண்டிய அவசியமில்லை.
இவ்வுண்மைகளை, பின்வரும் எளிய எடுத்துக்காட்டின் மூலம் காணலாம்.
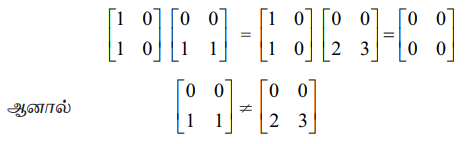
(iii) A ≠ 0 மற்றும் B ≠ 0 ஆக இருந்து AB = 0 ஆக வாய்ப்புள்ளது. அதாவது, AB = 0 எனில், A = 0 அல்லது B = 0 ஆக இருக்க வேண்டிய அவசியமில்லை. எடுத்துக்காட்டாக,
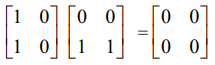
(3) கீழே கொடுக்கப்பட்டுள்ள அணிகளின் கூட்டல் மற்றும் பெருக்கல் செயல்களுக்கு உகந்த ஏதேனும் இரு அணிகள் A மற்றும் B−க்குப் பொதுவாக
• (A ± B)2 என்பது A2 ± 2AB + B2 −க்கு சமமாக இருக்க வேண்டிய அவசியமில்லை
• A2 – B2 என்பது (A + B) (A − B) −க்கு சமமாக இருக்க வேண்டிய அவசியமில்லை
எடுத்துக்காட்டு 7.10
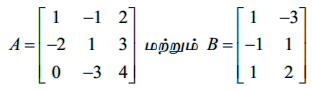 எனில் AB மற்றும் BA ஆகியவற்றை இயலுமெனில் காண்க.
எனில் AB மற்றும் BA ஆகியவற்றை இயலுமெனில் காண்க.
தீர்வு
A −ன் வரிசை 3 × 3 மற்றும் B−இன் வரிசை 3 × 2. எனவே AB −இன் வரிசை 3 × 2 ஆகும். A, B என்ற அணிகள் பெருக்கல் AB காண C = AB என்க.
c11 = (A −இன் முதல் நிரை) (B −ன் முதல் நிரல்)
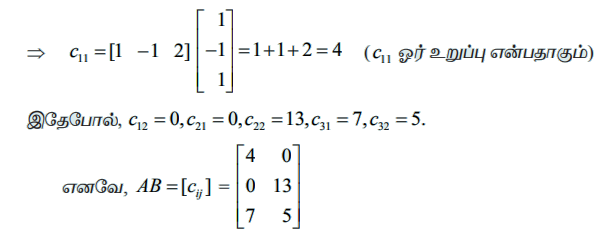
B என்ற அணியில் உள்ள நிரல்களின் எண்ணிக்கை, A அணியின் நிரைகளின் எண்ணிக்கைக்குச் சமமல்ல என்பதால் BA−ஐக் காண முடியாது.
எடுத்துக்காட்டு 7.11
ஒரு பழவியாபாரி 3 வெவ்வேறு வகையான பரிசுத் தொகுப்புகளைத் தயார் செய்கிறார். தொகுப்பு I−ல், 6 ஆப்பிள், 3 ஆரஞ்சு மற்றும் 3 மாதுளை உள்ளன. தொகுப்பு II−ல், 5 ஆப்பிள், 4 ஆரஞ்சு மற்றும் 4 மாதுளை உள்ளன. தொகுப்பு III−ல் 6 ஆப்பிள், 6 ஆரஞ்சு மற்றும் 6 மாதுளை உள்ளன. ஓர் ஆப்பிள், ஓர் ஆரஞ்சு மற்றும் ஒரு மாதுளை ஆகியவற்றின் விலை முறையே ₹ 30, ₹ 15 மற்றும் ₹ 45 எனில், ஒவ்வொரு பழத் தொகுப்பையும் தயார் செய்ய ஆகும் செலவு எவ்வளவு?
தீர்வு
விலை அணி A = [30 15 45],

AB என்ற அணியை காண்பதன் மூலம் பழத் தொகுப்புகளின் விலைகளைக் காணலாம்.
அதாவது, A−இல் உள்ள ஒவ்வொரு உருப்படியின் விலையுடன் (விலை அணி A) B−இல் உள்ள உருப்படிகளின் எண்ணிக்கையைப் (பழ அணி B) பெருக்குவதால் பழத்தொகுப்புகளின் விலைகளைப் பெறலாம்.
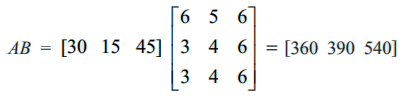
எனவே தொகுப்பு I−ன் விலை ₹ 360, தொகுப்பு II−ன் விலை ₹ 390, தொகுப்பு III−ன் விலை ₹ 540.