அணிக்கோவைகள் (Determinants)

அணிக்கோவைகள் (Determinants)

n வரிசையுள்ள ஒவ்வொரு சதுர அணி A உடன், நாம் அணி A−ன் அணிக்கோவை என்ற எண்ணைத் தொடர்புபடுத்தலாம்.

குறிப்பு 7.5

(i) சதுர அணிகளுக்கு மட்டுமே அணிக்கோவைகளை வரையறுக்க முடியும்.

(ii) ஒரு சதுர அணி A−ன் அணிக்கோவையை | A| எனக் குறிக்கிறோம்.

(இதனை அணிக்கோவை A எனப்படிக்கவும்)

(iii) ஓர் அணி என்பது வடிவமைப்பு மட்டுமே. ஆனால், அணிக்கோவை ஒரு மதிப்பைப் பெற்றிருக்கும்.

1. பல்வேறு வரிசைகள் உடைய அணியின் அணிக்கோவைகள் (Determinants of matrices of different order)

வரிசை 1 உடைய அணியின் அணிக்கோவை

A = [a] என்பது வரிசை 1 உடைய அணி எனில், A−ன் அணிக்கோவை ‘a’ என வரையறுக்கப்படுகிறது.

வரிசை 2 உடைய அணியின் அணிக்கோவை

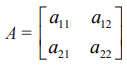என்பது வரிசை 2 உடைய அணி எனில், A−ன் அணிக்கோவை

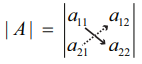= a11 a22 – a21 a12 என வரையறுக்கப்படுகிறது.

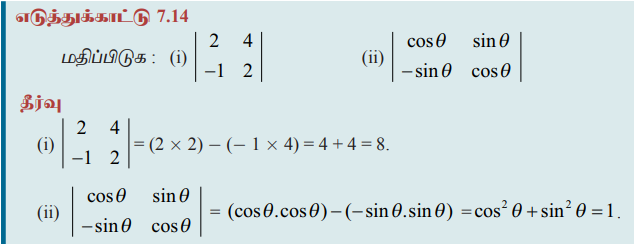
வரிசை 3 உடைய அணியின் அணிக்கோவை

மெய்யெண்கள் அல்லது ℝ −ல் வரையறுக்கப்பட்ட மெய் மதிப்புகளையுடைய சார்புகளை உறுப்புகளாகக் கொண்ட 3 × 3 வரிசையுடைய அணிக்கோவையை எடுத்துக்கொண்டு, அதன் பண்புகளைப் பற்றிப் படிப்பதுடன் அணிக்கோவைகளின் மதிப்புகளைக் காணும் பல்வேறு முறைகள் குறித்தும் விவாதிப்போம்.

வரையறை 7.19

A = [aij]3×3 என்பது 3−ஆம் வரிசையுடைய சதுர அணி என்க. ஏதேனும் ஒரு உறுப்பு aij −ன் சிற்றணிக்கோவையானது aij உள்ள i−ஆவது நிரை மற்றும் j−ஆவது நிரலை நீக்குவதால் பெறப்படும் அணிக்கோவையாகும். aij −ன் சிற்றணிக்கோவையானது வழக்கமாக Mij எனக் குறிக்கப்படும்.

வரையறை 7.20

தகுந்த குறியிடப்பட்ட சிற்றணிக்கோவை இணைக்காரணி எனப்படும். aij −ன் இணைக்காரணி Aij எனக்குறிக்கப்படும். மேலும் Aij = (−1)i+j Mij என வரையறுக்கப்படும்.

எடுத்துக்காட்டாக 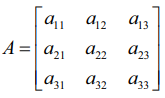என்பது 3 × 3 வரிசை உடைய அணி என்க.

இவ்வணியின் உறுப்புகள் a11 , a12, a13 ஆகியவற்றின் சிற்றணிக் கோவைகள் மற்றும் இணைக்காரணிகள் பின்வருமாறு:

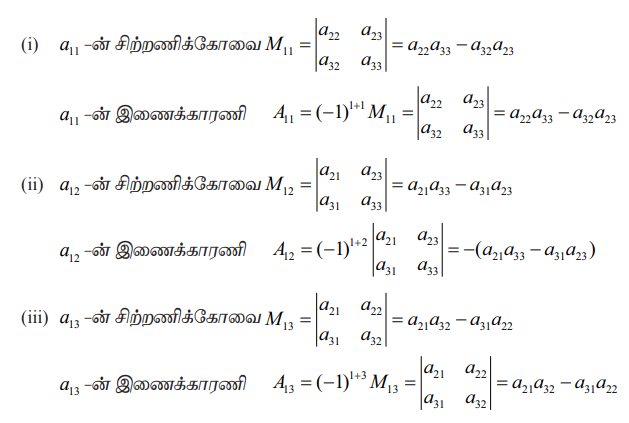
முடிவு 7.1 லாப்லாஸ் விரிவாக்கம் (Laplace Expansion)

கொடுக்கப்பட்ட A = [aij]3×3 என்ற அணியின் முதல் நிரையிலுள்ள உறுப்புகளை அவற்றின் ஒத்த இணைக்காரணிகளுடன் பெருக்கிக் கூடுதல் கண்டால், அது A−ன் அணிக்கோவைக்குச் சமமாகும். 

அதாவது, |A| = a11 A11  + a12 A12 + a13 A13     ….... (1)

இதனையே சிற்றணிக் கோவைகளின் வரையறையைப் பயன்படுத்தி பின்வருமாறு எழுதலாம். | A | = a11M11 − a12M12 + a13M13.

ஓர் அணிக்கோவையை எந்தவொரு நிரை அல்லது நிரல் வழியாகவும் விரிவுப்படுத்தலாம். இவ்வாறு காணப்படும் எல்லா விரிவாக்கங்களின் மதிப்புகள் அனைத்தும் சமமாக இருப்பதைக் கவனிக்கவும்.

எடுத்துக்காட்டாக,

R1 வழியாக விரிவுபடுத்த, |A| = a11 A11  + a12 A12 + a13 A13      

R2 வழியாக விரிவுபடுத்த, |A| = a21 A21  + a22 A22 + a23 A23      

C1 வழியாக விரிவுபடுத்த, |A| = a11 A11  + a21 A21 + a31 A31     

எடுத்துக்காட்டு 7.15

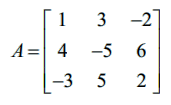எனில், A என்ற அணியின் அனைத்து சிற்றணிக்கோவைகள் மற்றும் இணைக்காரணிகளைக் காண்க. இவற்றைப் பயன்படுத்தி | A |−ஐக் காண்க. மேலும். எந்த ஒரு நிரை அல்லது நிரலைப் பயன்படுத்தி விரிவுபடுத்தினாலும் |A|−ன் மதிப்பு மாறுவதில்லை எனச்சரிபார்க்க. 

தீர்வு

சிற்றணிக்கோவைகள் :

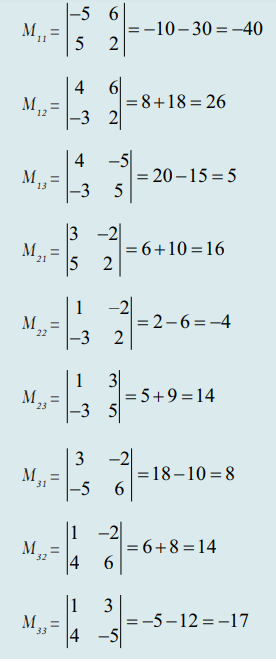
இணைக்காரணிகள் :

A11 = (−1)1+1 (−40) = −40

A12 = (−1)1+2 (+26) = −26

A13 = (−1)1+3 (5) = 5

A21= (−1)2+1 (16) = −16

A22 = (−1)2+2 (−4) = −4

A23 = (−1)2+3 (14) = −14

A31 = (−1)3+1 (8) = 8

A32 = (−1)3+2 (14) = −14

A33 = (−1)3+3(−17) = −17

R1 வழியாக விரிவுபடுத்த,

|A| =  a11 A11  + a12 A12 + a13 A13      

|A| = 1(−40) + (3) (−26) + (−2)(5) = −128     ……(3)

C1 வழியாக வரிவுபடுத்த,

|A| = a11 A11  + a21 A21 + a31 A31

= 1(−40) + 4(−16) + −3(8) = −128   …………..(4)

(3) மற்றும் (4) லிருந்து,

R1 வழியாக விரிவுபடுத்திப் பெறப்பட்ட |A| −ன் மதிப்பானது C1 வழியாக விரிவுபடுத்திப் பெற்ற | A |−ன் மதிப்புக்குச் சமம் என நிரூபணமாகிறது.

சாரஸ் விதியைப் பயன்படுத்தி வரிசை 3 உடைய அணிக்கோவையை மதிப்பிடல் (பிரெஞ்சுக் கணித மேதை பியாரே ப்ரடிக் சாரஸ் என்பவரது பெயரால் இவ்வாறு அழைக்கப்படுகிறது) (Evaluation of determinant of order 3 by using Sarrus Rule)

A என்ற அணியின் உறுப்புகளை பின்வருமாறு எழுதுக:

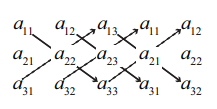
| A | ஆனது பின்வருமாறு கணக்கிடப்படுகிறது:

|A| = [a11 a22 a33 + a12 a23 a31 + a13 a21 a32] − [a33 a21 a12 + a32 a23 a11 + a31 a22 a13]

குறிப்பு 7.6

ஓர் அணிக்கோவையின் மதிப்பை எளிமையாகக் காண, அவ்வணிக்கோவையைப் பூஜ்ஜியங்கள் அதிகமாக உள்ள நிரை அல்லது நிரல் வழியாக விரிவுபடுத்தலாம்.

வரிசை n, n  ≥ 4 என உள்ள சதுர அணியின் அணிக்கோவை

அணிக்கோவைகளின் கருத்தாக்கத்தை வரிசை n, n ≥ 4 என உள்ள சதுர அணிகளுக்கும் விரிவுபடுத்தலாம். A =[aij]m×n , n ≥ 4 என்க.

A = [aij]m×n என்ற அணியின் அணிக்கோவையில் i ஆவது நிரை மற்றும் j ஆவது நிரலை நீக்கினால், வரிசை (n − 1) உடைய ஒரு அணிக்கோவை கிடைக்கும். இவ்வணிக்கோவை aij என்ற உறுப்பின் சிற்றணிக் கோவையாகும். இதனை Mij எனக்குறிக்கிறோம். aij −ன் இணைக்காரணி Aij = (−1)i+j Mij என வரையறுக்கப்படுகிறது.

முடிவு 7.2

வரிசை n உடைய சதுரஅணி A = [aij]m×n −ன் முதல் நிரையில் உள்ள உறுப்புகளையும் அவற்றின் ஒத்த இணைக்காரணிகளையும் பெருக்கிக் கூட்டினால், அது அணிக்கோவை A−க்கு சமமாகும். அதாவது,

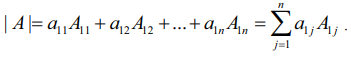இதற்குச் சமமாகச் சிற்றணிக் கோவைகள் மற்றும் இணைக்காரணிகளின் வரையறையைப் பயன்படுத்தி பின்வருமாறு எழுதலாம்.

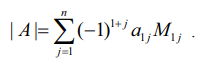
இங்கு A1j  என்பது a1j  −ன் இணைக்காரணி மற்றும் M1j  என்பது a1j  −ன் சிற்றணிக் கோவையாகும் j = 1, 2,… n  ஆகும்.

குறிப்பு 7.7

(i) A = [aij]m×n எனில், A−ன் அணிக்கோவையை det(A) அல்லது det A அல்லது ∆ எனக் குறிப்பிடலாம்.

(ii) இதனை, ஏதேனுமொரு நிரை அல்லது நிரலைப் பயன்படுத்தியும் கணக்கிடலாம்.

2. அணிக்கோவைகளின் பண்புகள் (Properties of Determinants)

அணிக்கோவைகளின் மதிப்புக் காண, பின்வரும் அணிக்கோவையின் பண்புகளில் ஒன்று அல்லது அதற்கு மேற்பட்டவற்றைப் பயன்படுத்தலாம்.

பண்பு 1

ஓர் அணிக்கோவையின் நிரைகளை நிரல்களாகவும், நிரல்களை நிரைகளாகவும் இடமாற்றம் செய்தால் அதன் மதிப்பு  மாறாது. அதாவது,| A | = | AT | . 

ஓர் அணிக்கோவையில் நிரைவழி விரிவு காண்பதும், நிரல் வழி விரிவு காண்பதும் சமம் என்பதிலிருந்து இப்பண்பு உண்மையாகிறது.

பண்பு 2

ஓர் அணிக்கோவையின் ஏதேனும் இரு நிரைகள் (அல்லது நிரல்கள்) இடமாற்றம் செய்யப்படும்போது, அணிக்கோவையின் குறி மாறும். ஆனால் எண்ணளவு மாறாது.

சரிபார்த்தல்

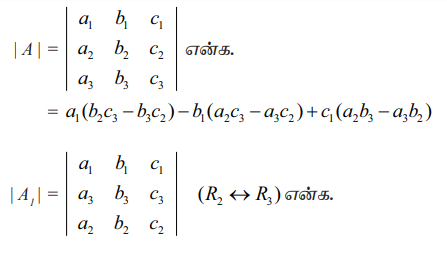
= a1(b3c2 – b2c3) − b1(a3c2 – a2c3) + c1(a3b2 – a2b3)

= – a1(b2c3 – b3c2) − b1(a2c3 – a3c2) – c1(a2b3 – a3b2)

= – [a1(b2c3 – b3c2) − b1(a2c3 – a3c2) + c1(a2b3 – a3b2)]

= − | A|

| A1| = − | A|

பண்பு 3

A என்ற அணியின் n நிரைகள் (நிரல்கள்) இடமாற்றம் செய்யப்படின், அவ்வணியின் அணிக்கோவை (−1)n |A| ஆகும்.

பண்பு 4

ஓர் அணிக்கோவையில் இரு நிரைகள் (அல்லது நிரல்கள்) சர்வ சமம் எனில், அவ்வணிக்கோவையின் மதிப்பு பூஜ்ஜியமாகும்.

சரிபார்த்தல்

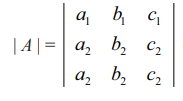என்க. இரண்டாம் மற்றும் மூன்றாம் நிரைகள் சர்வ சமம் எனக் கொள்க.

இரண்டாம் மற்றும் மூன்றாம் நிறைகளைப் பரிமாற்றம் செய்யக் கிடைப்பது

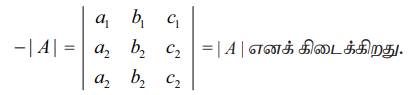
⇒ 2|A| = 0 ⇒ | A | = 0.

பண்பு 5

A என்ற அணியின் ஒரு நிரை (அல்லது நிரல்) அவ்வணியின் மற்றொரு நிரையின் (அல்லது நிரலின்) திசையிலிப் பெருக்கலாக இருப்பின், அதன் அணிக்கோவையின் மதிப்பு பூஜ்ஜியமாகும்.

குறிப்பு 7.8

(i) ஓர் அணிக்கோவையின் ஒரு நிரை அல்லது நிரலில் உள்ள அனைத்து உறுப்புகளும் பூஜ்ஜியம் எனில், அவ்வணிக் கோவையின் மதிப்பு பூஜ்ஜியமாகும்.

(ii) ஒரு முக்கோண வடிவ அணியின் அணிக்கோவையின் மதிப்பானது அதன் முதன்மை மூலைவிட்ட உறுப்புகளின் பெருக்கற்பலனாகும்.

பண்பு 6

ஓர் அணிக்கோவையில் ஏதேனும் ஒரு நிரையில் (நிரலில்) உள்ள ஒவ்வொரு உறுப்பும் ஒரு திசையிலி kஆல் பெருக்கப்பட்டிருப்பின் அந்த அணிக்கோவையின் மதிப்பு kஆல் பெருக்கப்பட்டதாக அமையும்.

சரிபார்த்தல்

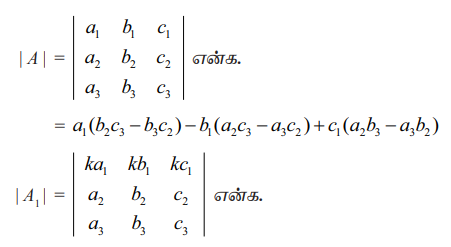
= ka1(b2c3 – b3c2) − kb1(a2c3 – a3c2) + kc1(a2b3 – a3b2) =   k| A|

= k[a1(b2c3 – b3c2) − b1(a2c3 – a3c2) + c1(a2b3 – a3b2)]=   k| A|

⇒ |A1| =  k |A|

குறிப்பு 7.9

(i) A என்பது வரிசை n உடைய சதுர அணி எனில்,

(ii) |AB| = |A| |B|

(iii) AB = O எனில், | A | = 0 அல்லது | B | = 0.

(iv) | An | = (| A |)n

பண்பு 7

ஓர் அணிக்கோவையில் உள்ள ஒரு நிரையின் (நிரலின்) ஒவ்வொரு உறுப்பும் இரண்டு அல்லது அதற்கு மேற்பட்ட உறுப்புகளின் கூடுதலாக இருக்குமெனில், அவ்வணிக்கோவையை இரண்டு அல்லது அதற்கு மேற்பட்ட அணிக்கோவைகளின் கூட்டல் பலனாக எழுத இயலும்.

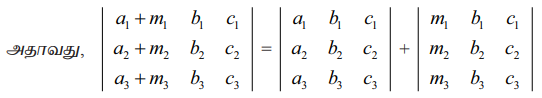
சரிபார்த்தல்

முதல் நிரல் வழியாக விரிவுபடுத்த

LHS = (a1+ m1) (b2c3 – b3c2) − (a2 + m2)(b1c3 – b3c1) + (a3+ m3) (b1c2 – b2c1) 

= a1 (b2c3 – b3c2) − a2 (b1c3 – b3c1)  + a3(b1c2 – b2c1) + m1(b2c3 – b3c2) – m2 (b1c3 – b3c1) + m3(b1c2 – b2c1)

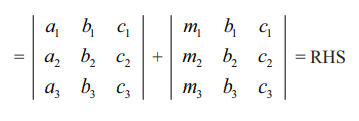
பண்பு 8

ஓர் அணிக்கோவையில் ஒரு நிரையில் (நிரலில்) உள்ள ஒவ்வொரு உறுப்போடும் மற்ற பிற நிரைகளில் (நிரல்களில்) உள்ள ஒத்த உறுப்புகளைக் குறிப்பிட்ட மாறிலிகளால் முறையே பெருக்கிக் கூட்டுவதால் அல்லது கழிப்பதால் அவ்வணிக் கோவையின் மதிப்பு மாறாது. 

சரிபார்த்தல்

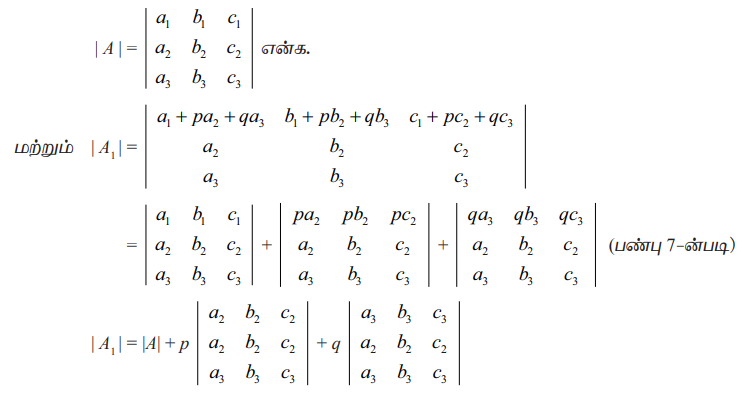
| A1| =  | A | + p(0) + q(0) = |A|   (பண்பு 4 −ன்படி)

| A1| =  | A | 

இப்பண்பு ஒரு குறிப்பிட்ட நிறையை அல்லது நிரலைச் சார்ந்தது அல்ல.

எடுத்துக்காட்டு 7.18