அணிக்கோவைகளுக்குக் காரணித் தேற்றத்தின் பயன்பாடு (Application of factor theorem to determinants)

அணிக்கோவைகளுக்குக் காரணித் தேற்றத்தின் பயன்பாடு (Application of factor theorem to determinants)

தேற்றம் 7.3 (காரணித்தேற்றம்) (Factor Theorem)

ஓர் அணி A−ன் ஒவ்வொரு உறுப்பும் x−ஆல் அமைந்த பல்லுறுப்புக் கோவையாக இருந்து, x = a எனப் பிரதியிட |A | −ன் மதிப்பு பூஜ்ஜியமாகும் எனில், (x − a) என்பது | A | −ன் ஒரு காரணியாகும். 

குறிப்பு 7.10

(i) ஓர் அணிக்கோவையின் மதிப்பைக் காரணிகளின் பெருக்கல் வடிவில் பெறுவதற்கு இத்தேற்றம் மிகவும் பயன்படுகிறது.

(ii) b= a என | A |−ல் பிரதியிட, அதன் ஏதேனும் இரு நிரைகள் அல்லது நிரல்கள் சர்வசமமானால், | A| = 0 ஆகும். எனவே காரணித் தேற்றத்தின்படி (a − b) என்பது | A |−ன் ஒரு காரணியாகும்.

(iii) n (n ≥ r) வரிசையுள்ள அணிக்கோவையில் x = a எனப் பிரதியிட, r நிரைகள் (நிரல்கள்) சர்வசமமானால், (x − a)r−1 என்பது | A | −ன் ஒரு காரணியாகும்.

(iv) ஒரு சதுர அணியின் (அல்லது அதன் அணிக்கோவை) ஒவ்வொரு நிரையும் முதல் நிரையில் உள்ள மாறிகளை வட்டச் சுழல் முறையில் மாற்றுவதன் மூலம் பெறப்பட்டால், அது வட்டச் சமச்சீர் வடிவம் எனப்படும்.

(v) ஒரு வட்டச் சமச்சீர் அணிக்கோவையில் m என்பது காரணிகளின் (பிரதியிடுவதால் பெறப்பட்ட) பெருக்கலின் படிக்கும் முதன்மை மூலைவிட்ட உறுப்புகளின் பெருக்கலின் படிக்கும் உள்ள வித்தியாசம் என்க.

(1) இப்போது m = 0 எனில் மேலும் தேவையான காரணி மாறிலி k ஆகும்.

(2) m = 1 எனில் மேலும் தேவையான காரணி k(a + b+ c) ஆகும்.

(3) m = 2 எனில் மேலும் தேவையான காரணி k(a2 + b2 + c2) + l(ab+ bc+ ca) ஆகும்.

எடுத்துக்காட்டு 7.23

காரணித் தேற்றத்தைப் பயன்படுத்தி 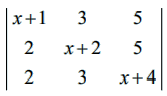= (x − 1)2(x + 9) என நிறுவுக.

தீர்வு

இங்கு மூன்று நிரைகளும் சர்வசமம். எனவே, (x – 1)2 ஆனது |A|−ன் ஒரு காரணியாகும்.

| A| −ல் x = −9 எனப் பிரதியிட,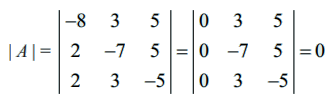

எனவே, (x + 9)ஆனது | A |−ன் காரணியாகும். [C1 → C1 + C2 + C3]

அதாவது (x − 1)2 (x + 9) என்பது |A|−ன் காரணியாகும். இதன் படி 3 ஆகும். அணிக்கோவை x−ல் அமைந்த 3−ம் படி பல்லுறுப்புக் கோவையாகும்.

எனவே, மீதமுள்ள மற்றொரு காரணி, மாறிலி ‘k’ ஆகும்.

ஆகவே, 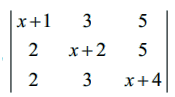  = k (x − 1)2(x + 9)

x3 உறுப்புகளை இருபுறமும் சமப்படுத்த, k = 1 எனப்பெறுகிறோம்.

எனவே, |A| = (x − 1)2 (x + 9)

எடுத்துக்காட்டு 7.24

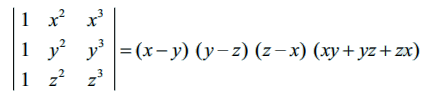என நிறுவுக.

தீர்வு

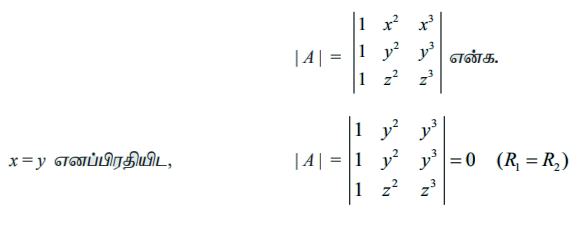
எனவே, (x − y) என்பது | A |−ன் ஒரு காரணியாகும்.

கொடுக்கப்பட்ட அணிக்கோவை x, y, z என்பவற்றில் வட்ட சமச்சீரானது. ஆகவே, (y − z) மற்றும் (z − x) ஆகியவையும் | A | −ன் காரணிகளாகும்.

இப்போது (x − y) (y − z) (z − x) என்பது | A |−ன் காரணியாகும். இதன் படி 3 ஆகும்.

முதன்மை மூலைவிட்ட உறுப்புகளின் பெருக்கல் 1 × y2 × z3 . இதன் படி 5 ஆகும்.

எனவே மீதமுள்ள மற்றொரு காரணி k(x2 + y2 + z2) + l(xy + yz + zx) ஆகும்.

எடுத்துக்காட்டு 7.25

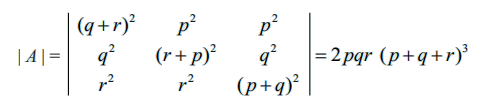என நிறுவுக.

தீர்வு

p = 0 எனப்பிரதியிட,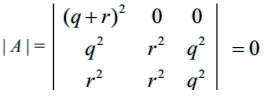

எனவே, (p – 0) என்பது ஒரு காரணியாகும். அதாவது p ஒரு காரணியாகும்.

| A | என்பது p, q, r என்பவற்றில் வட்டச் சமச்சீராகும். எனவே, q, r ஆகியவையும் | A | −ன் காரணிகளாகும்.

p + q + r = 0 எனில், q + r = −p ; r + p = −q; p + q = −r

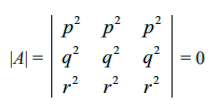எனப்பெறுகிறோம்.

இங்கு மூன்று நிரல்களும் சர்வசமம். எனவே, (p + q + r)2 என்பது | A |−ன் காரணியாகும்.

இப்போது pqr (p + q + r)2 என்பது | A |−ன் காரணியாகும். இதன் படி 5 ஆகும். | A |−ன் படி 6 ஆகும்.

எனவே, மற்றொரு காரணி k (p + q + r) ஆகும்.

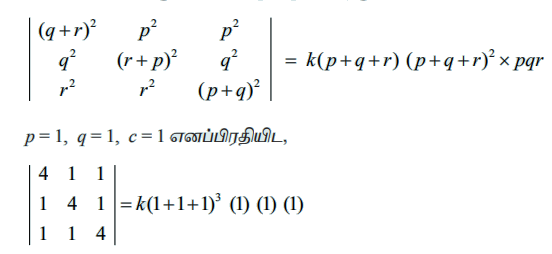
4(16 − 1) − 1(4 − 1) + 1(1 − 4) = 27k

60 − 3 − 3 = 27k ⇒ k = 2.

எனவே, |A| = 2pqr (p + q + r)3.

அதாவது, sin B= sin A எனில், சமன்பாடு நிறைவு செய்யப்படுகிறது.

இதேபோல் sin B= sin C மற்றும் sin C = sin A எனும்போதும் சமன்பாடு நிறைவு செய்யப்படுகிறது.

ஆகவே, A = Bஅல்லது B= C அல்லது C = A எனப்பெறுகிறோம்.

மேற்கண்ட எல்லா நிலைகளிலும் ஏதேனும் இரண்டு கோணங்கள் சமமாக உள்ளன. எனவே ∆ABC ஒரு இரு சமபக்க முக்கோணமாகும்.