பரப்பளவு

பரப்பளவு 

பொருள் ஒன்றின் மேற்புறப் பகுதியின் அளவு அதன் பரப்பளவு எனப்படும். வீட்டு மனை ஒன்றின் பரப்பளவைக் காண அதன் நீளம் மற்றும் அகலத்தைப் பெருக்க வேண்டும். 

பரப்பளவு = நீளம்  ×   அகலம் 

பரப்பளவின் அலகு மீ2  (இதனை சதுர மீட்டர் எனப் படிக்க வேண்டும்). பரப்பளவு என்பது அடிப்படை அளவான நீளத்தினை இரு முறை பெருக்கிக் கணக்கிடப்படுவதால் (நீளம்  ×   அகலம்) கிடைக்கும் வழி அளவாகும்.

ஒழுங்கான வடிவமுள்ள பொருள்களின் பரப்பளவு 

ஒழுங்கான வடிவமுள்ள பொருள்களின் பரப்பை தகுந்த சூத்திரங்களின் மூலம் கண்டறியலாம். ஒழுங்கான வடிவமுடைய சில பொருள்களின் கன அளவைக் கணக்கிட உதவும் சூத்திரங்கள் அட்டவணை 1.3ல் கொடுக்கப்பட்டுள்ளன

கணக்கு 1.1 

ஒரு மீட்டர் பக்க அளவு கொண்ட 10 சதுரங்களைக் கொண்ட பொருளொன்றின் பரப்பளவு என்ன? 

ஒரு சதுரத்தின் பரப்பளவு = பக்கம் ×  பக்கம் 

= 1மீ ×   1மீ

= 1 மீ2  (அ) 1 சதுர மீட்டர்

10 சதுரங்களைக் கொண்ட பொருளொன்றின் பரப்பளவு

= 1 சதுர மீட்டர் ×   10

  = 10 சதுர மீட்டர்

அட்டவணை 1.3 ஒழுங்கான வடிவமுள்ள பொருள்களின் பரப்பளவு

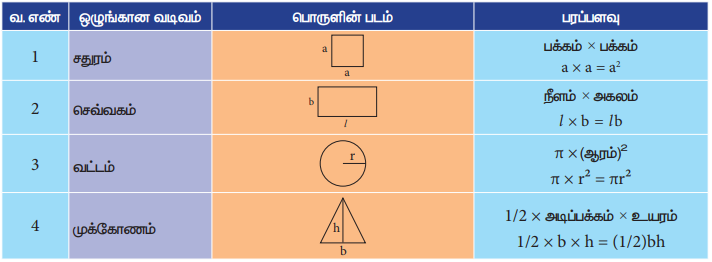
கணக்கு 1.2

 கீழே தரப்பட்டுள்ள ஒழுங்கான வடிவமுள்ள பொருள்களின் பரப்பளவைக் காணவும்: (π = 22/7 எனக் கொள்க)

அ. 12 செமீ  நீளமும், 4 செமீ  அகலமும் கொண்ட செவ்வகம் 

ஆ. 7 செமீ  ஆரம் கொண்ட வட்டம் 

இ. 6 செமீ அடிப்பக்கமும் 8 செமீ உயரமும் கொண்ட முக்கோணம்

தீர்வு 

அ.  செவ்வகத்தின் பரப்பு  = நீளம் × அகலம்= 12 ×  4 = 48 செமீ2

ஆ.  வட்டத்தின் பரப்பு        = π ×  r2 = 22/7 ×  7 ×  7 = 154 செமீ2

இ) முக்கோணத்தின் பரப்பு = 1/2 ×  அடிப்பக்கம் ×  உயரம் 

= 1/2 ×  6 ×  8 = 24 செமீ2

ஒழுங்கற்ற வடிவமுள்ள பொருள்களின் பரப்பளவு 

நாம் நமது அன்றாட வாழ்வில் இலைகள், மயில் இறகுகள் போன்ற பல ஒழுங்கற்ற வடிவமுள்ள பொருள்களைக் காண்கிறோம். இத்தகைய ஒழுங்கற்ற வடிவமுள்ள பொருள்களின் பரப்பளவினை நாம் சூத்திரத்தின் மூலம் கணக்கிட இயலாது.

இத்தகைய பொருள்களின் பரப்பளவினை நாம் எவ்வாறு காணலாம்? இது போன்ற ஒழுங்கற்ற வடிவமுள்ள பொருள்களின் பரப்பளவினை ஒரு வரைபடத்தாளைப் பயன்படுத்திக் காணலாம். ஒழுங்கற்ற வடிவமுள்ள பொருள்களின் பரப்பளவினை ஒரு வரைபடத்தாளைப் பயன்படுத்தி எவ்வாறு காணலாம் என்பதை செயல்பாடு 1 விளக்குகிறது.

செயல்பாடு:1

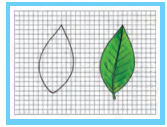
ஏதேனும் ஒரு மரத்திலிருந்து ஓர் இலையை எடுத்துக் கொள்க. அந்த இலையை ஒரு வரைபடத் தாளின் மீது வைத்து, அதன் எல்லையை ஒரு பென்சிலைக் கொண்டு வரைந்து கொள்க. இலையை நீக்கினால், அதன் எல்லையை வரைபடத் தாளின் மீது காணலாம்.

அ) இப்போது, இலையின் எல்லைக் கோட்டிற்குள் அமைந்த முழு சதுரங்களை எண்ணவும். இதனை, M எனக் கொள்க 

ஆ) பிறகு, பாதியளவு பரப்பிற்கு மேல் உள்ள சதுரங்களை எண்ணவும். இதனை, N எனக் கொள்க. 

இ) அடுத்து, பாதி அளவு பரப்புள்ள சதுரங்களை எண்ணவும். இதனை, P எனக் கொள்க. 

ஈ) இறுதியாக, பாதி அளவு பரப்பிற்குக் கீழ் உள்ள சதுரங்களை எண்ணவும்.  இதனை, Q எனக்  கொள்க

இப்போது, இலையின் பரப்பளவினை தோராயமாக பின்வரும் சூத்திரத்தின் மூலம் கண்டறியலாம்.

இலையின் தோராயமான பரப்பு = M +3/4  N+1/2 P + 1/4  Q சதுர செ.மீ

இலையின்பரப்பு = 51+ (¾) × 15 + (½) × 4 + (¼) × 11. செ.மீ2

= 51 + 11.25 + 2 + 2.75 = 67 சதுர செ.மீ. 

இந்தமுறையின் மூலம் எந்தவொரு ஒழுங்கற்ற பொருளின் பரப்பினையும் கணக்கிடலாம். மேலே விளக்கப்பட்ட வரைபட முறை மூலம், ஒழுங்கான வடிவமுள்ள பொருள்களின் பரப்பளவினையும் காணமுடியும். சதுர மற்றும் செவ்வக வடிவமுள்ள பொருள்களின் பரப்பளவினை இம்முறையில் துல்லியமாகக் காண முடியும்.

செயல்பாடு : 2

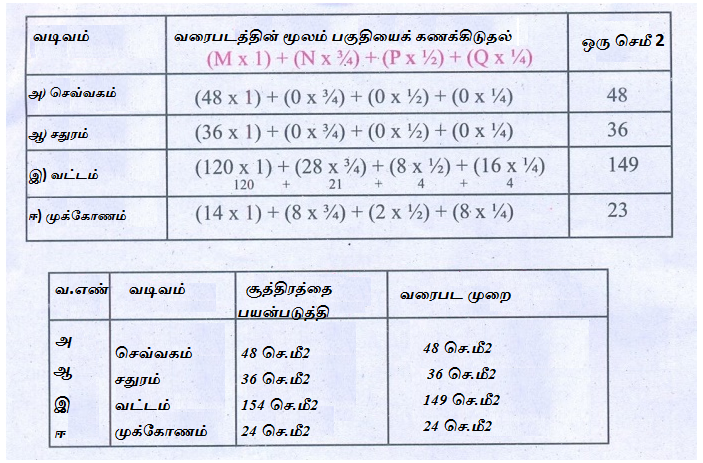
கீழே தரப்பட்டுள்ள ஒழுங்கான வடிவமுள்ள பொருள்களின் அளவுகளை, ஒரு வரைபடத் தாளின் மீது வரைந்து, அவற்றின் பரப்பளவினை வரைபட முறையில் காணவும். மேலும், அவற்றின் பரப்பளவினை தகுந்த சூத்திரத்தின் மூலமும் கண்டறியவும். இரு முறைகளிலும் கிடைத்த மதிப்புகளை அட்டவணைப்படுத்தி, அவற்றை ஒப்பிடவும் 

அ. 12 செ.மீ. நீளமும் 4 செ.மீ. அகலமும் கொண்ட செவ்வகம் 

ஆ. 6 செ.மீ. பக்க அளவுள்ள சதுரம் 

இ. 7 செ.மீ. ஆரம் கொண்ட வட்டம் 

ஈ. 6 செ.மீ. அடிப்பக்கமும் 8 செ.மீ. உயரமும் கொண்ட  முக்கோணம்

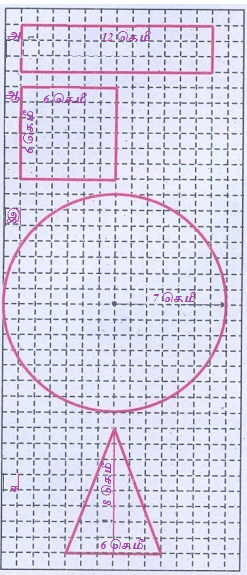
அ) A = a × b

         = 12 × 4 செ.மீ²

         = 48 செ.மீ2

M × 1 = 48 × 1 = 48 செ.மீ²

ஆ) A   = a × a    = 6 × 6 செ.மீ²

              = 36 செ.மீ2

M × 1 = 36 × 1 = 36 செ.மீ²

இ) A    = πr2

           = 22/7 × 7 × 7

           = 154 செ.மீ²

ஈ) A    = 1/2 ab = 1/2 × 6 × 8

           = 24 செ.மீ² 

ஒரு சதுர மீட்டர் என்பது ஒரு மீட்டர் பக்க அளவு கொண்ட சதுரம் ஒன்றினுள் அடைபடும் பரப்பாகும். பரப்பளவு என்பது சதுர மீட்டரில் குறிக்கப்பட்டாலும், பரப்பு சதுர வடிவமாக இருக்க வேண்டிய அவசியமில்லை.