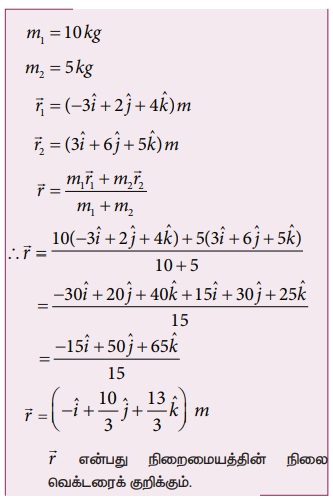இயற்பியல் - இருபுள்ளி நிறைகளின் நிறை மையம் | 11th Physics : UNIT 5 : Motion of System of Particles and Rigid Bodies
11வது இயற்பியல் : அலகு 5 : துகள்களாலான அமைப்பு மற்றும் திண்மப்பொருட்களின் இயக்கம்
இருபுள்ளி நிறைகளின் நிறை மையம்
இருபுள்ளி நிறைகளின் நிறை மையம்
நிறை மையத்திற்கான மேற்கண்ட சமன்பாட்டின் மூலம், x அச்சில் முறையே x1 மற்றும் x2 தொலைவில் அமைந்துள்ள m1, m2 என்ற இரண்டு புள்ளி நிறைகளின் நிறை மையத்தைக் கண்டறிவோம். இந்நேர்வில், ஆய அச்சு அமைப்பைப் பொருத்து நிறை மையத்தின் நிலையைக் கீழ்க்கண்ட மூன்று வழிகளில் காணலாம்.
(i) நிறைகள் நேர் X அச்சில் உள்ளபோது
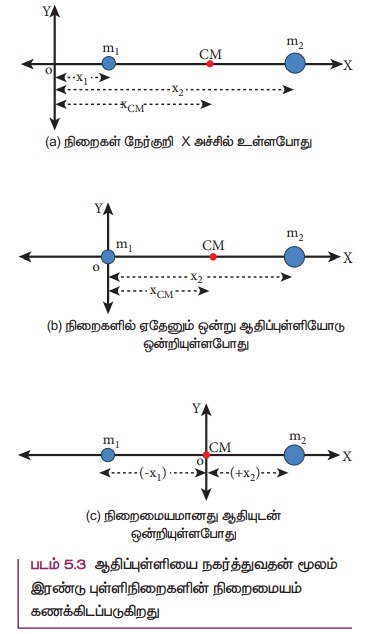
படம் 5.3 (a) இல் காட்டப்பட்டுள்ளதைப் போல m1, m2 என்ற நிறைகள் தன்னிச்சையாக எடுக்கப்பட்ட ஆதிப்புள்ளியைப் பொருத்து நேர் X அச்சில் முறையே x1 மற்றும் x2 நிலைகளில் உள்ளதாக எடுத்துக் கொள்வோம். நேர் X அச்சிலேயே xcm என்ற தொலைவில் அமைந்த நிறை மையத்தின் சமன்பாடானது
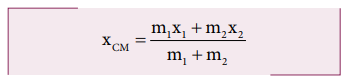
(ii) நிறைகளில் ஏதேனும் ஒன்று ஆதியுடன் ஒன்றியுள்ளபோது
படம் 5.3(b) இல் காட்டப்பட்டுள்ளவாறு ஏதேனும் ஒரு நிறை ஆய அச்சின் ஆதிப்புள்ளியோடு ஒன்றியுள்ள போது கணக்கீடானது இன்னும் எளிதாக்கப்படுகிறது. புள்ளி நிறை m1 ஆதிப்புள்ளியோடு ஒன்றும் போது, அதன் நிலை x1 சுழியாகிறது அதாவது, x1 = 0 எனவே,
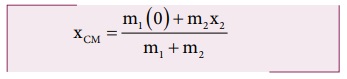
இதை மேலும் எளிதாக்கும் போது
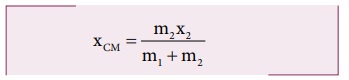
(iii) நிறைமையமானது ஆதியுடன் ஒன்றியுள்ளபோது
ஆய அச்சு அமைப்பின் ஆதிப்புள்ளியானது நிறை மையத்தோடு ஒன்றியுள்ள போது XCM = 0 மேலும் படம் 5.3 (c) இல் காட்டியுள்ளபடி நிறை m1 ன் நிலையானது எதிர்குறி X அச்சில் அமையும். எனவே இதன் நிலை எதிர்குறியாக இருக்கும்.
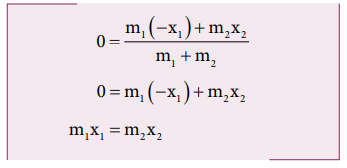
மேலே கொடுக்கப்பட்டுள்ள சமன்பாடு திருப்புதிறன்களின் தத்துவம் எனப்படுகிறது. இதைப்பற்றி பிரிவு 5.3.3 இல் விரிவாகப் பயிலலாம்.
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் இருபுள்ளி நிறைகளின் நிறை மையம்
எடுத்துக்காட்டு 5.1
3 kg, 5 kg என்ற இரு புள்ளி நிறைகள் X அச்சில் ஆதிப்புள்ளியிலிருந்து முறையே 4 m, 8 m என்ற தொலைவில் உள்ளன. இரு புள்ளி நிறைகளின் நிறை மையத்தின் நிலைகளை,
(i) ஆதிப்புள்ளியிலிருந்தும்
(ii) 3 kg நிறையிலிருந்தும் காண்க.
தீர்வு
m1 = 3 kg, m2 = 5 kg என எடுத்துக் கொள்வோம்.
(i) ஆதிப்புள்ளியிலிருந்து நிறை மையத்தைக் கண்டறிதல்
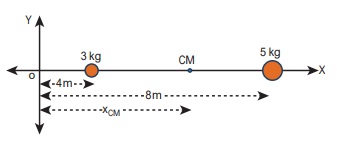
புள்ளி நிறைகள் X அச்சில் ஆதிப்புள்ளியிலிருந்து x1 = 4m, x2 = 8m என்ற தொலைவில் உள்ளன. எனவே நிறை மையம்.
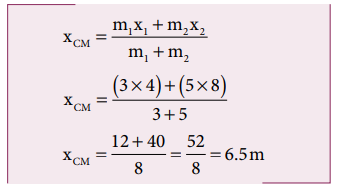
ஆதிப்புள்ளியிலிருந்து நிறை மையம் 6.5 m தொலைவில் அமைந்திருக்கும்.
(ii) 3 kg நிறையிலிருந்து நிறை மையத்தைக் கண்டறிதல்
3 kg நிறையை ஆதிப்புள்ளிக்கு X அச்சில் இடமாற்றம் செய்வதாக கொள்வோம். ஆதிப்புள்ளியானது X அச்சில் 3 kg நிறையுள்ள இடத்தில் எடுத்துக் கொள்ளப்படுகிறது. எனவே 3 kg புள்ளி நிறையின் நிலை சுழியாகும் (x1 = O) மாற்றப்பட்ட ஆதிப் புள்ளியிலிருந்து 5 kg நிறை 4 m தொலைவில் உள்ளது. (x2 = 4m)
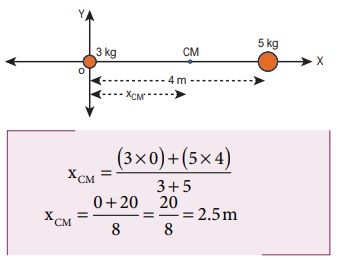
3 kg புள்ளி நிறையிலிருந்து 25 m தொலைவில் (5kg புள்ளி நிறையிலிருந்து 1.5 m தொலைவிலும்) நிறை மையம் அமைந்துள்ளது.
• இம்முடிவானது, நிறை மையம் அதிக நிறைக்கு அருகில் உள்ளதைக் காட்டுகிறது.
• ஆதிப்புள்ளி நிறைமையத்தில் அமையுமாறு கருதும்போது, திருப்புத் திறன்களின் தத்துவத்தை ஒத்து அமைகிறது.
m1 x1 = m2 x2; 3 × 2.5 = 5 × 1.5; 7.5 = 7.5
நிகழ்வு (i) யை (ii) உடன் ஒப்பிடும் போது 3 kg நிறையின் நிறைமையத்தினை 6.50 லிருந்து 4 m ஐக் கழிக்க Xcm = 25m எனவும் கண்டறியலாம் இது நிகழ்வு (i) இன் நிறைமையத்தின் நிலையிலேயே உள்ளது
எடுத்துக்காட்டு 5.2
R ஆரமுடைய சீரான பரப்பு நிறை அடர்த்தி கொண்ட வட்டத்தட்டிலிருந்து R/2 ஆரமுடைய ஒரு சிறு தட்டு வடிவப் பகுதி படத்தில் காட்டியுள்ளவாறு வெட்டி எடுக்கப்படுகிறது. மீதமுள்ள பகுதியின் நிறை மையத்தைக் கணக்கிடுக.
தீர்வு
வெட்டப்படாத வட்டத்தட்டின் நிறையானது M என எடுத்துக் கொள்க. இதனுடைய நிறை மையமானது வட்டத்தட்டின் வடிவியல் மையத்தில் அமையும். இப்புள்ளியிலேயே ஆதிப்புள்ளியும் ஒருங்கமைகிறது.
வெட்டி எடுக்கப்பட்ட சிறு வட்டத்தட்டின் நிறை m என்க. (அதன் நிறை மையம் ஆதிப்புள்ளிக்கு) வலது புறத்தில் R/2 என்ற தொலைவில் படத்தில் காட்டியுள்ளவாறு அமைந்திருக்கும்.
எனவே வட்டத்தட்டின் மீதமுள்ள பகுதியின் நிறை மையம் ஆதிப்புள்ளிக்கு இடது புறத்தில் X தொலைவில் உள்ளதாக எடுத்துக் கொள்வோம். திருப்புத்திறன்களின் தத்துவத்திலிருந்து, கீழ்கண்டவாறு எழுத முடியும்.
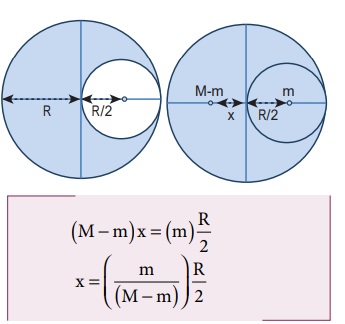
பரப்பு நிறை அடர்த்தி 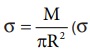 என்பது ஓரலகு பரப்பின் நிறை) எனில், சிறிய வட்டத் தட்டின் நிறை (m) என்பது
என்பது ஓரலகு பரப்பின் நிறை) எனில், சிறிய வட்டத் தட்டின் நிறை (m) என்பது

மீதமுள்ள வட்டத் தட்டின் நிறை மையமானது வட்டத் தட்டின் மையத்திற்கு இடப்புறம் R/6 என்ற தொலைவில் இருக்கும்.
• பெரிய வட்டத்தட்டிலிருந்து பொதுவான மையத்தை (common centre) பொருத்து சிறிய பகுதி வெட்டியெடுக்கப்பட்டால் மீதமுள்ள வட்டத்தட்டின் நிறை மையம் எங்கு அமையும்?
எடுத்துக்காட்டு 5.3
10 kg, 5 kg நிறையுடைய இரு புள்ளி நிறைகளின் நிலை வெக்டர்கள் முறையே 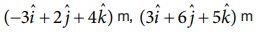 ஆகும். நிறை மையத்தின் நிலையைக் கண்டறியவும்.
ஆகும். நிறை மையத்தின் நிலையைக் கண்டறியவும்.
தீர்வு: