திண்மப் பொருட்களின் சமநிலை

திண்மப் பொருட்களின் சமநிலை (EQUILIBRIUM OF RIGID BODIES)

ஒரு பொருளானது மேசையின் மீது இயக்கமின்றி ஓய்வு நிலையில் உள்ளபோது பொருளின் மீது எந்த விசையும் செயல்படவில்லை என்கிறோம். உண்மையில் புவியீர்ப்பு விசையானது பொருளின் மீது கீழ்நோக்கியும் மேசையானது பொருளின் மீது ஏற்படுத்தும் எதிர்விசையானது மேல் நோக்கியும் அமைந்திருக்கும். இவ்விருவிசைகள் ஒன்றை ஒன்று சமன் செய்து கொள்கின்றன. எனவே, பொருளின் மீது நிகர விசை செயல்படவில்லை. பொருளின் மீது விசை செயல்படவில்லை என்பதற்கும், நிகர விசை செயல்பட வில்லை என்பதற்கும் அதிக வேறுபாடு உள்ளது. மேற்கூறிய விவாதமானது திருப்புத்திறன் அல்லது திருப்பு விசையின் அடிப்படையில் அமைந்த சுழற்சி இயங்கத்திற்கும் பொருந்தும். 

திண்மப் பொருளின் நேர்கோட்டு உந்தம் மற்றும் கோண உந்தம் மாறிலியாக இருந்தால் அப்பொருளானது எந்திரவியல் சமநிலையில் உள்ளது எனலாம். 

ஒரு பொருளின் நேர்க்கோட்டு உந்தம் மாறிலி எனில், அப்பொருளின் மீது செயல்படும் நிகரவிசை சுழியாகும்.

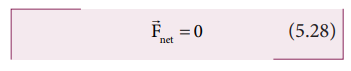
இந்நிபந்தனையின் படி பொருளானது இடப்பெயர்வில் சமநிலையில் உள்ளது. இதன்படி, பொருளின் மீது வெவ்வெறான திசைகளில் செயல்படும் 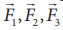   … என்ற விசைகளின் வெக்டர் கூடுதல் சுழியாகிறது.    

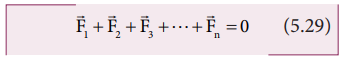
பொருளின் மீது 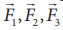 … என்ற விசைகள் வெவ்வேறான திசைகளில் செயல்படுகின்றன எனில் அவற்றின் விளைவை முறையே கிடைத்தள மற்றும் செங்குத்து கூறுகளின் மூலம் தீர்வு காணலாம். இந்நிகழ்வில் கிடைத்தளச் சமநிலைக்கோ செங்குத்துச் சமநிலைக்கோ சாத்தியம் உள்ளது. 

இதேபோல் கோண உந்தம் மாறிலியாக உள்ள போது பொருளின் மீதான நிகர திருப்பு விசை சுழியாகும்.

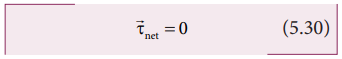
இந்நிபந்தனையின் படி பொருளானது சுழற்சி சமநிலையில் உள்ளது. சுழற்சிச் சமநிலையில் வெவ்வேறான சுழற்சியை உருவாக்கும் திருப்பு விசைகள் 1 , 2 , 3 … ஆகியவற்றின் வெக்டர் கூடுதல் சுழியாகிறது.

விசைகளும், திருப்பு விசைகளும் வெக்டர் அளவு என்பதால் இதன் திசைகளை தக்க குறியீடுகளுடன் பயன்படுத்த வேண்டும்.

சமநிலையின் வகைகள்

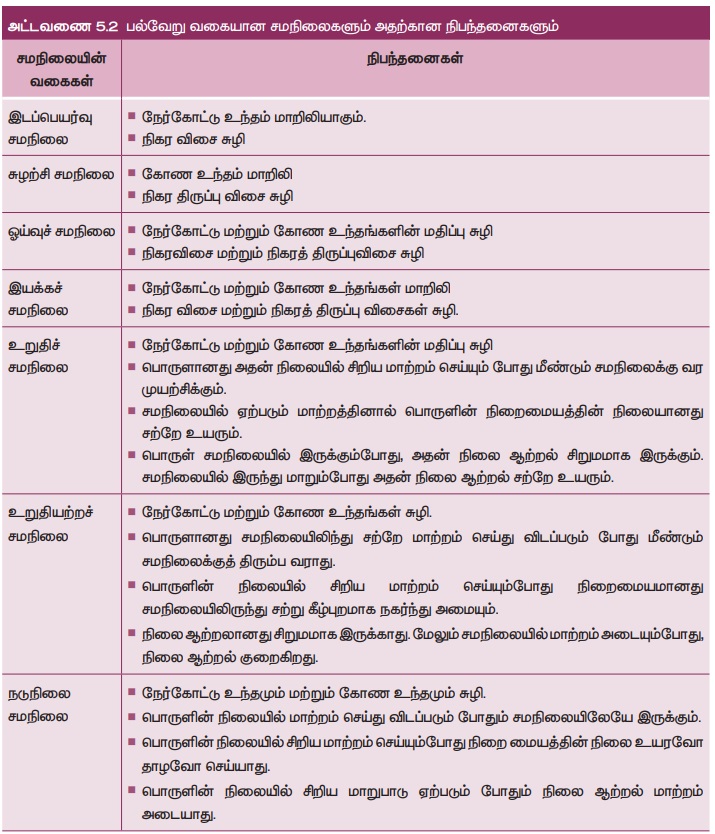
மேற்கண்ட விவாதத்தின்படி, வெவ்வேறான நிபந்தனைகளின் அடிப்படையில் வெவ்வேறு வகையான சமநிலைகளுக்கு வாய்ப்புள்ளது என்ற முடிவுக்கு வரலாம். இவை அட்டவணை 5.2 இல் தொகுக்கப்பட்டுள்ளன.

இரட்டை (Couple)

AB என்ற சீரான மெல்லியக் கம்பியை கருதுக, இதன் நிறைமையம் மையப்புள்ளி C யில் அமைந்து உள்ளது. கம்பியின் இரு முனைகள் A, B யில் சமமான எதிரெதிரான விசைகள் முறையே கம்பிக்கு செங்குத்தாக 2r இடைவெளியில் செயல்படுகிறது. படம் 5.13 இல் காட்டியுள்ளவாறு இவ்விரு விசைகளும் செயல்படுகிறது.

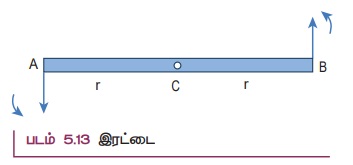
இரு சமமான விசைகள் எதிரெதிர் திசையில் செயல்பட்டு ஒன்றை ஒன்று சமன் செய்வதால் கம்பியின் மீதான நிகர விசை சுழியாகும். இப்பொழுது கம்பியானது இடப்பெயர்வு சமநிலையில் உள்ளது ஆனால் சுழற்சி சமநிலையில் இல்லை. எப்படி சுழற்சி சமநிலையில் இல்லை என்பதைக் காண்போம். கம்பியின் முனை A யில் செயல்படும் விசையின் திருப்புத்திறன் மையப்புள்ளி C யைப் பொருத்து எதிர் கடிகாரச் சுற்று (இடஞ்சுழி) திசையில் சுழற்சியை ஏற்படுத்தும். இதே போன்று கம்பியின் மறுமுனை B-ல் செயல்படும் விசையின் திருப்புத் திறனானது எதிர் கடிகாரச் சுற்று (இடஞ்சுழி) திசையிலே சுழற்சியை உருவாக்குகிறது. இவ்விரு விசையின் திருப்புத்திறன்களானது கம்பியின் மீது ஒரே மாதிரியான சுழற்சியை உணரச் செய்கிறது. எனவே, கம்பியானது இடப்பெயர்வு சமநிலையில் உள்ள போதும், சுழற்சி இயக்கத்திற்கு அல்லது திருப்பு விளைவிற்கு உள்ளாகிறது.

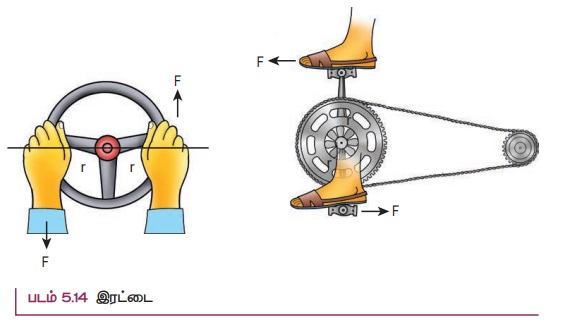
ஒரே நேர்கோட்டில் அமையாத, செங்குத்துத் தொலைவில் பிரிக்கப்பட்டுள்ள இரு சமமான எதிரெதிர் விசைகள் ஏற்படுத்தும் திருப்பு விளைவு இரட்டையின் திருப்புத்திறன் எனப்படும். அன்றாட வாழ்வில் நாம் காணும் பல செயல்களில் இரட்டையின் திருப்புத்திறனை படம் 5.14 இல் காணலாம்.

சில நிகழ்வுகளில் இவ்விரு விசைகள் ஒன்றையொன்று சமன் செய்யாது. இரு விசைகள் ஒத்த விசைகளாக இல்லாமல் எதிரெதிர் திசையில் இல்லாமலும் இருப்பின், பொருளானது நேர்கோட்டு இயக்கம் மற்றும் சுழற்சி இயக்கம் இரண்டையும் பெற்றிருக்கும்.

திருப்புத் திறன்களின் தத்துவம்

மெல்லிய, புறக்கணிக்கத்தக்க (negligible) நிறையுள்ள கம்பித் துண்டு, நீளத்தின் வழியாக சுழலியக்க மையத்தில் பொருத்தப்பட்டுள்ளது. மற்றும் F1 என்னும் F2 இரு விசைகளானது d1 மற்றும் d2 தொலைவுகளில் கம்பியின் முனைகளில் செயல்படுவது படம் 5.15 இல் காட்டப்பட்டுள்ளது. F1 மற்றும் F2 என்ற இரு விசைகள் தாங்கு மையத்திலிருந்து d1 மற்றும் d2 தொலைவுகளில் செயல்படுவதனால் படத்தில் காட்டியுள்ளவாறு செங்குத்து எதிர்வினை N நிறை சுழலியக்க மையத்தில் செயல்படுகிறது. கம்பியானது கிடைத்தள நிலையில் ஓய்வாக இருப்பதற்கு அது நேர்கோட்டு மற்றும் சுழற்சி சமநிலையில் இருக்க வேண்டும். எனவே, நிகர விசை மற்றும் நிகர திருப்பு விசை இரண்டும் சுழியாகும்.

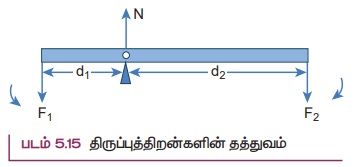
நேர்கோட்டு சமநிலையில், 

சுழலியக்க மையத்தை பற்றிய நிகர விசை சுழியாகும், -F1 + N – F2 = 0

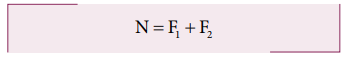
சுழற்சி சமநிலையில், 

சுழலியக்க மையத்தை பற்றிய நிகர திருப்புவிசை சுழியாகும், d1F1 - d2E2 = 0 

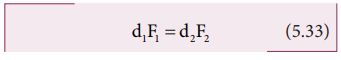
இத்தத்துவத்தைக் கொண்டு கோல் தராசானது, d1 = d2; F1 = F2 என்ற நிபந்தனையின் படி பொருட்களின் நிறையை அளவிடுகிறது. சமன்பாடு 5.33 யை மாற்றி அமைக்க. 

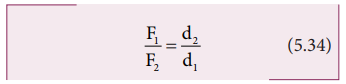
F1 பளு எனவும், F2 வை நமது முயற்சி எனவும் நேர்கோட்டு மற்றும் சுழற்சி சமநிலையில் இருக்க கருதினால், d1 < d2 என்ற நிபந்தனையில் நமக்கு அனுகூலமாக அமையும். இது F1 > F2 என்பதைக் குறிக்கிறது. எனவே, பெரிய பளுவைக் கூட சிறிய முயற்சியினால் உயர்த்த முடியும். தகவு (d2/d1) எளிய நெம்புகோலின் இயந்திரலாபம் எனப்படும். சுழலியக்க மையப்புள்ளியை ஆதாரப்புள்ளி என்றும் அழைக்கலாம்.

மேற்காணும் தத்துவத்தின் படி பல எளிய இயந்திரங்கள் இயங்குகின்றன.

ஈர்ப்பு மையம்

திண்மப் பொருட்கள் அனைத்தும் பல புள்ளி நிறைகளால் ஆக்கப்பட்டுள்ளது. புள்ளி நிறைகள் அனைத்தும் புவியின் மையத்தை நோக்கிய ஈர்ப்பியல் விசையினை உணர்கிறது. நடைமுறை வாழ்வில் எந்தவொரு திண்மப் பொருளின் அளவை விட புவி மிக பெரியதாக இருப்பதால் இவ்விசைகள் அனைத்தும் கீழ்நோக்கி இணையாக செயல்படுவதாக நாம் கருதலாம். இது படம் 5.16 இல் காட்டப்பட்டுள்ளது.

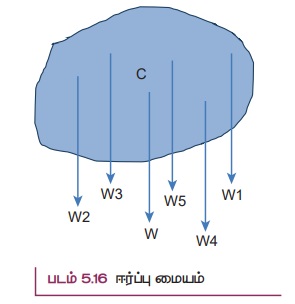
இந்த இணையான விசைகளின் தொகுபயன் விசை எப்பொழுதும் ஒரு புள்ளி வழியே செயல்படுகிறது. அப்புள்ளியே பொருளின் ஈர்ப்பு மையம் என்றழைக்கப்படுகிறது (புவியைப் பொருத்து). ஒரு பொருளின் நிலை மற்றும் திசையைக் கருதாத போது, அப்பொருளின் மொத்த எடையும் செயல்படுவதாகத் தோன்றும் புள்ளி அப்பொருளின் ஈர்ப்பு மையம் எனப்படும்.

சீரான புவியீர்ப்பு புலத்தில் ஒரு திண்மப்பொருளின் நிறைமையமும், ஈர்ப்பு மையமும் ஒரே புள்ளியில் அமையும். புவியீர்ப்பு புலத்தைப் பற்றி அலகு 6 இல் விளக்கப்பட்டுள்ளது. 

நாம் சீரான ஒழுங்கற்ற வடிவமுள்ள மெல்லிய தகட்டின் ஈர்ப்பு மையத்தைக் கூட வெவ்வேறான சுழலியக்க புள்ளிகளில் பொருத்திப்பார்த்து கண்டறியலாம்.

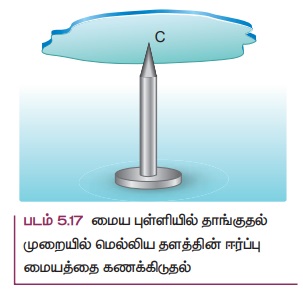
மெல்லிய பொருளானது கிடைக்கை நிலையில் இருக்கும் பொழுது, பொருளின் மொத்த எடையானது செயல்படும் புள்ளியான ஈர்ப்பு மையத்தில் சுழலியக்க புள்ளி அமைந்திருப்பதை படம் 5.17 இல் காணலாம். படம் 5.17ல் காட்டியுள்ளபடி நிகர ஈர்ப்பு விசைகள் செயல்படும் புள்ளியான ஈர்ப்பு மையத்தில், மெல்லிய பொருளானது நிலைநிறுத்தப்படும் போது கிடக்கையாகவே உள்ளது. 

பொருளானது ஈர்ப்பு மையத்தில் நிறுத்தப்பட்டுள்ள போது திண்மப் பொருளில் உள்ள எல்லா புள்ளி நிறைகளின் மீது செயல்படும் திருப்புவிசைகளின் தொகுபயன் சுழியாகும். மேலும் பொருளின் எடையானது சுழலியக்க புள்ளியில் செயல்படும் செங்குத்து விசையினால் சமன்செய்யப்படுகிறது. பொருளானது உறுதிச் சமநிலையில் கிடைக்கை நிலையிலேயே அமைந்திருக்கும். 

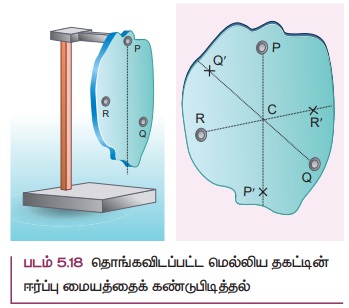
ஒழுங்கற்ற மெல்லிய பொருட்களின் ஈர்ப்பு மையத்தினை மற்றொரு முறையின் மூலமும் கண்டறியலாம். பொருளானது P, Q, R என்ற வெவ்வேறான புள்ளிகளில் படம் 5.18 இல் காட்டியுள்ளவாறு தொங்கவிடப்படுகிறது எனில், PP', QQ', RR' ஆகிய குத்துக் கோடுகள் அனைத்தும் ஈர்ப்பு மையம் வழியாக செல்கிறது. இங்கு பொருள் தொங்கவிடப்பட்ட புள்ளியில் செயல்படும் எதிர் விசையும் நிறைமையத்தின் மீது செயல்படும் புவியீர்ப்பு விசையும் ஒன்றை ஒன்று சமன் செய்கிறது. மேலும் இவற்றால் ஏற்படும் திருப்பு விசைகளும் குத்து கோடுகளின் மீது உள்ள போது ஒன்றை ஒன்று சமன் செய்கிறது.

வட்டப்பாதையில் மிதிவண்டி ஒட்டுபவரின் சாய்வு இயக்கம்

மிதிவண்டி ஓட்டுபவர் சமநிலையில் r ஆரம் உள்ள வட்டப்பாதையில் (உயர்த்தப்படாத பாதையில்) v வேகத்துடன் செல்ல முயற்சிப்பதாகக் கருதுவோம். மிதிவண்டி மற்றும் ஒட்டுபவரையும் சேர்த்து m நிறை கொண்ட ஒரே அமைப்பாகக் (simple system) கருதுவோம். இவ்வமைப்பின் நிறைமையம் C மற்றும் இது O வை மையமாக கொண்டு r ஆரம் கொண்ட வட்டப் பாதையில் செல்கிறது. படம் 5.19 இல் காட்டியுள்ளவாறு OC யை X அச்சாகவும், O- வழியே செல்லும் செங்குத்துக் கோடு OZ-ஐ Z-அச்சாகவும் கொள்வோம்.

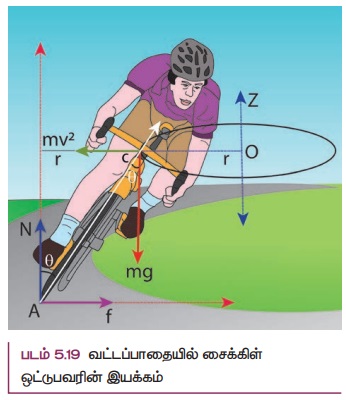
இவ்வமைப்பு (system) Z - அச்சை சுழல் அச்சாகக் கொண்டு, என்ற கோணத் திசைவேகத்தில் 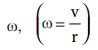Z அச்சைப் பொறுத்து சுழல்கிறது. இவ்வமைப்பானது சுழலும் குறிப்பாயத்தில் ஓய்வு நிலையில் உள்ளது. சுழலும் குறிப்பாயத்தைக் கொண்டு நாம் தீர்வுகளை காணும்போது அமைப்பின் மீது மையவிலக்கு விசை (போலி விசை) mv2/r செயல்படுவதாகக் கருதவேண்டும். இவ்விசையானது ஈர்ப்பு மையம் வழியாக செயல்படுகிறது. இவ்வமைப்பின் மீது செயல்படும் விசைகளாவன (i) புவியீர்ப்பு விசை mg (i) செங்குத்து விசை N (iii) உராய்வு விசை f மற்றும் (iv) மைய விலக்கு விசை (mv2/r). சுழற்சி குறிப்பாயத்தில் அவ்வமைப்பானது சமநிலையில் இருக்க வேண்டுமானால் அதன் மீது செயல்படும் நிகர விசை மற்றும் நிகர திருப்பு விசையின் மதிப்பு சுழியாக வேண்டும். A என்ற புள்ளியைப் பொருத்து அனைத்து திருப்பு விசைகளும் செயல்படுவதாகக் கருதுவோம். அனைத்து திருப்பு விசைகளும் படம் 5.20 இல் காட்டப்பட்டுள்ளது எனக் கருதுக.

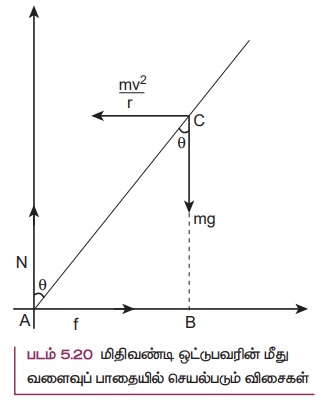
சுழற்சி சமநிலையில்

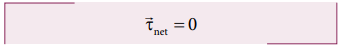
புள்ளி A வைப் பொருத்து, புவிஈர்ப்பு விசை mg ஆல் ஏற்படும் திருப்பு விசை = mg (AB) (கடிகார திசையில்)

மையநோக்கு விசையின் திருப்பு விசை

= mv2/r (BC) (எதிர் கடிகார திசையில்)

எதிர் கடிகார திசையை நேர்க்குறியாகவும், கடிகார திசையை எதிர்க்குறியாகவும் கொள்வது மரபு.

எனவே,

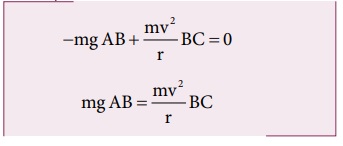
Δ ABC, AB = AC sinθ மற்றும் BC = AC cosθ

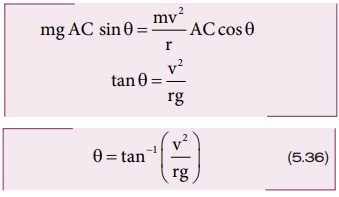
r ஆரம் கொண்ட சமமான வட்டப் பாதையில் v திசைவேகத்துடன் மிதிவண்டி ஒட்டுபவர் கடக்க முயற்சிக்கும்போது கீழே விழாமல் சமநிலையில் இருக்க θ கோணம் சாய்ந்த நிலையில் கடக்க வேண்டும்.

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் சமநிலையின் வகைகள்

எடுத்துக்காட்டு 5.12

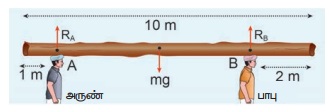
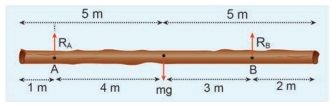
28 kg நிறையும் 10 m நீளமும் கொண்ட சீரான மரத்துண்டை அருண் மற்றும் பாபு சுமந்து செல்கின்றனர். மரத்துண்டின் முனைகளிலிருந்து இவர்கள் முறையே 1m மற்றும் 2m தொலைவில் பிடித்துள்ளனர். இவர்களில் யார் மரத்துண்டின் எடையை அதிகம் தாங்கிச் செல்கின்றார் [g=10ms-2]

தீர்வு 

மரத்துண்டானது இயந்திரவியல் சமநிலையில் உள்ளது எனக் கொள்க. அதன்படி மரத்துண்டின் மீது நிகர விசை மற்றும் நிகர திருப்பு விசையின் மதிப்பு சுழி. புவி ஈர்ப்பு விசையானது மரத்துண்டின் நிறைமையத்தில் கீழ் நோக்கி செயல்படும். அருண் மற்றும் பாபு முறையே A மற்றும் B புள்ளிகளில் செலுத்தும் RA, RB என்ற செங்குத்து விசைகள் கீழ்நோக்கிய புவியீர்ப்பு விசையை சமன் செய்கிறது. 

மரத்துண்டின் மொத்த எடை, W = mg = 28 × 10 = 280 N, ஆனது இருவராலும் தாங்கப்படுகிறது. மீள் செயல் விசையை இருவரும் தனித்தனியே அளிக்கின்றனர். மரத்துண்டின் மீது செயல்படும் அனைத்து விசைகளையும் தனித்த பொருளின் விசைப்படம் மூலம் காணலாம்.

இடப்பெயர்வு சமநிலையின் படி:

மரத்துண்டின் மீது செயல்படும் நிகர விசை சுழியாகிறது

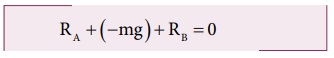
இங்கு, RA மற்றும் RB விசைகள் மேல் நோக்கிய நேர் குறியிலும். ஈர்ப்பியல் ஈர்ப்பு விசை (அல்லது எடை) கீழ்நோக்கி எதிர்குறியிலும் செயல்படுகிறது. 

RA + RB = mg 

சுழற்சி சமநிலையின் படி:

மரத்துண்டின் மீது செயல்படும் நிகர திருப்பு விசையின் மதிப்பு சுழியாகிறது. விசைகள் தொலைவிற்கு செங்குத்து என்பதால்,

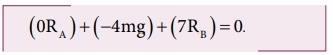
இங்கு, எதிர்வினை RA ஆனது தாங்கும் புள்ளி A யிலேயே செயல்படுவதால் A யைப் பொருத்து RA யின் திருப்புவிசை சுழியாகும். ஆனால் எடை mg யானது A யைப் பொருத்து கடிகார திசையிலும், எதிர்வினை RB ஆனது A யைப் பொருத்து எதிர் கடிகார திசையிலும் திருப்பு விசைகளை ஏற்படுத்தும்.

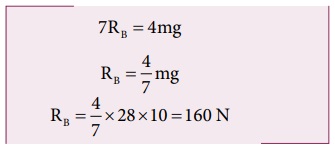
RB யின் மதிப்பை பிரதியிட, 

RA = mg - RB 

RA = 28 × 10 - 160 = 280 - 160 = 120 N 

RB ஆனது RA ஐ விட அதிகமாக இருப்பதால், பாபு அருணைவிட அதிக எடையை சுமக்கிறார்.

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் வட்டப்பாதையில் மிதிவண்டி ஒட்டுபவரின் சாய்வு இயக்கம்

எடுத்துக்காட்டு 5.13

20ms-1 என்ற திசைவேகத்துடன் வட்டப்பாதையில் மிதிவண்டி ஒட்டுபவர் செங்குத்து தளத்துடன் 30° கோணம் சாய்ந்த நிலையில் கடக்கிறார். வட்டப்பாதையின் ஆரம் என்ன? 

(g = 10 ms-2 எனக் கொள்க) 

தீர்வு: 

மிதிவண்டி ஒட்டுபவரின் திசை வேகம், v = 20 ms-1 

குத்தச்சுடன் கோணம் θ = 30° 

வட்டப்பாதையைக் கடக்க நிபந்தனை 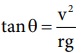மேற்கண்ட சமன்பாட்டை மாற்றி அமைக்க ஆரம் 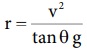ஐ பிரதியிட,