11வது இயற்பியல் : அலகு 5 : துகள்களாலான அமைப்பு மற்றும் திண்மப்பொருட்களின் இயக்கம்
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள்: நிறை மையம்
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் இருபுள்ளி நிறைகளின் நிறை மையம்
எடுத்துக்காட்டு 5.1
3 kg, 5 kg என்ற இரு புள்ளி நிறைகள் X அச்சில் ஆதிப்புள்ளியிலிருந்து முறையே 4 m, 8 m என்ற தொலைவில் உள்ளன. இரு புள்ளி நிறைகளின் நிறை மையத்தின் நிலைகளை,
(i) ஆதிப்புள்ளியிலிருந்தும்
(ii) 3 kg நிறையிலிருந்தும் காண்க.
தீர்வு
m1 = 3 kg, m2 = 5 kg என எடுத்துக் கொள்வோம்.
(i) ஆதிப்புள்ளியிலிருந்து நிறை மையத்தைக் கண்டறிதல்
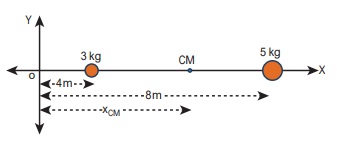
புள்ளி நிறைகள் X அச்சில் ஆதிப்புள்ளியிலிருந்து x1 = 4m, x2 = 8m என்ற தொலைவில் உள்ளன. எனவே நிறை மையம்.
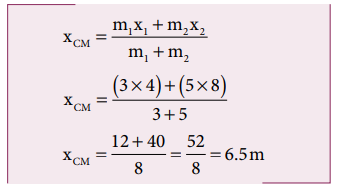
ஆதிப்புள்ளியிலிருந்து நிறை மையம் 6.5 m தொலைவில் அமைந்திருக்கும்.
(ii) 3 kg நிறையிலிருந்து நிறை மையத்தைக் கண்டறிதல்
3 kg நிறையை ஆதிப்புள்ளிக்கு X அச்சில் இடமாற்றம் செய்வதாக கொள்வோம். ஆதிப்புள்ளியானது X அச்சில் 3 kg நிறையுள்ள இடத்தில் எடுத்துக் கொள்ளப்படுகிறது. எனவே 3 kg புள்ளி நிறையின் நிலை சுழியாகும் (x1 = O) மாற்றப்பட்ட ஆதிப் புள்ளியிலிருந்து 5 kg நிறை 4 m தொலைவில் உள்ளது. (x2 = 4m)
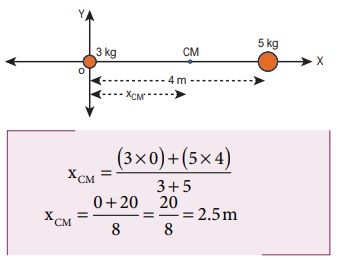
3 kg புள்ளி நிறையிலிருந்து 25 m தொலைவில் (5kg புள்ளி நிறையிலிருந்து 1.5 m தொலைவிலும்) நிறை மையம் அமைந்துள்ளது.
• இம்முடிவானது, நிறை மையம் அதிக நிறைக்கு அருகில் உள்ளதைக் காட்டுகிறது.
• ஆதிப்புள்ளி நிறைமையத்தில் அமையுமாறு கருதும்போது, திருப்புத் திறன்களின் தத்துவத்தை ஒத்து அமைகிறது.
m1 x1 = m2 x2; 3 × 2.5 = 5 × 1.5; 7.5 = 7.5
நிகழ்வு (i) யை (ii) உடன் ஒப்பிடும் போது 3 kg நிறையின் நிறைமையத்தினை 6.50 லிருந்து 4 m ஐக் கழிக்க Xcm = 25m எனவும் கண்டறியலாம் இது நிகழ்வு (i) இன் நிறைமையத்தின் நிலையிலேயே உள்ளது
எடுத்துக்காட்டு 5.2
R ஆரமுடைய சீரான பரப்பு நிறை அடர்த்தி கொண்ட வட்டத்தட்டிலிருந்து R/2 ஆரமுடைய ஒரு சிறு தட்டு வடிவப் பகுதி படத்தில் காட்டியுள்ளவாறு வெட்டி எடுக்கப்படுகிறது. மீதமுள்ள பகுதியின் நிறை மையத்தைக் கணக்கிடுக.
தீர்வு
வெட்டப்படாத வட்டத்தட்டின் நிறையானது M என எடுத்துக் கொள்க. இதனுடைய நிறை மையமானது வட்டத்தட்டின் வடிவியல் மையத்தில் அமையும். இப்புள்ளியிலேயே ஆதிப்புள்ளியும் ஒருங்கமைகிறது.
வெட்டி எடுக்கப்பட்ட சிறு வட்டத்தட்டின் நிறை m என்க. (அதன் நிறை மையம் ஆதிப்புள்ளிக்கு) வலது புறத்தில் R/2 என்ற தொலைவில் படத்தில் காட்டியுள்ளவாறு அமைந்திருக்கும்.
எனவே வட்டத்தட்டின் மீதமுள்ள பகுதியின் நிறை மையம் ஆதிப்புள்ளிக்கு இடது புறத்தில் X தொலைவில் உள்ளதாக எடுத்துக் கொள்வோம். திருப்புத்திறன்களின் தத்துவத்திலிருந்து, கீழ்கண்டவாறு எழுத முடியும்.
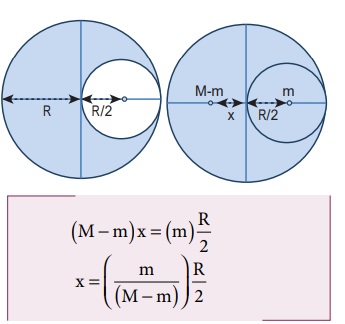
பரப்பு நிறை அடர்த்தி 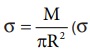 என்பது ஓரலகு பரப்பின் நிறை) எனில், சிறிய வட்டத் தட்டின் நிறை (m) என்பது
என்பது ஓரலகு பரப்பின் நிறை) எனில், சிறிய வட்டத் தட்டின் நிறை (m) என்பது

மீதமுள்ள வட்டத் தட்டின் நிறை மையமானது வட்டத் தட்டின் மையத்திற்கு இடப்புறம் R/6 என்ற தொலைவில் இருக்கும்.
• பெரிய வட்டத்தட்டிலிருந்து பொதுவான மையத்தை (common centre) பொருத்து சிறிய பகுதி வெட்டியெடுக்கப்பட்டால் மீதமுள்ள வட்டத்தட்டின் நிறை மையம் எங்கு அமையும்?
எடுத்துக்காட்டு 5.3
10 kg, 5 kg நிறையுடைய இரு புள்ளி நிறைகளின் நிலை வெக்டர்கள் முறையே 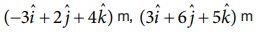 ஆகும். நிறை மையத்தின் நிலையைக் கண்டறியவும்.
ஆகும். நிறை மையத்தின் நிலையைக் கண்டறியவும்.
தீர்வு:
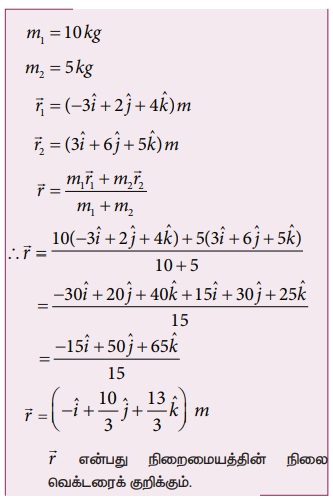
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் சீராகப் பரவியுள்ள நிறையின் நிறை மையம்
எடுத்துக்காட்டு 5.4
M நிறையும் l நீளமும் கொண்ட சீரான நீள் அடர்த்தி கொண்ட (uniform rod) தண்டின் நிறை மையத்தைக் கண்க.
தீர்வு
M நிறையும் l நீளமும் உடைய ஒரு சீரான நீள் அடர்த்தி கொண்ட தண்டினைக் (uniform rod) கருதுக. அதன் ஒரு முனை படத்தில் காட்டியுள்ள படி ஆதிப்புள்ளியுடன் ஒன்றியிருப்பதாக எடுத்துக்கொள்வோம். தண்டானது X அச்சில் வைக்கப்பட்டுள்ளது. தண்டினுடைய நிறை மையத்தைக் கண்டறிய, ஆதிப்புள்ளியிலிருந்து x தொலைவில் dx நீளமும் dm என்ற மீநுண் நிறையும் கொண்ட சிறுபகுதியை எடுத்துக் கொள்வோம்.
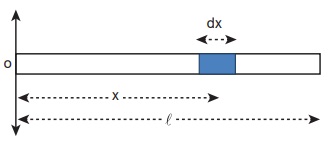
தண்டின் நீள் அடர்த்தி (ஓரலகு நீளத்திற்கான நிறை) 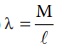
சிறிய பகுதியின் நிறை 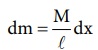 தண்டின் நிறை மையத்திற்கான சமன்பாட்டை கீழ்க்கண்டவாறு எழுதலாம்.
தண்டின் நிறை மையத்திற்கான சமன்பாட்டை கீழ்க்கண்டவாறு எழுதலாம்.

நிலை l/2 என்பது தண்டின் வடிவியல் மையமாகும். இதிலிருந்து சீரான தண்டினைப் பொறுத்தவரை அதன் வடிவியல் மையத்திலேயே (Geometric centre) நிறை மையம் அமையும் என்ற முடிவிற்கு வரலாம்.
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் நிறை மையத்தின் இயக்கம்
எடுத்துக்காட்டு 5.5
50 kg நிறையுள்ள ஒரு மனிதர் நிலையான நீரின் பரப்பில் மிதந்து கொண்டிருக்கும் 300 kg நிறையுடைய படகில் ஒரு முனையில் நின்று கொண்டிருக்கிறார். அவர் தரையில் நிலையாக உள்ள ஒருவரை பொருத்து படகின் மறுமுனையை நோக்கி 2ms-1 என்ற மாறாதிசைவேகத்தில் நடந்து செல்கிறார். (a) நிலையான உற்றுநோக்குபவரை பொருத்தும் (b) படகில் நடந்து கொண்டிருக்கும் மனிதரைப் பொருத்தும் படகின் திசைவேகம் என்ன?
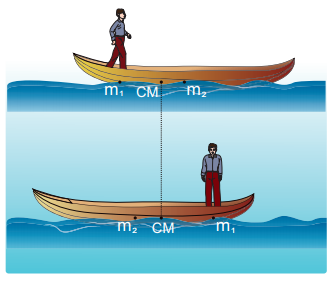
தகவல்: படகுக்கும் மனிதருக்கும் இடையே உராய்வு உள்ளது. ஆனால் படகுக்கும் நீருக்கும் இடையே உராய்வு கிடையாது.)
தீர்வு
மனிதரின் நிறை m1 = 50 kg
படகின் நிறை m2 = 300 kg
நிலையான உற்றுநோக்குபவரைப் பொருத்து:
மனிதர் நகரும் திசைவேகம் v1 = 2 ms-1 மேலும் படகு நகரும் திசைவேகம் v2 (கண்டறியப்பட வேண்டியது) என்க.
(i) தரையில் நிலையாக உள்ள உற்றுநோக்குபவரைப் பொருத்து படகின் திசைவேகத்தைக் கணக்கிடுதல்
அமைப்பின் மீது புறவிசைகள் செயல்படாதபோது, படகு - மனித அமைப்பின் அகவிசையாக செயல்படும் உராய்வின் காரணமாக மனிதன் - படகு அமைப்பு (boat - man system) இயங்குகிறது. ஆகவேநிறைமையத்தின் திசைவேகம் சுழியாகும் (vCM = 0).
நிறை மையத்தின் சமன்பாடு (5.7) லிருந்து,
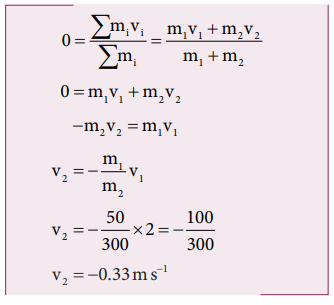
இங்கே, நிலையாக உள்ள உற்றுநோக்குபவருக்கு எதிர் திசையில் படகு செல்வதை எதிர்குறி காட்டுகிறது.
(ii) நடக்கும் மனிதரைப் பொருத்து படகின் திசைவேகத்தைக் கண்டறிதல்: படகின் சார்புத் திசைவேகத்தை பின்வருமாறு கணக்கிடலாம்.
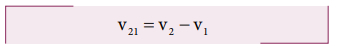
இங்கே, v21 என்பது நடக்கும் மனிதரைப் பொருத்து படகின் சார்புத் திசைவேகமாகும்
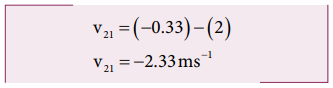
மனிதர் தன்னுடைய வலப்புறம் நகரும்போது படகு அவரின் இடது புறமாக நகர்வதை விடையில் உள்ள எதிர்குறி காட்டுகிறது.
• நடக்கும் மனிதனைப்பொருத்து படகின் சார்புத் திசைவேகத்தின் எண்மதிப்பானது, நிலையாக உற்று நோக்குபவரைப் பொருத்து படகின் சார்புத் திசைவேகத்தின் எண்மதிப்பை விட அதிகம்.
• நிலையாக உற்று நோக்குபவருக்கும் படகில் நடந்து செல்பவருக்கும் எதிர்திசையில் படகு இயங்குவதால் இரு விடைகளும் எதிர்குறியில் உள்ளன.
வெடித்தலின் நிறை மையம்
ஓய்வு நிலையிலோ அல்லது சீரான இயக்கத்திலோ உள்ள பொருளின் அகவிசைகளினால் (internal forces) வெடித்தல் நடைபெறுகிறது எனில், அதன் நிறை மையத்தின் நிலை பாதிக்கப்படுவதில்லை. அது, அதே ஓய்வு நிலையிலோ அல்லது சீரான திசைவேகத்திலோ இருக்கும். ஆனால் வெடித்தபகுதிகளின் இயக்கவியல் அளவுகள் (kinematic quantities) பாதிக்கப்படும். வெடித்தலானது புறவிசைகளின் காரணமாக நிகழ்கிறது எனில் நிறைமையம், மற்றும் வெடித்த பகுதிகள் ஆகியவற்றின் இயக்கவியல் அளவுகள் பாதிக்கப்படும்.
எடுத்துக்காட்டு 5.6
5 kg நிறையுள்ள எறியமானது, (projectile) அது இயக்கத்தில் உள்ள போதே தானாக வெடித்து இரு கூறுகளாகப் பிரிகிறது. அதில் 3 kg நிறையுடைய ஒரு கூறானது, வீச்சின் நான்கில் மூன்று பங்கு 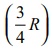 தொலைவில் விழுகிறது. மற்றொரு கூறு எங்கு விழும்?
தொலைவில் விழுகிறது. மற்றொரு கூறு எங்கு விழும்?
தீர்வு
புறவிசைகளின் துணையின்றி தானாக வெடிப்பதால் எறியத்தின் நிறை மையம் பாதிக்கப்படாது. மேலும் நிறைமையமானது தொடர்ந்து பரவளையப் பாதையிலேயே செல்லும். ஆனால் அதன் கூறுகளானது பரவளையப் பாதையை மேற்கொள்ளாது. கூறுகள் அனைத்தும் தரையில் விழும்போது நிறைமையம் எறியப்பட்ட புள்ளியிலிருந்து படத்தில் காட்டப்பட்டதுபோல் R தொலைவை (நெடுக்கம்) அடைகிறது. ஆகவே இறுதியில், படத்தில் காட்டியுள்ளபடி நிறை மையமானது எறி புள்ளியிலிருந்து R தொலைவில் (நெடுக்கம்) அமைந்திருக்கும்.
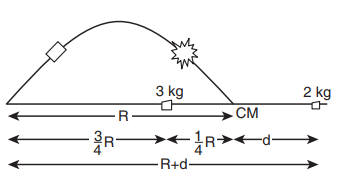
நிறைமையத்தின் இறுதி நிலையை ஆதி புள்ளியாக எடுத்துக் கொண்டால், திருப்புத்திறன்களின் தத்துவத்தின் படி
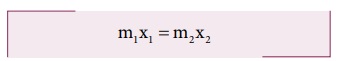
இங்கு, m1 = 3 kg, m2 = 2 kg, x1 = 1/4 R மற்றும் x2 = d என எடுத்துக் கொள்க.
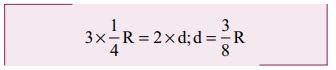
எறி புள்ளிக்கும் 2kg நிறை விழுந்துள்ள புள்ளிக்கும் இடையேயுள்ள தொலைவு R+d.
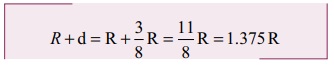
எனவே 2 kg நிறையுடைய மற்றொரு கூறானது எறிபுள்ளியிலிருந்து 1.375 R என்ற தொலைவில் விழுகிறது. (இங்கு R என்பது எறிபொருளின் கிடைத்தள நெடுக்கமாகும்)