வரையறுத் தொகையீட்டை ஒரு கூட்டலின் எல்லையாக காணல்(Definite Integral as the Limit of a Sum)

வரையறுத் தொகையீட்டை ஒரு கூட்டலின் எல்லையாக காணல்(Definite Integral as the Limit of a Sum) 

ரீமன் தொகையீடு (Riemann Integral)

[a, b], a < b எனும் மூடிய வரம்புக்குட்பட்ட இடைவெளியில் வரையறுக்கப்படும் ஒரு மெய் மதிப்புடைய சார்பு f (x) என்க. [a, b] இடைவெளியில் f (x) சார்பானது ஒரே குறியிடன் இருக்க வேண்டியதில்லை; அதாவது [a,b] -ல் f (x) -ன் மதிப்புகள் மிகையெண்ணாகவோ அல்லது  குறையெண்ணாகவோ இருக்கலாம். படம் 9.2 இல் காண்க. [a,b] எனும் இடைவெளியை n உள் இடைவெளிகளாக, a = x0 < x1 < x2 < …< xn-1 < xn = b எனுமாறு [x0, x1], [x1 , x2), …,[xn-2,xn-1),[xn-1 ,xn ] எனப் பிரிக்கவும்.

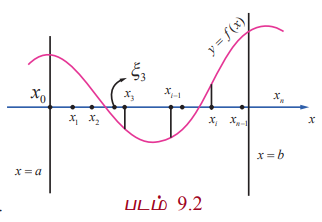
ஏதேனும் ஒரு மெய்யெண், ξi xi-1 ≤ ξi ≤ xi எனும்படி, [xi-1 xi], i = 1,2,…..n என்றியிருக்குமாறு தேர்ந்தெடுக்கவும். இதன் கூடுதல்,

∑ni=1 f (ξi )( xi − xi −1 ) = f (ξ1 )(x1 − x0 ) + f (ξ2 )(x2 − x1 ) + … + f (ξn )(xn − xn−1 ) ….(1) 

என எடுத்து கொள்க. கூடுதல் (1) என்பது [a,b]-ல் [x0,x1 ], [x1,x2 ], …, [xn-1,x1 ]எனும் பிரிவுகளில் f (x) என்பது ரீமன் கூட்டல் எனப்படும்.

xi −1 ≤ ξi ≤ xi எனும் நிபந்தனையை பூர்த்தி செய்யமாறு எண்ணற்ற பல ξi மதிப்புகள் இருப்பதால், [a,b]-ல் [x0,x1] , [x1,x2],…[xn-1 , xn] எனும் அதே பிரிவினைகளுடைய f (x)-க்கு எண்ணற்ற பல ரீமன் கூடுதல் உண்டு. கட்டுப்படுத்தும் செயல்பாட்டின் கீழ் n →∞ மற்றும் max (xi -xi-1) → 0 எனில், கூட்டுத் தொகை (1) ஆனது, முடிவுறு மதிப்பினை அதாவது A என வைத்துக் கொண்டால், மதிப்பு A -யினை [a,b]-ல் x-ஐப் பொருத்து f (x) -ன் ரீமன் தொகையீடு என்பர். மேலும் a-லிருந்து b -க்கு x -ஐப் பொருத்து b∫a f (x)dx எனக் குறிப்பிடப்படுகிறது. a = b எனில் a∫a f (x)dx = 0 ஆகும்.

குறிப்புரை

இந்த அத்தியாயத்தில் [a,b] -ல் தொடர்ச்சியான வரம்புக்குட்பட்ட f (x) -இன் சார்புகளை மட்டுமே கருத்தில் கொள்கிறோம். இருப்பினும், துண்டுவாரி தொடர்ச்சியான வரம்புக்குட்பட்ட சார்புகளுக்கும் [a, b] -ல் f (x) -ன் ரீமன் தொகையீடு உள்ளதாகும். வரையறுத்த தொகையீட்டிற்கும் எதிர்மறை வகையிடலுக்கும் (வரையறா தொகையீடு) ஒரே குறியீடான ∫ பயன்படுத்தப்படுகிறது. தொகையீடுக்கான அடிப்படைத் தேற்றத்தை நிறுவிய பிறகே இதன் காரணம் தெளிவாக விளங்கும். மாறிலி x போலியெனும் அர்த்தம் தரும்படி நம் விருப்பப்படி தேர்ந்தெடுக்கப்படுகிறது. எனவே b∫a f(x)dx என்பதனை b∫a f (u)du எனவும் எழுதலாம். ஆகையால், b∫a f(x)dx: =b∫a f (u)du ஆகும். [xi-1,xi], i =1,2,… ,n எனும் ஒவ்வொரு பகுதி இடைவெளியிலும் உள்ள xi-1, ξi , மற்றும் xi, ஆகிய மூன்று புள்ளிகளும் max (xi – xi-1) →0 என்பதால் ஒரே புள்ளியில் குவிகின்றன. ξi = xi-1, i =1,2,… ,n எனத் தேர்ந்தெடுப்பதன் மூலம்

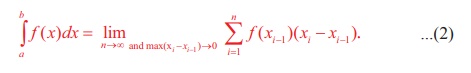
ஆகும். சமன்பாடு (2) ரீமன் தொகையீட்டினை மதிப்பிடுவதற்கான இடது-முனை விதி என்பர். ξi = xi , i=1,2,…,n எனத் தேர்ந்தெடுப்பதன் மூலம்,

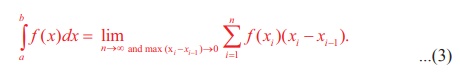
எனக் கிடைக்கிறது. சமன்பாடு (3)-ஐ ரீமன் தொகையீட்டினை மதிப்பிடுவதற்கான வலது-முனை விதி என்பர். 

ξi = xi-1 + xi / 2  i = 1,2,…,n எனத் தேர்ந்தெடுப்பதன் மூலம்

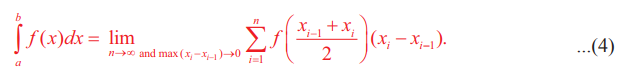
எனக் கிடைக்கிறது. சமன்பாடு (4) ரீமன் தொகையீட்டினை மதிப்பிடுவதற்கான நடு-முனை விதி என்பர்.

குறிப்புரை

(1) ஒவ்வொரு x∈ [a,b]-க்கும் ரீமன் தொகையீடு b∫a f(x)dx உள்ளது எனில், ரீமன் தொகையீடு x∫a f (u)du என்பது நன்கு வரையறுக்கப்பட்ட மெய்யெண்ணாகும். எனவே F(x) =x∫a f(u)du,x∈[a, b] எனும்படி [a,b]-ல் F(x)-இன் சார்பு வரையறுக்கப்படுகிறது.

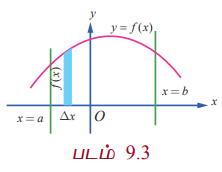
(2) அனைத்து x ∈ [a,b]-க்கும் f (x) ≥ 0 எனில்,ரீமன்தொகையீடானb∫a f (x)dx என்பது x = a மற்றும் x = b கோடுகள், y = f (x)எனும் வளைவரை மற்றும் x-அச்சின் வரம்பிற்குட்பட்ட பகுதியின் வடிவியல் பரப்பளவைத் தரும். படம் 9.3 இல் காண்க.

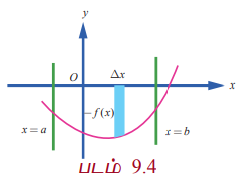
(3) அனைத்து x ∈[a,b] -க்கும் f (x) ≤ 0 எனில் ரீமன் தொகையீடான b∫a f(x) dx என்பது x = a மற்றும் x = b கோடுகள் y = f (x) எனும் வளைவரை மற்றும் x- அச்சின்வரம்பிற்குட்பட்ட பகுதியில் வடிவியல் பரப்பளவு குறை மதிப்பைத் தரும். படம் 9.4 இல் காண்க. இத்தகையதருணத்தில், x = a மற்றும் x = b கோடுகள், y = f (x) எனும் வளைவரை மற்றும் x-அச்சின்வரம்பிற்குட்பட்ட பகுதியின் வடிவியல் பரப்பளவு | b∫a f(x)dx) | ஆகும்.

(4) [a,b]-ல் f (x) மிகை மதிப்புகளையும் அதே சமயத்தில் குறை மதிப்புகளையும் பெறுமஎனில், [a,b] எனும் இடைவெளியை f (x) -இன், ஒவ்வொரு உள் இடைவெளியிலும் தொடர்ந்து ஒரே குறியுடன் இருக்குமாறு [a,c1], [c1,c2],…, ,[ck b] எனப் பகுதி இடைவெளிகளாகப் பிரிக்கப்படுகிறது. எனவே, b∫a f(x)dx - க்கான ரீமன் தொகையீடு

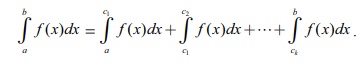 ஆகும் 

இத்தருணத்தில் x = a மற்றும் x = b கோடுகள், y = f (x) எனும் வளைவரை மற்றும் x-அச்சின் வரம்பிற்குட்பட்ட பகுதியின் வடிவியல் பரப்பளவு

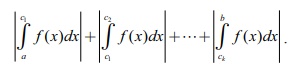ஆகும்

சான்றாக, சார்பு f (x), x ∈ [a, b] -க்கான கீழ்க்காணும் வளைவரையைக் கருதுவோம். படம் 9.5 இல் காண்க. இங்கு, A1, A2 மற்றும் A3 ஆகியவை தனித்தனியான வடிவியல் பரப்பளவுகளாகும். எனவே வரையறுத்த தொகையீடு b∫a f (x)dx என்பது

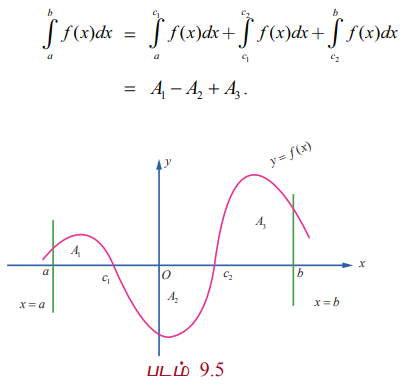
        = A1 – A2 + A3

x = a மற்றும் x = b கோடுகள், y = f (x) எனும் வளைவரை மற்றும் x – அச்சின் வரம்பிற்குட்பட்ட பகுதியின் வடிவியல் பரப்பளவு A1 + A2 + A3 ஆகும். மேற்கண்ட ஆய்விலிருந்து, வடிவியல் பரப்பளவை ரீமன் தொகையீடு குறிக்காது என்பது புலனாகிறது.

குறிப்பு

வெளிப்படையாக குறிப்பிடாமல் இருப்பினும் பரப்பளவு சதுர அலகுகளாகவும், கன அளவு கன அலகுகளாகவும் கணக்கிடப்படுகின்றது என்பது நன்கு தெளிவாகிறது. 

எடுத்துக்காட்டு 9.1

5 சம அளவு பகுதி இடைவெளிகளாகப் பிரித்து மற்றும் (ii) இடது-முனை விதி (i) வலது-முனை விதி (i) நடு-முனை விதி ஆகியவற்றை ரீமன் கூட்டலில் பயன்படுத்தி 0.5∫0 x2 dx ன் மதிப்பைக் கணக்கிடுக. 

தீர்வு

இங்கு a = 0, b = 0.5,n = 5, f (x) = x2 எனவே, ஒவ்வொரு பகுதி இடைவெளியின் அகலம்,

h = ∆x = b-a / n = 0.5 - 0 / 5 = 0.1 ஆகும்.

இடைவெளியின் துண்டுகளைத் தரும் புள்ளிகள்,

x0 = 0,

x1= x0 + h = 0 + 0.1 = 0.1

x2 = x1 + h = 0.1 + 0.1 = 0.2

x3 = x2 + h = 0.2 + 0.1 = 0.3

x4 = x3 + h = 0.3 + 0.1 = 0.4

x5 = x4 + h = 0.4 + 0.1 = 0.5 ஆகும்.

(i) சம அளவு∆x கொண்ட ரீமன் கூட்டலுக்கான இடது முனை விதியானது,

S = [f (x0)+ f (x1) +...+ f (xn-1)]∆x. 

ஃS = [f (0) + f (0.1) + f (0.2) + f (0.3) + f (0.4)] (0.1)

= [0.00+0.01+0.04+0.09+0.16](0.1) = 0.03 

∫0.50 x2dx -ன் தோராய மதிப்பு 0.03 ஆகும்.

(ii) சம அளவு ∆x கொண்ட ரீமன் கூட்டலுக்கான வலது முனை விதியானது

S = [f (x1) + f (x2)+---+ f (xn)]∆x. 

ஃ S = [f (0.1) + f (0.2) + f (0.3) + f (0.4) + f (0.5)] (0.1)

  = [0.01 + 0.04 + 0.09 + 0.16 + 0.25](0.1) = 0.055. 

ஃ∫0.50 x2 dx- ன் தோராய மதிப்பு 0.055 ஆகும்.

(iii) சம அளவு ∆x கொண்ட ரீமன் கூட்டலுக்கான நடு-முனை விதியானது

S = [f (x0 + x1 / 2) + f (x1 + x2 / 2) + … + f (xn-1 + xn / 2)] ∆x

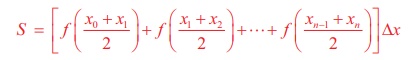
ஃS = [f (0.05) + f (0.15) + f (0.25) + f (0.35) + f (0.45) ] (0.1)

= [0.0025 + 0.0225 + 0.0625 + 0.1225 + 0.2025](0.1)

= 0.04125. 

ஃ∫0.50 x2 dx -ன் தோராய மதிப்பு 0.04125 ஆகும்.