காமா தொகையிடல் (Gamma Integral)

காமா தொகையிடல் (Gamma Integral)

இப்பகுதியில் ∞∫0 e −x xn−1dx , n ஓரு மிகை முழுக்கள் என்ற சிறப்பு வகை முறையற்ற தொகையிடலைப் பற்றி படிப்போம்.

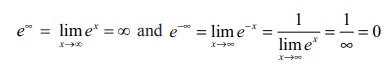
லோபிதாலின் விதிப்படி m என்ற முழுக்களின் ஒவ்வொரு எண்ணிற்கும் நாம் பெறுவது

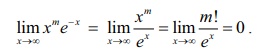
எடுத்துக்காட்டு 9.43

n ஓர் மிகை முழுக்கள் எனில் ∞∫0 e−x xn dx = n!, என நிறுவுக.

தீர்வு 

பகுதித் தொகையிடலைப் பயன்படுத்த நாம் பெறுவது

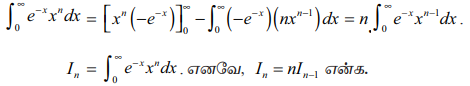
In = ∞∫0 e−x xn dx . எனவே, In = nIn−1 என்க.

மேலும் In = n ( n −1)In−2

இதே வழியை பின்பற்ற கடைசியாக நாம் பெறுவது

In = n ( n − 1)( n − 2) ---- ( 2)(1)I0 . 

ஆனால், I0 = ∞∫0 e −x x0dx = ( −e−x)∞0 = 0 +1 = 1. எனவே நாம் பெறுவது 

In = n (n − 1)(n − 2) … (2)(1) = n!. 

முடிவு

∞∫0 e −x xn dx = n!, n என்பது மிகை முழுக்கள்.

குறிப்பு

∞∫0 e−x xn−1dx  என்ற தொகையிடலானது ஒரே ஒரு மிகை முழு எண் n ≥ 1-க்கு வரையறுக்கப்பட்டு உள்ளது. 

வரையறை 9.1

∞∫0 e −x xn−1dx என்பது காமா தொகையிடல் (gamma integral) என அழைக்கப்படும். இதை T(n) என்ற குறியீட்டில் எழுதுவோம் மற்றும் “காமா n” எனப் படிப்போம்.

குறிப்பு

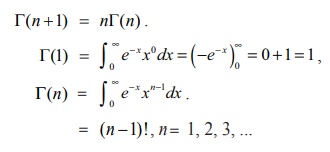
எடுத்துக்காட்டு 9.44

மதிப்பிடுக : ∞∫0 e −ax xn dx , a > 0.

 தீர்வு

t = ax என்க . dt = adx. x = 0 ⇒ t = 0 மற்றும் x = ∞ ⇒ t = ∞ 

எனவே, நாம் பெறுவது