12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 9 : தொகை நுண்கணிதத்தின் பயன்பாடுகள்
தொகை நுண்கணித அடிப்படைத் தேற்றங்கள் மற்றும் அவற்றின் பயன்பாடுகள் (Fundamental Theorems of Integral Calculus and their Applications)
தொகை நுண்கணித அடிப்படைத் தேற்றங்கள் மற்றும் அவற்றின் பயன்பாடுகள் (Fundamental Theorems of Integral Calculus and their Applications)
சார்பு மிக எளிமையாக இருப்பினும் b∫a f(x)dx -இன் மதிப்பை தொகையீடுகளின் கூட்டலின் எல்லைகளாக தீர்வு காண்பது மிகவும் கடினம் என்பதை மேலே உள்ள எடுத்துக்காட்டுகளில் நாம் கண்டோம் வாயிலாக பார்த்தோம். நியூட்டன் (Newton) மற்றும் லிபினிட்ஸ் (Leibnitz) இருவரும் கிட்டதட்ட ஒரே காலத்தில் வரையறுத்த தொகையிடலை ஓர் எளிய முறையில் காண வழிவகுத்தனர். இம்முறையானது முதல் மற்றும் இரண்டாம் நுண்கணித அடிப்படைத் தேற்றத்தை அடிப்படையாகக் கொண்டது. இத்தேற்றங்கள் ஒரு சார்பிற்கும் அதன் எதிர் வகையிடலுக்கும் (முடியும்மெனில்) உள்ள தொடர்பை நிலைநிறுத்துகிறது. இத்தேற்றங்கள் வகை நுண்கணிதத்திற்கும் தொகை நுண்கணிதத்திற்கும் உள்ள ஒரு தொடர்பை ஏற்படுத்துகிறது.
பின்வரும் முக்கிய தேற்றங்கள் நிரூபணயின்றி கீழே கொடுக்கப்பட்டுள்ளன
தேற்றம் 9.1 (முதல் தொகை நுண்கணித அடிப்படைத் தேற்றம்)
f (x) என்பது [a,b] என்ற மூடிய இடைவெளியில் வரையறுக்கப்பட்ட தொடர்ச்சியான சார்பு மற்றும் F(x) = x∫a f(u)du, a < x < b எனில், d/dx F(x) = f (x) . அதாவது F(x)-ஆனது f (x) -இன் எதிர் வகையீடு ஆகும்.
தேற்றம் 9.2 (இரண்டாவது தொகை நுண்கணித அடிப்படைத் தேற்றம்)
f (x) என்பது [a,b] என்ற மூடிய இடைவெளியில் வரையறுக்கப்பட்ட தொடர்ச்சியான சார்பு மற்றும் F(x)-ஆனது f (x) -இன் எதிர் வகையீடு எனில், b∫a f (x)dx = F(b) - F(a).
குறிப்பு
F(b) - F(a) ஆனது b∫af(x)dx என்ற வரையறுக்கப்பட்ட தொகையிடலின் (ரீமன் தொகையிடல்)மதிப்பானதால் எதிர்முறை வகையீடு F(x) உடன் சேர்க்கப்படும் தன்னிச்சை மாறி நீக்கப்பட்டு விடும். எனவே வரையறுத்த தொகையிடலின் மதிப்பு காணும்போது எதிர் வகையீடுடன் தன்னிச்சை மாறியை சேர்க்கத் தேவையில்லை . F(b) - F(a)-ஐ சுருக்கமாக [F(x)]ba என எழுதலாம். வரையறுத்த தொகையிடலின் மதிப்பு ஒருமைத் தன்மை உடையது.
இரண்டாவது தொகை நுண்கணித தேற்றத்தின் வாயிலாக பின்வரும் வரையறுத்த தொகையிடலின் பண்புகளைப் பெறுகிறோம். அவற்றை நிரூபணமின்றி இங்கு காண்போம்.
பண்பு 1 : b∫af (x)dx = b∫a f (u)du, a<b
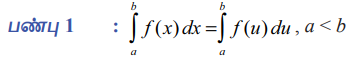
அதாவது எல்லைகள் மாறாமல் இருக்கும் போது மாறியை மாற்றுவதால் தொகையிடலின் மதிப்பு மாறாது.
பண்பு 2 : b∫a f (x)dx = - a∫b f (x)dx
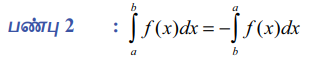
அதாவது வரையறுத்த தொகையிடலில் எல்லைகளை இடமாற்றம் செய்யும்போது வரையறுத்த தொகையிடலின் குறியீடு’ – ‘ஆக மாறும்.
பண்பு 3 :b∫a f (x)dx = c∫a f (x)dx + b∫c f (x)dx, a<c<b
பண்பு 4 :b∫a[af(x) + βg(x)|dx=a b∫a f(x)dx+ βb∫a g(x)dx இங்கு, a மற்றும்β பண்பு மாறிலிகள்.
பண்பு 5 : x = g(u) எனில், b∫a f(x)dx = d∫c f (g(u)) dg(u)/du du இங்கு g(c)=a மற்றும் g(d) = b
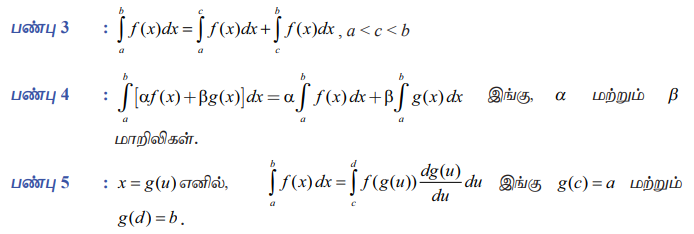
இப்பண்பானது வரையறுத்த தொகையிடலில் பிரதியிடல் முறையைப் பயன்படுத்த உதவுகிறது. மேற்கூறிய பண்புகளை பின்வரும் எடுத்துக்காட்டுகளில் பயன்படுத்துவோம்.


நிரூபணம்
u = a + b - x என்க . எனவே , dx = -du .
x = a எனில் u = a + b - a = b மற்றும் x = b எனில், u = a + b -b = a.
∴ b∫a f ( x)dx = a∫b f ( a + b −u)(−du) = b∫a f ( a + b −u)du
= ∫ab f ( a + b − x)dx .
குறிப்பு
a-க்கு பதில் 0 மற்றும் b -க்கு பதில் a என மேலே உள்ள பண்பில் பிரதியிட,
0 ∫ a f ( x) dx = ∫0a f ( a − x ) dx . என்ற பண்பு கிடைக்கும்.
எடுத்துக்காட்டு 9.19

பண்பு 8
f (x)ஓர் இரட்டைப்படைச் சார்பு எனில், a∫-a f ( x) dx = 2∫a0 f ( x) dx.
( f(x) ஓர் இரட்டைப்படைச் சார்பு எனில் f(-x) = f(x) எனஅறிவோம்)
நிரூபணம்
பண்பு 3-ன்படி
−a∫a f ( x) dx = −a∫0 f ( x) dx + 0∫a f ( x) dx . ----(1)
x = -u என ∫0-a f ( x) dx என்பதில் பிரதியிடுவோம் எனவே dx = -du.
x = -a எனில், u = a மற்றும் x = 0 எனில், u = 0. எனவே நாம் பெறுவது .
−a∫0 f ( x) dx = 0∫a f ( − u)( −du) = 0∫a f ( −u) du = 0∫a f ( − x) dx = 0∫a f ( x) dx . ... (2)
சமன்பாடு (2)-ஐ சமன்பாடு (1)-ல் பிரதியிடக் கிடைப்பது
−a∫a f ( x) dx = 0∫a f (x) dx + 0∫a f (x) dx = 20∫a f (x) dx .
பண்பு 9
f (x)ஓர் ஒற்றைப்படைச் சார்பு எனில், −a∫a f ( x) dx = 0.
( f(x) ஓர் ஒற்றைப்படைச் சார்பு எனில் f(-x)=- f(x) எனஅறிவோம்)
நிரூபணம்
பண்பு 3-ன் படி
∫a-a f ( x) dx = −a ∫ 0 f ( x) dx + 0∫a f ( x) dx . --- (1)
x = -u என −a∫0 f ( x) dx என்பதில் பிரதியிடுவோம் dx = -du.
x = -a எனில், u = a மற்றும் x = 0 எனில், u = 0. எனவே நாம் பெறுவது .
−a∫0 f ( x) dx = a ∫0 f ( − u)( −du) = a∫0 f ( −u) du = a ∫0 f ( − x) dx = − a ∫0 f( x) dx . ... (2)
சமன்பாடு (2)-ஐ சமன்பாடு (1)-ல் பிரதியிடக் கிடைப்பது
a∫−a f ( x) dx = a∫0 f ( x) dx − a∫0 f ( x) dx = 0
பண்பு 10
f(2a-x)=f(x) எனில் 2a∫0 f ( x) dx = 2 a∫0 f ( x) dx.
நிரூபணம்
பண்பு 7-ன் படி
2a∫0 f ( x) dx = a∫0 [ f ( x) + f ( 2a − x ) ] dx. ...(1)
f(2a-x)=f(x) என சமன்பாடு (1)-ல் பிரதியிடக் கிடைப்பது
0∫2a f (x) dx = a∫0 [ f (x ) + f (x)]dx = 2 a∫0 f (x) dx.
பண்பு 11
f(2a -x) = -f(x) எனில், ∫2a0 f( x) dx = 0. ஆகும்.
நிரூபணம்
பண்பு 7-ன் படி,
2a ∫0 f ( x) dx = a∫0 [ f ( x) + f ( 2a − x ) ]dx. ... (1)
f(2a-x) = -f (x) என சமன்பாடு (1)-ல் பிரதியிட நமக்குக் கிடைப்பது,
∫2a0 f ( x) dx = ∫a0 [ f ( x ) − f ( x)]dx = 0.
பண்பு 12
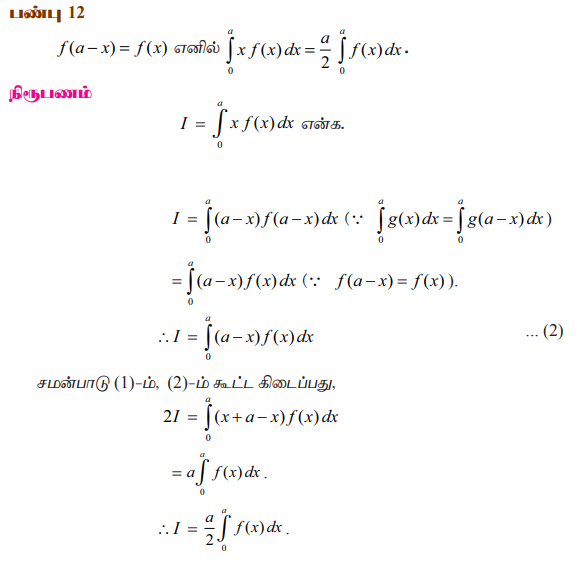
குறிப்பு
இடது புறத்தில் உள்ள தொகைச்சார்பில் உள்ள x என்ற காரணியை நீக்க இப்பண்பு உதவுகிறது
எடுத்துக்காட்டு 9.20
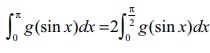 என நிறுவுக. இங்கு g(sin x) என்பது sin x -ஐ கொண்டசார்பு.
என நிறுவுக. இங்கு g(sin x) என்பது sin x -ஐ கொண்டசார்பு.
தீர்வு
f(2a-x) = f (x) எனில் 2a∫0 f ( x) dx = 2 a∫0 f ( x) dx
2a = π மற்றும் f (x) = g(sin x) என எடுத்துக் கொள்க.
எனவே , f (2a-x) = g(sin(π- x)) = g(sin x) = f (x)
∴∫2a0 f (x) dx = 2∫a0 f (x) dx .
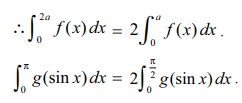
முடிவு
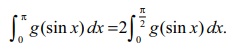
குறிப்பு
π∫0 g (sin x) dx என்ற அமைப்பில் உள்ள வரையறுத்த தொகையிடல்களை காண மேலே உள்ளமுடிவு பயன்படும்.
எடுத்துக்காட்டு 9.21

எடுத்துக்காட்டு 9.22
2π∫0 g (cos x) dx =20∫π g (cos x) dx எனக் காட்டுக. இங்கு g(cos x) என்பது cos x-ல் அமைந்தசார்பு.
தீர்வு
2a = 2π மற்றும் f (x) = g(cos x) என்க .
எனவே, f(2a-x) = f (2π - x) = g(cos(2π - x)) = g(cos x) = f (x)
∴ ∫2a0 f (x) dx = 2 a∫0 f (x) dx .
∴ ∫2a0 g (cos x) dx = 2 π∫0 g (cos x) dx .
முடிவு
2π∫0 g (cos x) dx =2 π∫0 g (cos x) dx.
குறிப்பு
2π∫0 g (cos x) dx. என்ற அமைப்பில் உள்ள வரையறுத்த தொகையிடல்களை காண மேலே உள்ள முடிவு பயன்படும்.
எடுத்துக்காட்டு 9.23
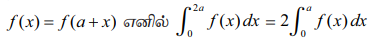
தீர்வு
x = a +u எனப் பிரதியிடக் கிடைப்பது dx = du ; x = a எனில் u = 0 , x = 2a எனில்,
u = a.
∴2a∫a f (x) dx = a∫0 f (a + u ) du = a∫0 f (u ) du , since f (x) = f (a + x)
= a∫0 f (x) dx . ... (2)
சமன்பாடு (2)-ஐ (1)-ல் பயன்படுத்தக் கிடைப்பது,
2a∫0 f (x) dx = 2a∫0 f (x) dx .
எடுத்துக்காட்டு 9.24
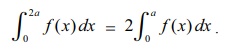
தீர்வு
f (x) = x cos x என்க .f (-x) = (-x) cos(-x) = -xcos x = -f (x)
எனவே, f (x) = xcos x ஓர் ஒற்றைப் படைச் சார்பாகும். f (x) என்ற ஒற்றைப் படை சார்பிற்கு

எடுத்துக்காட்டு 9.25
