பெரு வினாக்கள், இயற்பியல் - நிலை மின்னியல்: பெரு வினாக்கள் | 12th Physics : UNIT 1 : Electrostatics
12 வது இயற்பியல் : அலகு 1 : நிலை மின்னியல்
நிலை மின்னியல்: பெரு வினாக்கள்
III. பெரு வினாக்கள்
1. மின்துகள்களின் அடிப்படைப் பண்புகள் குறித்து விவாதிக்க.
• மின்னூட்டம் என்பது உள்ளார்ந்த அடிப்படை பண்பாகும்.
மின்னூட்ட மாறாத் தன்மை:
• பிரபஞ்சத்திலுள்ள மொத்த மின்னூட்டம் மாறாமல் இருக்கும்.
• மின்னூட்டத்தை ஆக்கவோ அழிக்கவோ இயலாது.
• எந்தவொரு இயற்கை நிகழ்விலும் மொத்த மின்னூட்ட மாற்றம் சுழியாகவே இருக்கும்.
மின்னூட்டத்தின் குவாண்டமாக்கல்:
• எந்தவொரு பொருளில் உள்ள மின்னூட்டத்தின் மதிப்பு அடிப்படை மதிப்பின் முழு மடங்காகவே இருக்கும்.
q = ne
n என்பது ஒரு முழுஎண்
e என்பது அடிப்படை மின்னூட்டம்
e = 1.6×10 −19 C
2. கூலூம் விதி மற்றும் அதன் பல்வேறு தன்மைகள் குறித்து விரிவாகக் கூறுக.
கூலூம் விதி:
வெற்றிடத்தில் r தொலைவில் பிரித்து வைக்கப்பட்டுள்ள இரு நிலையாகவுள்ள புள்ளி மின்துகள்களை அவற்றின் மின்னூட்டங்கள் முறையே q1 மற்றும் q2 ஆகும். கூலூம் விதிப்படி புள்ளி மின்துகள் q2 வின் மீது புள்ளி மின்துகள் q1 செயல்படுத்தும் விசையானது பின்வருமாறு எழுதப்படுகிறது.
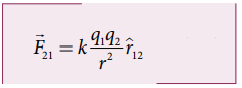
கூலூம் விதியின் முக்கிய இயல்புகள்:
• நிலைமின் விசையானது புள்ளி மின்துகள்களின் மின்னூட்ட மதிப்பின் பெருக்கற்பலனுக்கு நேர்த்தகவிலும் அவற்றிற்கு இடையே உள்ள தொலைவின் இருமடிக்கு எதிர்த்தகவிலும் இருக்கும்.
• q2 மின்துகளின் மீது q1 மின்துகள் செலுத்தும் விசை அவற்றை இணைக்கும் கோட்டின் திசையிலேயே இருக்கும். இதில் r12 என்ற ஓரலகு வெக்டரானது மின்துகள் q1 லிருந்து q2 வை நோக்கிய திசையிலிருக்கும். அதேபோல், q1 இன் மீது q2 செலுத்தும் விசை −r12 திசையிலிருக்கும் (அதாவது ![]() ன் திசைக்கு எதிர்த்திசையில்)
ன் திசைக்கு எதிர்த்திசையில்)
• SI அலகு முறையில், K = 1/4πεo மற்றும் K ன் மதிப்பு 9 × 109 Nm2C−2 என்றும் கண்டறியப்பட்டுள்ளது.
இங்கு εo என்பது வெற்றிடத்தின் விடுதிறன் (Permittivity of free space) எனப்படும். அதன் மதிப்பு
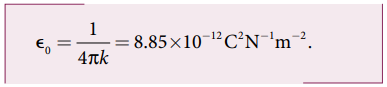
• ஒரு கூலூம் மின்னூட்ட மதிப்பு கொண்ட ஒரு மீட்டர் இடைவெளியில் வைக்கப்பட்டுள்ள இரு மின்துகள்களுக்கு இடையே செயல்படும் விசையின் மதிப்பைப் பின்வருமாறு கணக்கிடலாம்.
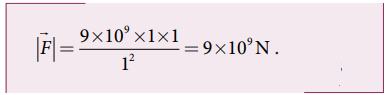
• வெற்றிடத்தில் உள்ள புள்ளி மின்துகள்களுக்கு இடையிலான விசையை விட பிற ஊடகங்களில் செயல்படும் விசை குறைவாக இருக்கும்.
• εr = ε / εo வெற்றிடம் மற்றும் காற்றில் εr = 1 மற்ற ஊடகங்களுக்கு εr > 1
3. மின்புலத்தை வரையறுத்து அதன் பல்வேறு தன்மைகளை விவாதிக்க.
• ஓரலகு மின்னூட்டம் கொண்ட மின்துகளால் உணரப்படும் விசையே அப்புள்ளியில் உள்ள மின்புலத்தின் மதிப்பாகும்.
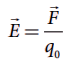
மின்புலத்தின் முக்கிய பண்புகள்:
• மின்துகள் q நேர் மின்னூட்டம் (+) கொண்டதாக இருந்தால், மின்துகளிலிருந்து வெளிநோக்கிய திசையில் மின்புலம் இருக்கும். q எதிர்மின்னூட்டம் (−) கொண்டதாக இருந்தால் உள்நோக்கிய திசையில் மின்புலம் இருக்கும்.
• P என்ற ஒரு புள்ளியில் மின்புலம் ![]() , எனில், அப்புள்ளியில் வைக்கப்படும் சோதனை மின்துகள் qo ஆல் உணரப்படும் விசை.
, எனில், அப்புள்ளியில் வைக்கப்படும் சோதனை மின்துகள் qo ஆல் உணரப்படும் விசை.
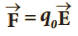
• மின்புலமானது சோதனை மின்துகளின் மின்னூட்டம் qo ஐச் சார்ந்ததல்ல என்பதையும் மூல மின்துகளின் (Source charge) மின்னூட்ட மதிப்பு, q ஐ மட்டுமே சார்ந்தது.
4. மின் இருமுனை ஒன்றினால் அதன் அச்சுக்கோடு மற்றும் நடுவரைக் கோட்டில் ஏற்படும் மின்புலத்தைக் கணக்கிடுக.
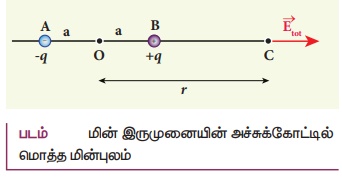
நேர்வு (i) இருமுனையில் அச்சுக்கோட்டில் மின் இருமுனையால் உருவாகும் மின்புலம்
• X − அச்சில் வைக்கப்பட்டுள்ள மின் இருமுனை ஒன்றைக் கருதுவோம்.
• அதன் மையப்புள்ளி O விலிருந்து அச்சுக் கோட்டில் r தொலைவில் புள்ளி C உள்ளது.
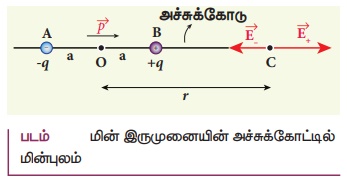
• +q மின்னூட்ட மதிப்பு கொண்ட மின்துகள்களால் புள்ளி Cல் உருவாகும் மின்புலம்
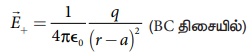
• மின் இருமுனை திருப்புத்திறன் வெக்டர் ![]() ஆனது −q விலிருந்து +q வை நோக்கிய திசையில், அதாவது BC திசையில் இருப்பதால்,
ஆனது −q விலிருந்து +q வை நோக்கிய திசையில், அதாவது BC திசையில் இருப்பதால்,
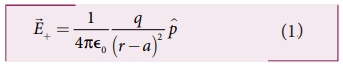
• இங்கு ![]() ஆனது −q விலிருந்து +q வை நோக்கிய திசையில் வரையப்படும் இருமுனை திருப்புத்திறனின் ஓரலகு வெக்டராகும்.
ஆனது −q விலிருந்து +q வை நோக்கிய திசையில் வரையப்படும் இருமுனை திருப்புத்திறனின் ஓரலகு வெக்டராகும்.
• −q மின்னூட்ட மதிப்பு கொண்ட மின்துகளால் புள்ளி Cல் உருவாகும் மின்புலம்
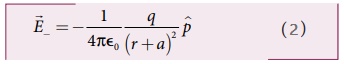
• −q மின்துகளை விட +q மின்துகளானது புள்ளி Cக்கு அருகில் உள்ளதால் ![]() ஐ விட
ஐ விட ![]() வலிமையானது.
வலிமையானது.
• புள்ளி Cல் உருவாகும் மொத்த மின்புலத்தைக் கணக்கிட மின்புலங்களின் மேற்பொருந்துதல் தத்துவம் பயன்படுத்தப்படுகிறது.

• −q வைக் காட்டிலும் +q மின்துகள்கள் புள்ளி Cக்கு அருகில் இருப்பதால் மொத்த மின்புலத்தின் திசையும் ![]() + . திசையிலேயே அமைந்துள்ளது.
+ . திசையிலேயே அமைந்துள்ளது.
• மின் இருமுனையிலிருந்து புள்ளி C வெகு தொலைவில் இருந்தால் (r >> a) மேலும் (r2 – a2)2 ≈ r4 எனலாம். இதை சமன்பாடு (4)ல் பிரதியிட
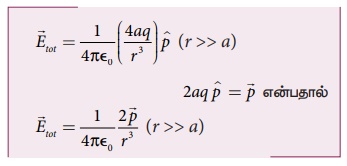
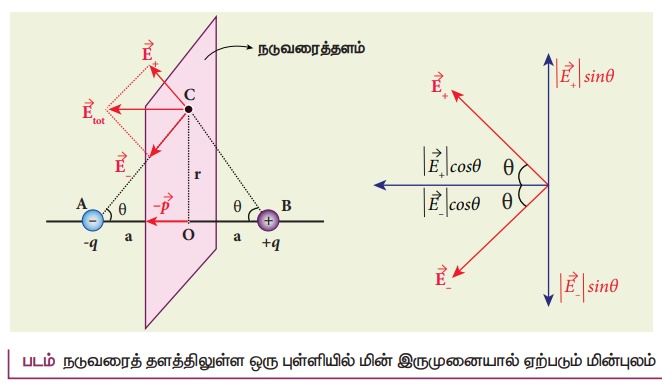
நேர்வு (ii) மின் இருமுனையின் நடுவரைத் தளத்திலுள்ள புள்ளியில் மின்புலம்:
• மின் இருமுனையின் நடுப்புள்ளி O விலிருந்து r தொலைவில் நடுவரைத் தளத்தில் அமைந்த புள்ளி C ஐக் கருதுவோம்.
• +q மற்றும் −q இரண்டிலிருந்தும் புள்ளி C சம தொலைவில் உள்ளதால் அவற்றினால் உருவாகும் மின்புலங்களின் எண்மதிப்பு சமமாகும்.
• ![]() + இன் திசை BC இன் திசையிலும்
+ இன் திசை BC இன் திசையிலும் ![]() _ இன் திசை CA வழியாகவும் செயல்படும்.
_ இன் திசை CA வழியாகவும் செயல்படும்.
• ![]() + மற்றும்
+ மற்றும் ![]() _ இவற்றை இரு கூறுகளாகப் பகுப்போம்.
_ இவற்றை இரு கூறுகளாகப் பகுப்போம்.
• புள்ளி Cல் ஏற்படும் மொத்த மின்புலத்தின் எண்மதிப்பானது E+ மற்றும் E_ ஆகியவற்றின் இணைக் கூறுகளின் கூடுதலுக்குச் சமமாகவும் Pன் திசையிலும் இருக்கும்.
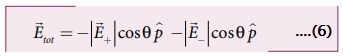
• மின்புலம் ஒரு வெக்டர் அளவு என்பதால் அதற்கு தனித்தவொரு திசையும் எண்மதிப்பும் வெளியிலுள்ள ஒவ்வொரு புள்ளியிலும் இருக்கும்.
• சோதனை மின்துகள் (qo) வைக்கப்படும் போது மூல மின்துகள் நகராமல் இருப்பதற்காக அதன் மின்னூட்ட மதிப்பு qo மிகவும் சிறியதாக எடுத்துக் கொள்ளப்படுகிறது.
• மின்துகள்களின் தொடர் பரவல்களுக்கும், வரம்பிற்குட்பட்ட மின்னூட்ட அளவு கொண்ட மின்துகள் பரவல்களுக்கும் தொகையிடல் முறைகளைப் பயன்படுத்த வேண்டும்.
• மின்புலங்களில் இரு வகைகள் உள்ளன : சீரான (மாறாத) மின்புலம் மற்றும் சீரற்ற மின்புலம். புறவெளியில் (space) உள்ள அனைத்து புள்ளிகளிலும் ஒரே திசையுடன் மாறாத எண்மதிப்பும் கொண்டிருந்தால் அது சீரான மின்புலம் (uniform electric field) எனப்படும். புறவெறியில் வெவ்வேறு புள்ளிகளில் வெவ்வேறு திசைகள் அல்லது வெவ்வேறு எண்மதிப்புகள் அல்லது இவ்விரண்டுமே கொண்டிருந்தால் அது சீரற்ற மின்புலமாகும்.
5. சீரான மின்புலத்தில் வைக்கப்படும் மின் இருமுனை மீது செயல்படும் திருப்பு விசையின் கோவையைப் பெறுக.
• சம இடைவெளியில் ஒரே திசையிலமைந்த மின்புலக் கோடுகளினால் குறிக்கப்படும் சீரான மின்புலம் ![]() ஒன்றில் வைக்கப்பட்டுள்ள இருமுனை திருப்புத்திறன்
ஒன்றில் வைக்கப்பட்டுள்ள இருமுனை திருப்புத்திறன் ![]() கொண்ட மின் இருமுனை ஒன்றைக் கருதுவோம்.
கொண்ட மின் இருமுனை ஒன்றைக் கருதுவோம்.
• +q மின்துகளானது மின்புலத்தின் திசையில் q ![]() என்ற விசையையும் − q மின்துகளானது புலத்திற்கு எதிர்த்திசையில் − q
என்ற விசையையும் − q மின்துகளானது புலத்திற்கு எதிர்த்திசையில் − q ![]() என்ற விசையையும் உணர்கின்றன.
என்ற விசையையும் உணர்கின்றன.
• புற மின்புலம் மொத்த விசை சுழியாகும்.
• இவ்விரண்டு விசைகளும் வெவ்வேறு புள்ளிகளில் செயல்படுவதால் இரட்டை உருவாகிறது.
• அதனால் ஏற்படும் திருப்பு விசை மின் இருமுனையின் மீது செயல்பட்டு அதை சுழலச் செய்கிறது.
• புள்ளி O வைப் பொருத்து மின் இருமுனையின் மீது செயல்படும் திருப்புவிசை
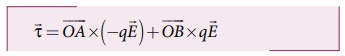
• மொத்த திருப்புவிசையின் எண்மதிப்பு
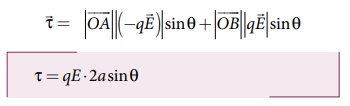
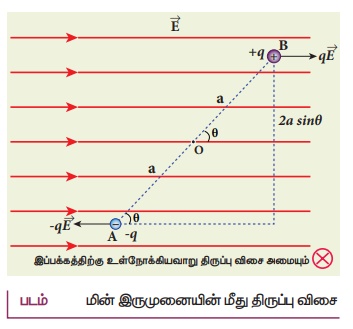
இப்பக்கத்திற்கு உள்நோக்கியவாறு திருப்புவிசை அமையும்.
மின் இருமுனையின் மீது திருப்பு விசை
• இங்கு θ என்பது ![]() மற்றும்
மற்றும் ![]() க்கு இடைப்பட்ட கோணம். மேலும் p = 2aq.
க்கு இடைப்பட்ட கோணம். மேலும் p = 2aq.

• இத்திருப்புவிசையின் எண்மதிப்பு τ=pE; θ = 90o ஆகும் போது, அது பெரும மதிப்பை அடையும்.
• இந்தத் திருப்பு விசையானது மின் இருமுனையைச் சுழலச் செய்து மின்புலத்தின் (![]() ) திசையில் அதை ஒருங்கமையச் செய்கிறது. மின்புலத்துடன் (
) திசையில் அதை ஒருங்கமையச் செய்கிறது. மின்புலத்துடன் (![]() ) திருப்புத்திறன் (
) திருப்புத்திறன் (![]() ) ஒருங்கமைந்த பின், இருமுனையின் மீது செயல்படும் மொத்த திருப்புவிசை சுழியாகும்.
) ஒருங்கமைந்த பின், இருமுனையின் மீது செயல்படும் மொத்த திருப்புவிசை சுழியாகும்.
• மின்புலம் சீரற்றதாக இருந்தால் +q ன் மீதான விசையும் –q ன் மீதான விசையும் வெவ்வேறாக இருக்கும். இந்நிலையில் திருப்பு விசையுடன் நிகர விசை ஒன்றும் இருமுனையின் மீது செயல்படும்.
6. புள்ளி மின்துகள் ஒன்றினால் ஏற்படும் நிலை மின்னழுத்தத்திற்கான கோவையைத் தருவிக்க.
• ஆதிப்புள்ளியில் நிலையாக வைக்கப்பட்டுள்ள q மின்னூட்ட மதிப்பு கொண்ட நேர் மின்துகள் ஒன்றைக் கருதவும். புள்ளி P அதிலிருந்து r தொலைவில் உள்ளது.
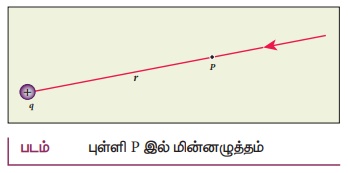
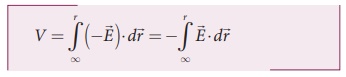
• புள்ளி நேர் மின்துகள் q வினால் உருவாகும் மின்புலம்
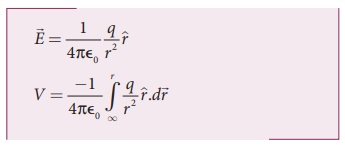
• மீச்சிறு இடப்பெயர்ச்சி வெக்டர் 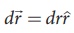 மற்றும்
மற்றும் 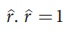 எனவே
எனவே
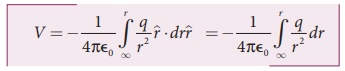
தொகயிடலுக்குப் பின்
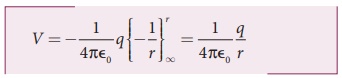
ஆகவே, புள்ளி மின்துகளினால் r தொலைவில் ஏற்படும் மின்னழுத்தம்

7. மின் இருமுனை ஒன்றினால் ஏற்படும் நிலை மின்னழுத்தத்திற்கான கோவையைப் பெறுக.
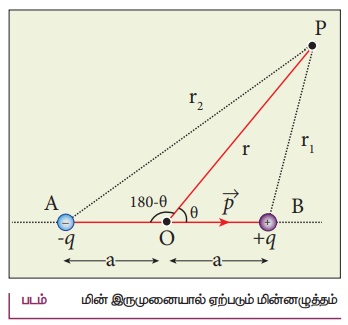
மின் இருமுனையால் ஏற்படும் மின்னழுத்தம்
• 2a என்ற சிறிய இடைவெளியில் பிரிக்கப்பட்டுள்ள இரு சமமான, வேறின மின்துகள்களைக் கருதுவோம்.
• மின் இருமுனையின் நடுப்புள்ளியிலிருந்து r தொலைவில் P என்ற புள்ளி உள்ளது. AB என்ற இருமுனை அச்சுக்கும் OP என்ற கோட்டிற்கும் இடையேயுள்ள கோணம் θ என்க.
• +q விலிருந்து புள்ளி P ன் தொலைவு r1 எனவும் −q விலிருந்து புள்ளி Pன் தொலைவு r2 எனவும் கொள்க.
• +q மின்துகளினால் புள்ளி p ல் உருவாகும் மின்னழுத்தம் = 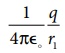
• −q மின்துகளினால் புள்ளி P ல் உருவாகும் மின்னழுத்தம் = 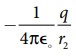
• புள்ளி P ல் உருவாகும் மொத்த மின்னழுத்தம்,
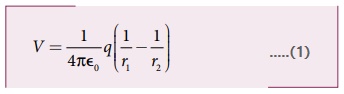
• BOP, முக்கோணத்தில் கொசைன் விதியைப் பயன்படுத்த
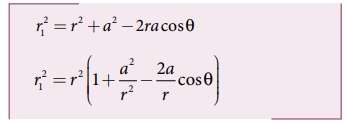
a < < r. இதனால் a2/r2 − இன் மதிப்பு மிகவும் சிறியது. எனவே அதைப் புறக்கணிக்கலாம்.
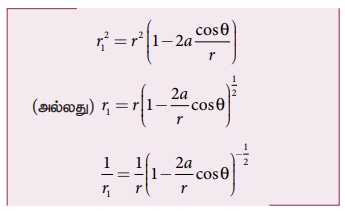
• a/r <<1, ஆதலால் ஈருறுப்புத் தேற்றத்தைப் பயன்படுத்தி உயர் அடுக்குகளைப் புறக்கணித்து எழுதினால்,

• இதேபோல் AOP முக்கோணத்திற்கு கொசைன் விதியைப் பயன்படுத்த.
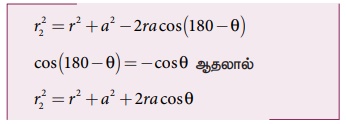
a2/r2 ஐப் புறக்கணிக்க
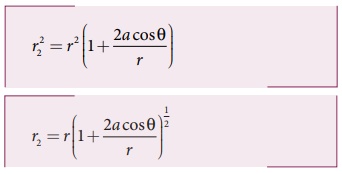
ஈருறுப்புத் தேற்றத்தைப் பயன்படுத்தினால்,
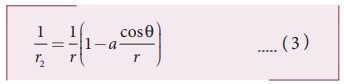
• சமன்பாடு (2) மற்றும் (3) ஆகியவற்றை சமன்பாடு (1) ல் பிரதியிட
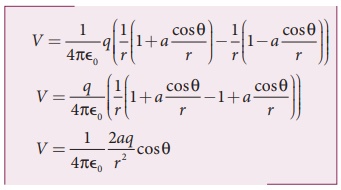
• மின் இருமுனையின் திருப்புத்திறன் p= 2qa எனவே,
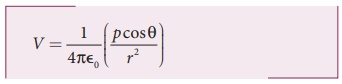
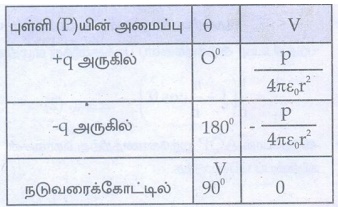
• p cosθ = ![]() என எழுதலாம். இங்கு
என எழுதலாம். இங்கு ![]() என்பது புள்ளி O விலிருந்து புள்ளி P ஐ நோக்கி உள்ள ஓரலகு வெக்டராகும். எனவே மின் இருமுனையால் ஒரு புள்ளியில் உருவாகும் மின்னழுத்தம்
என்பது புள்ளி O விலிருந்து புள்ளி P ஐ நோக்கி உள்ள ஓரலகு வெக்டராகும். எனவே மின் இருமுனையால் ஒரு புள்ளியில் உருவாகும் மின்னழுத்தம்
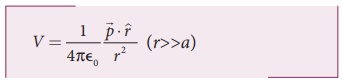
8. வரம்பிற்குட்பட்ட தொலைவுகளில் பிரித்து வைக்கப்பட்டுள்ள மூன்று புள்ளி மின்துகள்களின் தொகுப்பினால் ஏற்படும் நிலை மின்னழுத்த ஆற்றலுக்கான கோவையைப் பெறுக.
• மூன்று மின்துகள்கள் பின்வருமாறுள்ள நிலையமைப்பில் வைக்கப்பட்டுள்ளன.
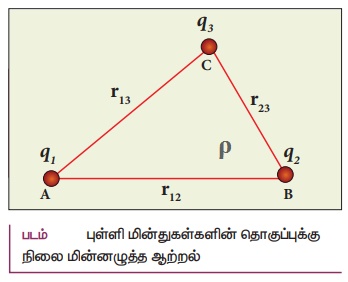
• q1 மின்துகளுக்கு அருகில் வேறு எந்த மின்துகள்களும் தொடக்கத்தில் இல்லாததால் முடிவிலாத் தொலைவிலிருந்து அதை புள்ளி A வரை கொண்டு வர எந்த வேலையும் செய்யத் தேவையில்லை.
• q2 மதிப்புடைய இரண்டாவது மின்துகளை புள்ளி Bக்கு கொண்டு வர q1 உருவாக்கிய மின்புலத்திற்கு எதிராக வேலை செய்யப்பட வேண்டும். q2 ன் மீது செய்யப்படும் வேலை W = q2 V1B இங்கு V1B என்பது முதல் மின்துகள் q1 ஆல் புள்ளி Bல் ஏற்படும் நிலை மின்னழுத்தம்

• இதேபோல், மூன்றாவது மின்துகள்கள் q3ஐ புள்ளி Cக்கு கொண்டு வர q2 மற்றும் q3 மின்துகள்கள் சேர்ந்து உருவாக்கும் மொத்த மின்புலத்திற்கு எதிராக வேலை செய்யப்பட வேண்டும். நிலை மின்னழுத்த ஆற்றல்
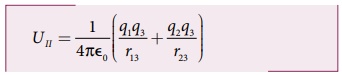
• மின்துகள் அமைப்பினால் உருவாக்கப்படும் மொத்த நிலை மின்னழுத்த ஆற்றல்,
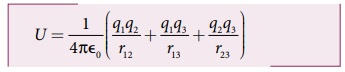
• சேமிக்கப்படும் நிலை மின்னழுத்த ஆற்றல் U ஆனது அம்மூன்று மின்துகள்களையும் குறிப்பிடப்பட்ட புள்ளிகளில் நிலைநிறுத்தச் செய்யப்படும் வேலைக்குச் சமமாகும்.
9. சீரான மின்புலத்தில் வைக்கப்படும் மின் இருமுனையின் நிலை மின்னழுத்த ஆற்றலுக்கான சமன்பாட்டை வருவிக்க.
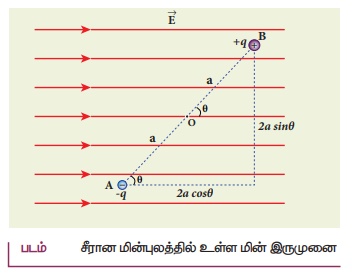
சீரான மின்புலத்தில் உள்ள இருமுனை
• சீரான மின்புலம் ![]() ஒன்றில் வைக்கப் பட்டுள்ள மின் இருமுனையைக் கருதுவோம்.
ஒன்றில் வைக்கப் பட்டுள்ள மின் இருமுனையைக் கருதுவோம்.
• சீரான மின்புலத்தில் வைக்கப்படும் இரு முனையின் மீது ஒரு திருப்புவிசை செயல்படும். இத்திருப்பு விசையானது மின்புலத்தின் திசையில் இருமுனையை ஒருங்கமைக்கின்றது.
• மின்புலத்தால் செலுத்தப்படும் இத்திருப்பு விசைக்கு எதிராக தொடக்கக்கோணம் θ’ இலிருந்து இறுதிகோணம் θ வரை இருமுனையை சுழலச் செய்ய, மின்புலத்தால் கொடுக்கப்படும் திருப்புவிசைக்கு சமமானதும், எதிர்த்திசையில் உள்ளதுமான புறத்திருப்புவிசை ஒன்றை இருமுனையின் மீது செயல்படுத்த வேண்டும்.

• 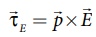 க்கு சமமாகவும் எதிர்த்திசையிலும்
க்கு சமமாகவும் எதிர்த்திசையிலும் ![]() உள்ளதால்,
உள்ளதால்,
• 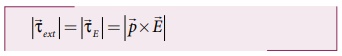

• இந்த வேலையானது கோண நிலைகள் θ மற்றும் θ' க்கு இடையேயுள்ள மின்னழுத்த ஆற்றல் வேறுபாட்டுக்குச் சமமாகும்.
• U(θ) – U(θ') = ΔU = −pEcosθ + pEcosθ' தொடக்கக் கோணம் θ' = 90o என்றும் இதையே சுட்டுப்புள்ளியாகவும் (reference point) எடுத்துக்கொண்டால் U(θ') = pE cos 90o = 0.
• எனவே சீரான மின்புலத்தில் வைக்கப்பட்டுள்ள இருமுனை அமைப்பு ஒன்றில் சேமிக்கப்படும் மின்னழுத்த ஆற்றல்
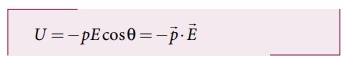
• p மற்றும் Eஐத் தவிர மின்னழுத்த ஆற்றலானது புற மின்புலத்தைப் பொறுத்து மின் இருமுனையின் திசையமைப்பையும் சார்ந்திருக்கும்.
• புறமின்புலத்துக்கு எதிரிணையாக (θ = π) இருமுனைத் திருப்புத்திறன் அமையும்போது மின்னழுத்த ஆற்றல் பெருமமாகவும் புறமின்புலத்துக்கு இணையாக (θ = 0o) இருமுனைத் திருப்புத்திறன் அமையும் போது மின்னழுத்த ஆற்றல் சிறுமமாகவும் இருக்கும்.
10. கூலூம் விதியிலிருந்து காஸ் விதியைப் பெறுக.
• Q மின்னூட்ட மதிப்புடையவொரு புள்ளி மின் துகள்களைச் சுற்றி r ஆரம் கொண்ட கற்பனைக் கோளம் ஒன்றைக் கருதவேண்டும்.
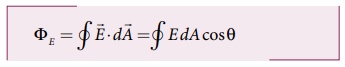
• இப்புள்ளி நேர் மின்துகளின் மின்புலமானது கோளப் பரப்பின் ஒவ்வொரு புள்ளியிலும் ஆர வழியே வெளிநோக்கிய திசையில் அமைகின்றது. எனவே, பரப்புக்கூறு ![]() ஆனது மின்புலத்தின் திசையிலேயே உள்ளதால் θ = 0o.
ஆனது மின்புலத்தின் திசையிலேயே உள்ளதால் θ = 0o.
• 
• கோளத்தின் பரப்பில் E சீராக உள்ளதால்
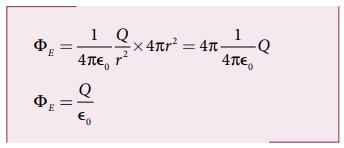
இந்த சமன்பாடு காஸ்விதி எனப்படும்.
11. மின்னூட்டம் பெற்ற முடிவிலா நீளமுள்ள கம்பியினால் ஏற்படும் மின்புலத்திற்கான சமன்பாட்டைப் பெறுக.
• λ எனும் சீரான மின்னூட்ட நீள் அடர்த்தி கொண்ட முடிவிலா நீளமுடைய கம்பியைக் கருதுவோம்.
• கம்பியிலிருந்து r செங்குத்துத் தொலைவில் புள்ளி P உள்ளது. காஸ் விதியைப் பயன்படுத்தி P இல் உருவாகும் மின்புலத்தைக் கணக்கிடலாம்.
• புள்ளி P இலிருந்து சம தொலைவில், கம்பியில் அமைந்துள்ள இரு சிறிய மின்துகள் கூறுகளை எடுத்துக் கொள்வோம்.
• இவ்விரு மின்துகள் கூறுகளினால் உருவாகும் தொகுபயன் மின்புலமானது மின்னூட்டம் பெற்ற கம்பியிலிருந்து ஆர வழியே வெளிநோக்கிய திசையில் அமைகின்றது. மேலும், r ஆரமுடைய வட்டத்தின் அனைத்துப் புள்ளிகளிலும் அதன் எண்மதிப்பு சமமாக இருக்கும்.
• இந்தப் பண்பின் அடிப்படையில் மின்னூட்டம் பெற்ற கம்பி உருளை வடிவ சமச்சீர் தன்மை உடையது எனலாம். எனவே r ஆரமும் L நீளமும் கொண்ட உருளை வடிவ காஸியன் பரப்பைக் கருதுவோம்.
• இப்பரப்பிற்கான மொத்த மின்பாயத்தை பின்வருமாறு கணக்கிடலாம்.
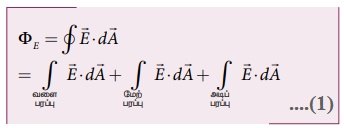
வளைபரப்பில் ![]() ஆனது
ஆனது ![]() க்கு இணையாக உள்ளதால்
க்கு இணையாக உள்ளதால் ![]() = EdA. மேல் மற்றும் அடிப்பரப்புக்கு
= EdA. மேல் மற்றும் அடிப்பரப்புக்கு ![]() ஆனது
ஆனது ![]() செங்குத்தாக உள்ளதால்
செங்குத்தாக உள்ளதால் ![]() = 0.
= 0.
• காஸ் விதியை உருளை வடிவ பரப்பிற்கு பயன்படுத்தினால்
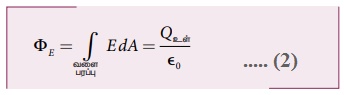
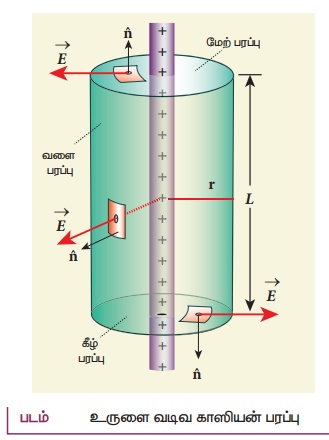
மின்னூட்டம் பெற்ற முடிவிலா நீளம் உடைய கம்பியினால் ஏற்படும் மின்புலம்
• மொத்த வளை பரப்பைப் பொருத்தவரை மின்புலத்தின் எண் மதிப்பு மாறிலியாக உள்ளதால், E ஆனது தொகையிடல் குறியீட்டுக்கு வெளியே எடுக்கப்படுகிறது. மேலும்

• இங்கு

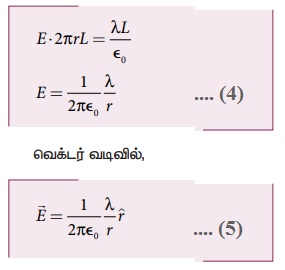
• புள்ளி மின்துகள் ஒன்றின் மின்புலம் 1/r என்றவாறு இருப்பதை அறிவோம். மாறாக மின்னூட்டம் பெற்ற முடிவிலா நீளமுடைய கம்பியின் மின்புலம் 1/r2 என்றவாறு அமைந்துள்ளது. கம்பிக்கு செங்குத்தான திசையிலேயே ![]() மின்புலம் அமைந்துள்ளது.
மின்புலம் அமைந்துள்ளது.
12. மின்னூட்டம் பெற்ற முடிவிலா சமதளப் பரப்பினால் ஏற்படும் மின்புலத்திற்கான சமன்பாட்டை வருவிக்க.
• σ எனும் சீரான மின்னூட்டப் பரப்படர்த்தி கொண்ட முடிவிலா சமதளத்தட்டு ஒன்றைக் கருதுவோம்.
• அத்தட்டிலிருந்து r தொலைவில் P என்ற புள்ளி உள்ளது.
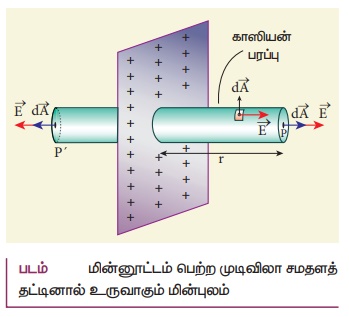
உருளை வடிவ முடிவிலா சமதளத் தட்டினால் உருவாகும் மின்புலம்
• சமதளத்தின் அளவு முடிவிலாதது என்பதால், அதிலிருந்து சம தொலைவில் உள்ள அனைத்து புள்ளிகளிலும் மின்புலத்தின் மதிப்பு சமமாக இருக்கும்.
• அனைத்து புள்ளிகளிலும் மின்புலத்தின் திசை ஆர வழியே அமைந்திருக்கும். 2r நீளமும் A குறுக்குவெட்டுப் பரப்பு கொண்ட உருளை வடிவ காஸியன் பரப்பைக் கருதுவோம்.
• அதன் நடுப்பகுதி வழியாக முடிவிலா சமதளத்தட்டு கடப்பதாகக் கொள்வோம். இவ்வுருளை வடிவ பரப்புக்கு காஸ் விதியைப் பயன்படுத்தினால்,
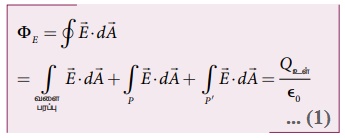
• வளைபரப்பின் மேலுள்ள அனைத்து புள்ளிகளிலும் மின்புலமானது பரப்பளவுக் கூறுகளுக்கு செங்குத்தாகவும், P மற்றும் P' பரப்புகளில் அது இணையாகவும் இருக்கிறது.
எனவே,
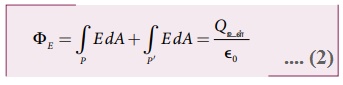
• இவ்விரு பரப்புகளுக்கும் மின்புலத்தின் எண் மதிப்பு சீராக உள்ளதால் தொகையிடல் குறியீட்டுக்கு வெளியே
Qஉள் = σ A எனவே,

P அல்லது P' பரப்பின் மொத்த பரப்பளவு

இங்கு ![]() என்பது சமதளத்திற்கு செங்குத்தாக, வெளிநோக்கிய திசையிலுள்ள ஓரலகு வெக்டராகும்.
என்பது சமதளத்திற்கு செங்குத்தாக, வெளிநோக்கிய திசையிலுள்ள ஓரலகு வெக்டராகும்.
• மின்னூட்டம் பெற்ற முடிவிலா சமதளத்தட்டினால் உருவாகும் மின்புலமானது மின்னூட்ட பரப்படர்த்தியைச் சார்ந்தும் அதேசமயம் தொலைவைச் சாராமலும் இருக்கின்றது.
• மின்னூட்டம் பெற்றத் தட்டிலிருந்து கணிசமான தொலைவிலுள்ள எந்தவொரு புள்ளியிலும் மின்புலம் சமமாக இருக்கும்.
• σ > 0 எனில் எந்தவொரு புள்ளியிலும் (P) மின்புலமானது தளத்திற்கு செங்குத்தாக இருக்கும்.
• σ < 0 எனில் மின்புலமானது தளத்திற்கு செங்குத்தாக உள்நோக்கிய திசையில் இருக்கும்.
13. மின்னூட்டம் சீராகப் பெற்ற ஒரு கோளகக் கூட்டினால் ஏற்படும் மின்புலத்திற்கான சமன்பாட்டைத் தருவிக்க.
• R ஆரமும் Q மின்னூட்டமும் கொண்ட, சீரான மின்துகள் பரவல் பெற்ற உள்ளீடற்ற கோளம் ஒன்றைக் கருதுவோம். காஸ் விதியைப் பயன்படுத்தி கோளத்திற்கு வெளியேயும் உள்ளேயும் உள்ள புள்ளிகளில் மின்புலத்தைக் கருதுவோம்.
• நேர்வு (அ) கோளத்திற்கு வெளியில் உள்ள புள்ளியில் (r > R)
• கோளத்தின் மையத்திலிருந்து r தொலைவில் கோளத்தின் வெளியே உள்ள புள்ளி P ஐக் கருதுவோம்.
• மின்துகள்கள் கோளத்தின் புறப்பரப்பில் சீராக பரவியுள்ளன (கோளகச் சமச்சீர் தன்மை). ஆகவே Q > 0 எனில் மின்புலம் ஆர வழியே வெளிநோக்கிய திசையிலும் Q < 0 எனில் ஆர உள்நோக்கிய திசையிலும் இருக்கிறது.
• r ஆரம் கொண்ட கோள வடிவ காஸியன் பரப்பினைக் கருதுவோம். இப்பரப்பினால் சூழப்படும் மின்துகள்களின் மொத்த மின்னூட்டம் Q என்க. காஸ் விதியைப் பயன்படுத்தி

• காஸியன் பரப்பின் அனைத்து புள்ளிகளிலும் மின்புலமும் ( ![]() ) பரப்பளவுக்கூறும் (
) பரப்பளவுக்கூறும் (![]() ) ஒரே திசையில் (வெளிநோக்கிய திசையில், செங்குத்தாக) அமைகின்றன.
) ஒரே திசையில் (வெளிநோக்கிய திசையில், செங்குத்தாக) அமைகின்றன.
• மின்துகள் நிலையமைப்பின் கோளகச் சமச்சீர் தன்மையால் கரஸியன்பரப்பில் உள்ள அனைத்து புள்ளிகளிலும் E ன் எண் மதிப்பும் சமமாகவே இருக்கும்.
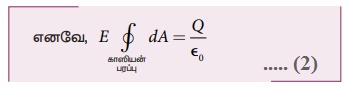


வெக்டர் வடிவில் 
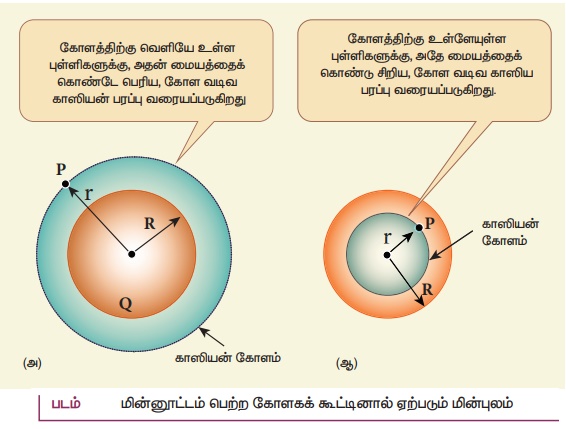
• நேர்வு (ஆ) : கோளத்தின் புறப்பரப்பில் உள்ள புள்ளியில் (r = R)
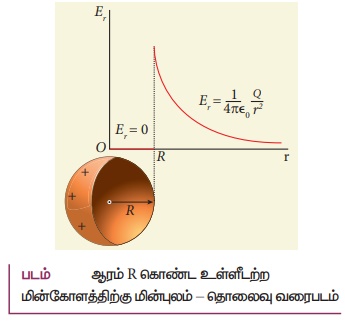
கோளகக் கூட்டின் புறப்பரப்பில் உள்ள புள்ளிகளுக்கு (r = R) மின்புலமானது.

• நேர்வு (இ) : கோளத்திற்கு உள்ளேயுள்ள புள்ளியில் (r < R)
• கோளகத்தின் மையத்திலிருந்து r தொலைவில், கோளத்திற்கு உள்ளேயுள்ள புள்ளி Pவைக் கருதுவோம். r ஆரம் கொண்ட கோள வடிவ காஸியன் பரப்பு ஒன்றை வரைவோம். (r < π)
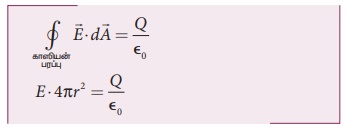
Q = 0
E = 0
14. நிலை மின் சமநிலையில் உள்ள கடத்திகளின் பல்வேறு பண்புகளை விவாதிக்கவும்.
(i) கடத்தியின் உட்புறத்திலிருக்கும் அனைத்து புள்ளிகளிலும் மின்புலம் சுழியாகும். இக்கூற்று திண்மக் கடத்தி மற்றும் உள்ளீடற்ற கூடு வகைக் கடத்தி இரண்டிற்கும் பொருந்தும்.
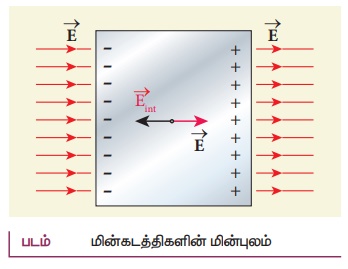
• புறமின்புலத்தை செயல்படுத்தும் முன் கடத்தியிலுள்ள கட்டுறா எலக்ட்ரான்கள் கடத்தி முழுவதிலும் சீராகப் பரவியிருக்கும்.
• மின்புலத்தை செயல்படுத்தும் போது, இடக்கைப் பக்கம் முடுக்கப்படுவதால் இடதுபக்கத் தகடு எதிர் மின்னூட்டமும், வலதுபக்கத் தகடு நேர் மின்னூட்டமும் பெறுகின்றன.
• கட்டுறா எலக்ட்ரான்கள் இவ்வாறு மீளமைவதால் கடத்தியின் உட்புறம் அக மின்புலம் உருவாகின்றது. புற மின்புலத்தை சமன் செய்யும் வரை இது அதிகரிக்கின்றது.
• புற மின்புலம் சமன் செய்யப்பட்ட பின்பு கடத்தி நிலை மின் சமநிலையிலுள்ளதாகக் கருதப்படுகிறது.
• இச்சமநிலையை அடைய ஒரு கடத்தி எடுத்துக்கொள்ளும் நேரம் ஏறக்குறைய 10−16S
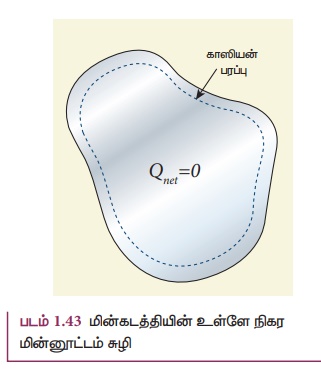
ii) கடத்தியின் உட்புறத்தில் உள்ள மின்துகள்களின் நிகர மின்னூட்டம் சுழி. கடத்திகளின் புறப்பரப்பில் மட்டுமே மின்துகள்கள் இருக்க முடியும்.
• ஏதேனும் ஒரு வடிவமுள்ள கடத்தி ஒன்றைக் கருதுவோம். கடத்தியின் புறப்பரப்பிற்கு வெகு அருகில், உட்புறமாக ஒரு காஸியன் பரப்பை வரைவோம்.
• காஸ் விதியின் படி, கடத்தியின் உட்புறம் இருக்கும் நிகர மின்னூட்ட மதிப்பும் சுழி என்பதையே இது உணர்த்துகிறது.
(iii) கடத்திக்கு வெளியே மின்புலமானது அதன் பரப்புக்கு செங்குத்தாகவும் σ/εo எண் மதிப்பு கொண்டதாகவும் இருக்கும். இங்கு σ என்பது கடத்தியின் குறிப்பிட்ட பகுதியில் உள்ள மின்னூட்டப் பரப்படர்த்தி ஆகும்.
• கடத்தியின் பரப்பிற்கு இணையான திசைகளில் மின்புலத்தின் கூறுகள் இருந்தால் பரப்பிலுள்ள கட்டுறா எலக்ட்ரான்கள் முடுக்கப்படும்.
• நிலைமின் சமநிலையில், கடத்தியின் பரப்புக்கு செங்குத்தான திசையில் மட்டுமே மின்புலம் அமையும்.
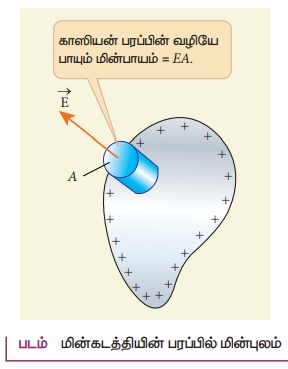
• சிறிய உருளை வடிவ காஸியன் பரப்பைக் கருதுவோம். உருளையின் ஒரு பாதி கடத்தியின் உட்புறமாகப் பதிந்துள்ளது.
• கடத்தியின் பரப்புக்கு செங்குத்தாக மின்புலத்தின் திசை இருக்கும் என்பதால், உருளையின் வளைபரப்பினைக் கடக்கும் மின்பாயம் சுழி.
• கடத்தியின் உட்புறம் மின்புலம் சுழியாகும்.
• மேல்பக்க தட்டைப் பரப்பு மட்டுமே மின்பாயத்தைக் கொடுக்கும்.
• மின்புலத்தின் திசையானது பரப்பு வெக்டரின் திசையிலேயே இருக்கும்.
• மேற்பாதி உருளையில் பரப்பிற்கு உட்புறம் உள்ள மின்துகள்களின் மொத்த மின்னூட்ட மதிப்பு …… σ A.
காஸ் விதியைப் பயன்படுத்த, EA = σA/ε0.

வெக்டர் வடிவில், 
(iv) கடத்தியின் புறப்பரப்பிலும் உட்புறத்திலும் நிலைமின்னழுத்தம் ஒரே மதிப்பு கொண்டிருக்கும்.
• பரப்பிலுள்ள அனைத்து புள்ளிகளிலும் மின்னழுத்தம் சமமாக இருக்க வேண்டும் அல்லது ஏதேனும் இரு புள்ளிகளுக்கு இடையேயுள்ள மின்னழுத்த வேறுபாடு சுழியாக இருக்க வேண்டும்.
• கடத்தியின் உட்புறம் மின்புலம் சுழியாதலால், கடத்தியின் புறப்பரப்பில் உள்ள மின்னழுத்தமும், உட்புறம் உள்ள மின்னழுத்தமும் சமமாக இருக்க வேண்டும்.
• நிலைமின் சமநிலையில் ஒரு கடத்தி எப்போதும் சமமின்னழுத்தத்தில் உள்ளது.
15. நிலை மின் தூண்டல் செயல்முறையை விவரிக்கவும்.
• தொடுதல் இன்றியே ஒரு பொருளை மின்னேற்றம் பெறச் செய்யும் நிகழ்வு நிலைமின் தூண்டல் எனப்படும்.
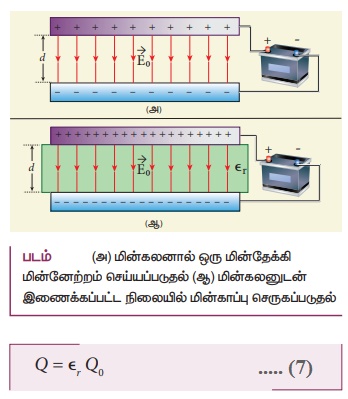
• மின்கடத்தாத் தாங்கி ஒன்றின் மீது வைக்கப்பட்டுள்ள மின்னூட்டமற்ற (மின் நடுநிலையான) கோள வடிவக் கடத்திப்பொருள் ஒன்றைக் கருதுவோம். எதிர் மின்னூட்டம் பெற்ற தண்டு ஒன்று கோளத்தின் அருகில், அதைத் தொடாதவாறு, கொண்டு வரப்படுகிறது. (படம் − அ)
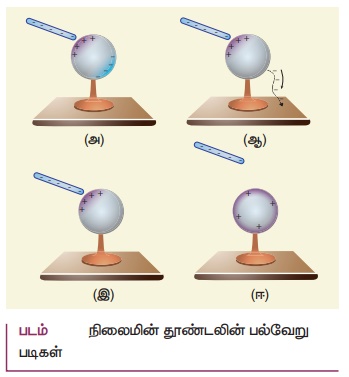
• தண்டிலுள்ள எதிர்மின்துகள் கடத்தியிலுள்ள எலக்ட்ரான்களை எதிர்ப்பக்கத்தை நோக்கி விரட்டுகிறது. இதன் விளைவாக, மின்னூட்டம் பெற்ற தண்டு இருக்கும் பக்கத்தில் நேர் மின்துகள்களும் அதற்கு எதிர்ப்பக்கத்தில் எதிர் மின்துகள்களும் தூண்டப்படுகின்றன.
• மின்னூட்டம் பெற்ற தண்டினைக் கொண்டு வருமுன், கடத்தியின் (கோளத்தின்) பரப்பு முழுவதும் கட்டுறா எலக்ட்ரான்கள் சீராகப் பரவியிருந்தன. மேலும் அதன் நிகர மின்னூட்டம் சுழியாக இருந்தது. ஆனால், தண்டினை கடத்தியினருகில் கொண்டு சென்றவுடன் எலக்ட்ரான்கள் தண்டிற்கு சேய்மைப் பக்கத்திலும் நேர் மின் துகள்கள் அண்மைப் பக்கத்திலுமாக அமைந்து, மின்துகள்களின் பரவல் சீரற்றதாகிறது. இருப்பினும், நிகர மின்னூட்டம் சுழியே.
• இப்போது கோளக்கடத்தியை ஒரு மின்கடத்துக் கம்பியின் மூலம் தரைக்கு இணைப்புக் கொடுக்கப்படுகிறது. இதற்கு தரையிணைப்பு (Grounding) என்று பெயர். எவ்வளவு எலக்ட்ரான்களை வேண்டுமானாலும் தரையால் (புவியால்) ஏற்றுக்கொள்ள முடியுமாதலால் கோளகக் கடத்தியிலுள்ள எலக்ட்ரான்கள் தரையிணைப்பினால் தரைக்குள் சென்று விடுகின்றன. ஆனால் கோளத்தில் உள்ள நேர்மின்துகள்கள் தண்டிலுள்ள எதிர்மின் துகள்களின் கவர்ச்சி விசைக்கு உட்பட்டுள்ளதால், இந்த நேர்மின்துகள்கள் தரைக்கு பாய இயலாது. (படம் − ஆ)
• இப்போது தரையிணைப்புக் கம்பியினை எடுத்துவிட, கோளத்திலுள்ள நேர் மின்துகள்கள் மின்னூட்டம் பெற்ற தண்டிற்கு அருகிலேயே உள்ளன. (படம் − இ)
• மின்னூட்டம் பெற்ற தண்டினை இப்போது கடத்தியிடமிருந்து அப்புறப்படுத்தி விடவும். அவ்வாறு அதனை நீக்கியவுடன் நேர் மின்துகள்கள் கடத்தியின் பரப்பில் சீராகப் பரவுகின்றன. இத்தகைய செயல்முறையின் மூலமாக மின்நடுநிலைத் தன்மை கொண்ட ஒரு கோள வடிவக் கடத்தி நேர் மின்னூட்டம் பெற்றதாக மாறுகிறது. (படம் − ஈ)
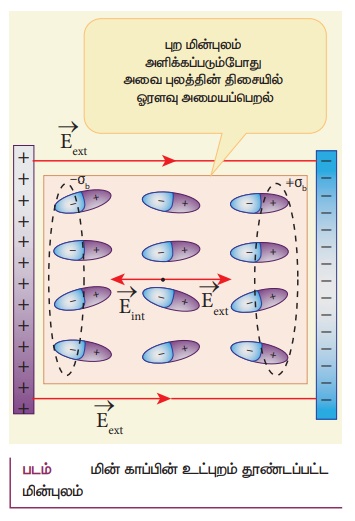
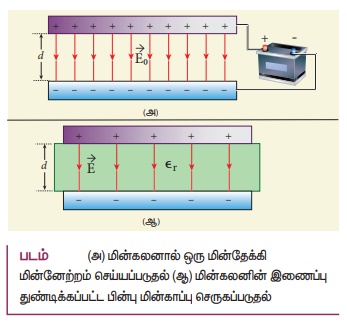
16. மின்காப்பை விளக்கி எவ்வாறு மின்காப்பினுள் மின்புலம் தூண்டப்படுகிறது என்பதையும் விளக்கவும்.
• கடத்தியொன்றைப் புற மின்புலத்தில் வைக்கும்போது, அதிலுள்ள மின்துகள்கள் ஒருங்கமைக்கப்பட்டு, அதனால் உருவாகும் அக மின்புலமானது புற மின்புலத்தை சமன் செய்யும்.
• ஆனால் மின்காப்பைப் பொருத்தவரை, அதில் கட்டுறா எலக்ட்ரான்கள் இல்லாததால், புற மின்புலமானது அதிலுள்ள மின்துகள்களை ஒருங்கமைக்கச் செய்தாலும் அதனால் உருவாகும் அக மின்புலம் புற மின்புலத்தை விடக் குறைவாக இருக்கும்.
• எனவே, மின்காப்பின் உட்புறம் நிகர மின்புலம் சுழியாவதில்லை , மேலும் புற மின்புலத்தின் திசையிலேயே நிகர மின்புலம் இருக்கிறது. ஆனால் அதன் எண்மதிப்பு புற மின்புலத்தைவிடக் குறைவாகவே இருக்கும்.
• மின்தேக்கி ஒன்றின் எதிரெதிர் மின்னூட்டம் பெற்ற இரு தட்டுகளுக்கு இடையே ஒரு செவ்வக வடிவ மின்காப்புப் பாளம் வைக்கப்படுகிறது.
• தட்டுகளுக்கு இடையே நிலவும் சீரான மின்புலம் மின்காப்பிற்கு ஒரு புற மின்புலமாக ![]() செயல்பட்டு அதனை முனைவாக்கம் செய்கிறது.
செயல்பட்டு அதனை முனைவாக்கம் செய்கிறது.
• அதன் ஒரு பக்கத்தில் நேர் மின்துகள்களும் மற்றொரு பக்கம் எதிர் மின்துகள்களும் தூண்டப்படுகின்றன. ஆனால் மின்காப்பின் உட்புறத்திலோ ஒரு சிறு பருமனில் கூட நிகர மின்னூட்டம் சுழியாக இருக்கின்றது.
• ஆகவே புற மின்புலத்தில் வைக்கப்பட்டுள்ள ஒரு மின்காப்பானது, மின்னூட்ட பரப்படர்த்தி +σb மற்றும் −σb கொண்ட, எதிரெதிர் மின்னூட்டம் பெற்ற இரு தட்டுகளுக்கு ஒப்பாகும்.
• இம்மின்துகள்கள் கட்டுண்ட மின்துகள்கள் (Bound charges) எனப்படும். இவை கடத்தியிலுள்ள கட்டுறா எலக்ட்ரான்களைப் போல் இவை தடையற்ற இயக்கத்தைப் பெற முடியாது.
17. இணைத்தட்டு மின்தேக்கியின் மின்தேக்குத் திறனுக்கான கோவையைப் பெறுக
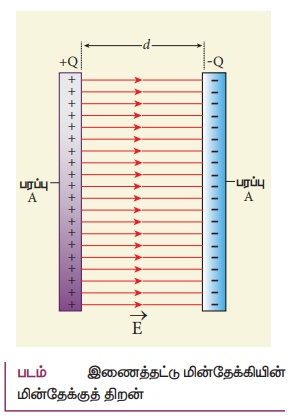
• குறுக்குவெட்டுப் பரப்பளவு A மற்றும் d இடைத்தொலைவினால் பிரித்து வைக்கப்பட்டுள்ள இரு இணைத்தட்டுகளைக் கொண்ட மின்தேக்கியைக் கருதுவோம்.
• இரு முடிவிலா இணைத் தட்டுகளுக்கிடையில் மின்புலம் சீராகவும் 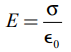 மதிப்பு கொண்டும் இருக்கும். இங்கு σ என்பது தட்டுகளின் மின்னூட்டப் பரப்படர்த்தி =
மதிப்பு கொண்டும் இருக்கும். இங்கு σ என்பது தட்டுகளின் மின்னூட்டப் பரப்படர்த்தி = 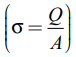
• தட்டுகளின் பரப்பளவைக் காட்டிலும் இடைத்தொலைவு d மிகவும் சிறியதாக இருப்பின் (d2<<A) வரம்பிற்குட்பட்ட அளவு கொண்ட (finite sized) இணைத்தட்டு மின் தேக்கிக்கும் கூட மேலே கூறப்பட்ட சமன்பாடு பொருந்தும்.
• எனவே தட்டுகளுக்கிடையேயான மின்புலம் 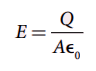
• மின்புலம் சீராக இருப்பதால், தட்டுகளுக்கு இடையேயான மின்னழுத்த வேறுபாடு

• எனவே மின்தேக்கியின் மின்தேக்குத்திறன்
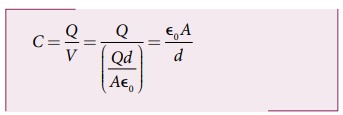
• மின்தேக்குத்திறன் தட்டின் குறுக்குவெட்டுப் பரப்பளவிற்கு நேர்த்தகவிலும் இரு தட்டுகளுக்கிடையேயுள்ள தொலைவிற்கு எதிர்த்தகவிலும் உள்ளது என்பதை அறியலாம்.
• மின்தேக்கித் தட்டுகளின் பரப்பளவை அதிகரித்தால் அதே மின்னழுத்த வேறுபாட்டில் இன்னும் அதிகளவு மின்துகள்களைப் பரவச் செய்ய இயலும். எனவே, மின்தேக்குத்திறனும் அதிகமாகும்.
• தட்டுகளுக்கு இடையே உள்ள தொலைவு d ஐக் குறைக்கும் போது, E மாறிலி ஆதலால், அவற்றுக்கு இடையேயான மின்னழுத்த வேறுபாடும் (V) குறையும்.
• மின்கலனின் இருமுனைகளுக்கு இடையேயான மின்னழுத்த வேறுபாடு அதிகமாக இருப்பதால், முனைகளின் மின்னழுத்த வேறுபாடும் தட்டுகளுக்கு இடையேயான மின்னழுத்த வேறுபாடும் சமமாகும் வரை மின்கலத்திலிருந்து தட்டுகளுக்கு மின்துகள்கள் பாயும்.
• தட்டிடைத் தொலைவைக் கூட்டும் போது, மின்தேக்கியின் மின்னழுத்த வேறுபாடும் கூடுவதால், இப்போது அது மின்கலனின் மின்னழுத்தத்தை விட அதிகமாக இருக்கும்.
.• இரு மின்னழுத்தங்களும் சமமாகும் வரை மின்தேக்கித் தட்டுகளிலிருந்து மின்கலனுக்கு மின்துகள்கள் பாயும்.
18. இணைத்தட்டு மின்தேக்கியினுள் சேமித்து வைக்கப்படும் ஆற்றலுக்கான சமன்பாட்டைப் பெறுக.
• மின்தேக்கியானது மின்துகள்களை மட்டுமல்ல, மின்னாற்றலையும் சேமிக்கும் ஒரு கருவியாகும்.
• மின்தேக்கி ஒன்று மின்கலனுடன் இணைக்கப்படும் போது, −Q மின்னூட்ட அளவுடைய எலக்ட்ரான்கள் அதன் ஒரு தட்டிலிருந்து இன்னொன்றுக்கு இடம்பெயர்கின்றன. இந்த மின்துகள் இடப்பெயர்வுக்கு தேவைப்படும் வேலையை மின்கலன் செய்கிறது.
• செய்யப்பட்ட இவ்வேலையே மின்தேக்கியில் நிலை மின்னழுத்த ஆற்றலாகச் சேமித்து வைக்கப்படுகிறது.
• V மின்னழுத்த வேறுபாட்டில் dQ அளவு (infinitesimal) மின்னூட்டம் கொண்ட மின்துகள்களை நகர்த்த செய்யப்படும் வேலை
dW = V dQ

• மின்தேக்கியை மின்னேற்றம் (charge) செய்யத் தேவைப்படும் மொத்த வேலை
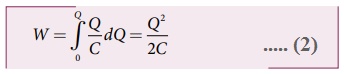
• இந்த வேலை நிலை மின்னழுத்த ஆற்றலாக (UE) மின்தேக்கியில் சேமிக்கப்படுகிறது.

இவ்வாறு சேமிக்கப்பட்ட ஆற்றலானது மின்தேக்குத் திறனுக்கும், தட்டுகளுக்கு இடையேயான மின்னழுத்த வேறுபாட்டின் இருமடிக்கும் நேர்த்தகவில் இருக்கின்றது. சமன்பாடு (3) பின்வருமாறு மாற்றி எழுதலாம். இங்கு.
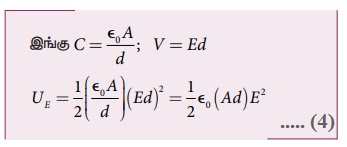
• இங்கு Ad = மின்தேக்கியின் தட்டுகளுக்கிடையே உள்ள பகுதியின் பருமன். இந்த இடைவெளிப் பகுதியின் ஓரலகு பருமனில் சேமிக்கப்பட்டுள்ள ஆற்றலை, நிலை மின்னழுத்த ஆற்றல் அடர்த்தி (UE) என வரையறுக்கலாம்.

• இதிலிருந்து, மின்தேக்கியின் தட்டுகளுக்கிடையே உள்ள இடைவெளியில் நிலவும் மின்புலத்தில்தான் ஆற்றல் சேமிக்கப்படுகிறது என்பதை அறிந்து கொள்ளலாம். மின்தேக்கியை மின்னிறக்கம் (discharge) செய்யும்போது ஆற்றல் திரும்பப் பெறப்படுகிறது.
• ஆற்றல் அடர்த்தியானது மின்புலத்தைச் சார்ந்து மட்டுமே உள்ளது. தட்டுகளின் அளவைப் பொறுத்து அது அமைவது இல்லை.
19. இணைத்தட்டு மின்தேக்கியினுள் மின்காப்பு வைக்கப்படுவதால் ஏற்படும் விளைவுகளை விரிவாக எழுதுக.
• A குறுக்கு வெட்டுப் பரப்பளவுடைய இணைத்தட்டுகள் d இடைவெளியில் பிரித்து வைக்கப்பட்டுள்ள மின்தேக்கி ஒன்றைக் கருதுவோம். V0 மின்னழுத்தமுடைய மின்கலனால் மின்தேக்கியானது Q0 மின்னூட்டம் கொண்ட மின்துகள்களை சேமிக்கும் அளவிற்கு மின்னேற்றம் செய்யப்படுகிறது. இந்நிலையில் மின்தேக்கியின் மின்தேக்குத்திறன்
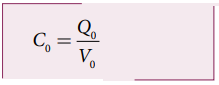
• மின்கலனுடனான இணைப்பைத் துண்டித்த பின்பு, தட்டுகளுக்கு இடையே மின்காப்பு நுழைக்கப்படுகிறது. மின்காப்பை நுழைத்த உடன் தட்டுகளுக்கிடையேயான மின்புலம் குறையும்.

• இங்கு E0 என்பது மின்காப்பு இல்லாத நிலையில் மின்தேக்கிக்கு இடையில் உள்ள மின்புலம் மற்றும், εr என்பது மின்காப்பின் சார்பு விடுதிறன் (relative permittivity) அல்லது மின்காப்பு மாறிலி எனப்படும். இங்கு εr > 1, என்பதால் E < Eo ஆகும்.
• இதன் விளைவாக, தட்டுகளுக்கிடையே உள்ள மின்னழுத்த வேறுபாடும் (V = Ed) குறையும். அதே சமயம், மின்கலனுடன் இணைப்பு இல்லாததால் தேக்கப்பட்ட மின்துகள்கள் எங்கும் செல்லாது. அதனால் மின்னூட்ட மதிப்பு QOம் மாறாது இருக்கும்.
• எனவே புதிய மின்னழுத்த வேறுபாடு,
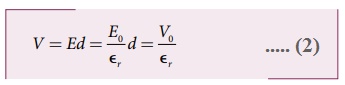
• மின்னழுத்த வேறுபாட்டிற்கு எதிர்த்தகவில் மின்தேக்குத்திறன் உள்ளதால், V குறைய C அதிகரிக்கும். மின்காப்பு உள்ள நிலையில் மின்தேக்குத்திறன்
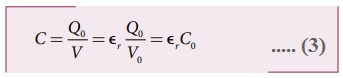
• εr > 1, ஆதலால் C > Co எனவே εr மாறிலியுடைய மின்காப்பைப் புகுத்திய பின்பு மின்தேக்குத்திறன் அதிகரிக்கின்றது. சமன்பாடு (3)ன் படி

ε = εrεo இங்கு ε என்பது மின்காப்பு ஊடகத்தின் விடுதிறன் எனப்படும்.
• மின்காப்பை நுழைக்கும் முன் மின்தேக்கியில் சேமிக்கப்பட்ட ஆற்றல்

• மின்காப்பு நுழைக்கப்பட்ட பின்பு, மின்னூட்டம் Q0 மாறாமலும் மின்தேக்குத்திறன் C அதிகரித்தும் காணப்படுவதால் சேமிக்கப்பட்ட ஆற்றலின் அளவு குறையும்.
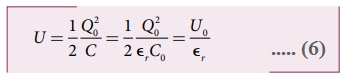
• εr > 1, ஆதலால் U < UO மின்காப்பைப் புகுத்தும்போது, அதை மின்தேக்கி உள்ளே இழுக்கிறது. இதற்காக சிறிது ஆற்றல் செலவிடப்படுவதாலேயே மின்தேக்கியின் ஆற்றல் அளவு குறைகின்றது.
(ii) மின்கலனுடன் இணைக்கப்பட்ட நிலையில் மின்தேக்கி
• தட்டுகளுக்கு இடையேயான மின்னழுத்த வேறுபாடு VO மாறாமல் இருக்கும். ஆனால் இந்நிலையில் மின்காப்பைப் புகுத்தினால் மின்தேக்கியில் சேமிக்கப்படும் மின்துகள்களின் அளவு εr மடங்காக உயரும், என்பதை ஆய்வுகளின் மூலம் (இதை முதலில் செய்து காட்டியவர் பாரடே) அறிகிறோம்.
• மின்துகள்களின் அளவு அதிகரிப்பதால், மின்தேக்குத்திறனும் அதிகரிக்கும். புதிய மின்தேக்குத்திறன்
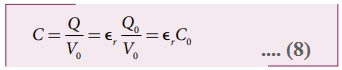
• எனினும்; மின்கலத்துடன் இணைக்கப்பட்ட நிலையிலுள்ள மின்தேக்கியின் மின்தேக்குத் திறன் அதிகரிப்பதற்கான காரணமும் மின்கலனுடன் இணைப்பு துண்டிக்கப்பட்ட நிலையிலுள்ள மின்தேக்கியின் மின்தேக்குத் திறன் அதிகரிப்பதற்கான காரணமும் வெவ்வேறு.

• மின்காப்பைப் புகுத்துவதற்கு முன் சேமிக்கப்பட்ட ஆற்றல்

• இங்கு 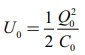 என்ற சமன்பாட்டை நாம் பயன்படுத்தாததைக் கவனிக்கவும். ஏனெனில் மின்துகள்களின் அளவும் மின்தேக்குத் திறனும் மாறுகின்ற இந்நேர்வில் V0 மட்டுமே மாறாமல் உள்ளது.
என்ற சமன்பாட்டை நாம் பயன்படுத்தாததைக் கவனிக்கவும். ஏனெனில் மின்துகள்களின் அளவும் மின்தேக்குத் திறனும் மாறுகின்ற இந்நேர்வில் V0 மட்டுமே மாறாமல் உள்ளது.
• மின்காப்பை நுழைத்தபின்பு, மின்தேக்குத்திறன் அதிகரிக்கிறது. இதனால் சேமிக்கப்பட்ட ஆற்றலும் அதிகரிக்கிறது.
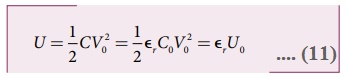
• மின்தேக்கியின் மின்னழுத்த வேறுபாடு VO மாறாமல் உள்ளதால் தட்டுகளுக்கிடையே நிலவும் மின்புலமும் மாறாமல் இருக்கும்.
ஆற்றல் அடர்த்தி 
இங்கு ε என்பது மின்காப்பு ஊடகத்தின் விடுதிறன் ஆகும்.
20. தொடரிணைப்பு மற்றும் பக்க இணைப்பில் மின்தேக்கிகள் இணைக்கப்படும் போது விளையும் தொகுபயன் மின்தேக்குத் திறனுக்கான சமன்பாடுகளைப் பெறுக.
தொடரிணைப்பில் மின்தேக்கிகள்:
• மின்னழுத்த வேறுபாடு V கொண்ட மின்கலனுடன் மூன்று மின்தேக்கிகள் தொடரிணைப்பில் உள்ளன. அவற்றின் மின்தேக்குத்திறன்கள் C1, C2 மற்றும் C3 மின்கலனின் மின் இணைப்பு கொடுக்கப்பட்டவுடன் C3 மின்தேக்கியின் வலது பக்கத் தட்டை நோக்கி −Q மின்னூட்ட அளவுடைய எலக்ட்ரான்கள் எதிர்மின் வாயிலிருந்து இடம் பெயர்கின்றன.
• இந்நிகழ்வுகளால் ஒவ்வொரு மின்தேக்கியிலும் சம அளவு மின்னூட்டம் Q கொண்ட மின்துகள்கள் சேமிக்கப்படுகிறது. மின்தேக்கிகளின் மின் தேக்குத்திறன் வெவ்வேறாக இருப்பதால் அவை ஒவ்வொன்றின் குறுக்கே நிலவும் மின்னழுத்த வேறுபாடும் வெவ்வேறாக இருக்கும். அவை முறையே V1,V2 மற்றும் V3 ஆகும்.
மின்தேக்கிகளின் குறுக்கே காணப்படும் மொத்த மின்னழுத்த வேறுபாடு, மின்கலனின் மின்னழுத்த வேறுபாட்டுக்குச் சமமாக இருக்க வேண்டும்.
V = V1 + V2 + V3

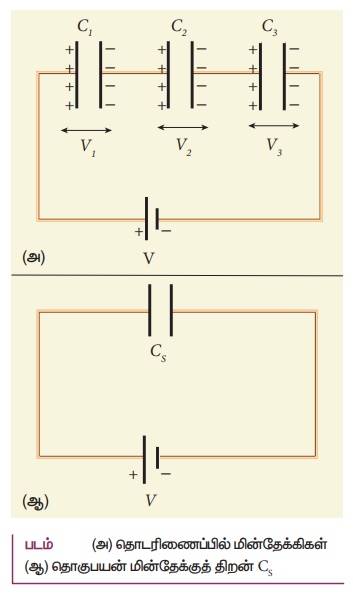
(அ) தொடரிணைப்பில் மின்தேக்கிகள்
(ஆ) தொகுபயன் மின்தேக்கு திறன் (Cs)
• தொடரிணைப்பிலுள்ள மூன்று மின்தேக்கிகளும் ஒரு தனித்த மின்தேக்கியை உருவாக்குவதாகக் கொண்டால்,
V = Q/CS சமன்பாடு (1) இல் பிரதியிட
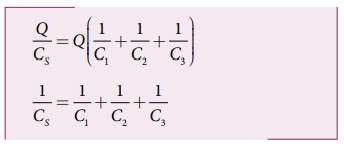
• எனவே, மின்தேக்கிகள் தொடரிணைப்பில் உள்ளபோது தொகுபயன் மின்தேக்குத்திறன் CS ன் தலைகீழ் மதிப்பானது ஒவ்வொரு மின்தேக்குத்திறனின் தலைகீழ் மதிப்புகளின் கூடுதலுக்குச் சமமாகும். தொகுபயன் மின்தேக்குத் திறனின் மதிப்பு CS ஆனது தொடரிணைப்பிலுள்ள மிகக்குறைந்த மின்தேக்குத் திறனை விட எப்போதும் குறைவாகவே இருக்கும்.
(ii) பக்க இணைப்பில் மின்தேக்கிகள்
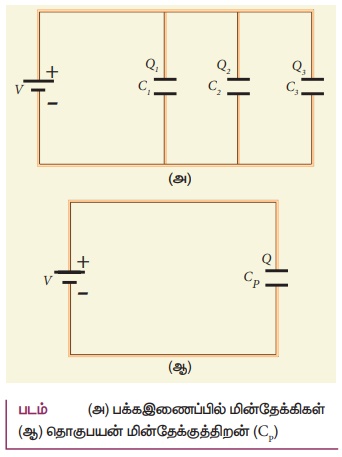
• மின்னழுத்த வேறுபாடு V கொண்ட மின்கலனுடன் மூன்று மின்தேக்கிகள் பக்க இணைப்பில் உள்ளன. அவற்றின் மின்தேக்குத்திறன்கள் C1, C2 மற்றும் C3.
• மின்தேக்கிகளின் ஒத்த பக்கங்கள் மின்கலனின் ஒரே நேர்முனை மற்றும் எதிர்மின் முனையுடன் இணைக்கப்பட்டு இருப்பதால், ஒவ்வொரு மின்தேக்கிக்குக் குறுக்கே தோன்றும் மின்னழுத்த வேறுபாடு சமமாகவும் அது மின்கலனின் மின்னழுத்த வேறுபாட்டுக்குச் சமமாகவும் இருக்கும்.
• ஒவ்வொரு மின்தேக்கியின் மின்தேக்குத்திறனும் வெவ்வேறாக இருப்பதால் அவற்றில் தேக்கப்படும் மின்துகள்களின் அளவுகளும் வெற்வேறாகவே இருக்கும். மின்தேக்கிகளில் சேமிக்கப்படும் மின்துகள் அளவுகள் முறையே Q1, Q2 மற்றும் Q3 என்க. மொத்த மின்னூட்ட மாறா விதியின் படி இம்மூன்று மின்துகள்களின் மின்னூட்டங்களின் கூடுதலானது மின் கலனிலிருந்து பெறப்பட்ட மின்துகள்களின் மின்னூட்டம் Q க்கு சமம் எனலாம்.
Q = Q1 + Q2 + Q3
Q = CV , என்பதால் Q = C1 V + C2 V + C3V
• இம்மூன்று மின்தேக்கிகளும் ஒரு தனித்த மின்தேக்கியை உருவாக்குவதாகக் கொண்டால், அதில் தேக்கப்படும் மின்னூட்டம் Q = CPV எனலாம்.
Cp V = C1 V + C2 V + C3V
Cp = C1 + C2 +C3
• மின்தேக்கிகள் பக்க இணைப்பில் உள்ளபோது அவற்றின் தொகுபயன் மின்தேக்குத்திறன் CP யானது தனித்தனி மின்தேக்கிகளின் மின்தேக்குத்திறன்களின் கூடுதலுக்குச் சமம்.
• தொகுபயன் மின்தேக்குத் திறனின் மதிப்பு பக்க இணைப்பிலுள்ள அதிகபட்ச தனித்த மின்தேக்குத்திறனை விட எப்போதும் அதிகமாகவே இருக்கும். பக்க இணைப்பிலுள்ள மின்தேக்கி ஒவ்வொன்றின் பரப்பளவையும் கூட்டும் போது கிடைக்கும் தொகுபயன் பரப்பளவு அதிகமாக உள்ளதால் அதன் தொகுபயன் மின்தேக்குத் திறனும் அதிகமாக உள்ளது.
21. ஒரு கடத்தியில் மின்துகள்களின் பரவலைப் பற்றி விரிவாக எழுதுக. மின்னல் கடத்தியின் தத்துவத்தை விளக்குக.
• ஆரங்கள் முறையே r1, r2 கொண்ட A, B என்ற இரு மின்கடத்து கோளங்கள் ஒரு மெல்லிய கடத்து கம்பியினால் ஒன்றோடொன்று இணைக்கப்பட்டுள்ளன.
• கோளங்களுக்கு இடைப்பட்ட தொலைவு அவற்றின் ஆரங்களை விட மிகவும் அதிகம் என வைக்கவும்.
• ஏதேனும் ஒரு கோளத்திற்கு Q அளவு மின்னூட்டம் கொண்ட மின்துகள்கள் அளிக்கப்படும் போது, இரு கோளங்களின் மின்னழுத்தமும் சமமாகும் வரை இம்மின்துகள்கள் இரு கோளங்களிலும் பரவுகின்றது.
• இப்போது கோளங்கள் சீரான மின்துகள் பரவலைப் பெறுவதால் நிலைமின் சமநிலையை அடைகின்றன. கோளம் Aன் பரப்பில் அமையும் மின்னூட்டம் q1 எனவும், கோளம் Bன் பரப்பில் அமையும் மின்னூட்டம் q2 எனவும் கொண்டால், Q = q1 + q2. கடத்திகளின் புறப்பரப்பிலேயே மின்துகள்கள் பரவியுள்ளன. மேலும் கடத்திகளின் உட்புறம் எவ்வித நிகர மின்னூட்டமும் இருக்காது.
• கோளம் A ன் பரப்பில் நிலை மின்னழுத்தம்

• கோளம் B ன் பரப்பில் நிலைமின்னழுத்தம்

• கடத்தியின் பரப்பு சம மின்னழுத்தத்தில் இருக்கும். மேலும் கோளங்கள் கடத்து கம்பியில் இணைக்கப்பட்டுள்ளதால் அவற்றின் பரப்புகள் இணைந்து ஒரே சம மின்னழுத்தப் பரப்பை உருவாக்குகின்றன.
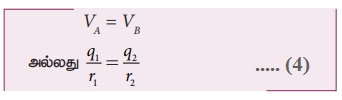
• கோளம் A ன் மின்னூட்டப் பரப்படர்த்தி σ1 எனவும் B ன் மின்னூட்டப் பரப்படர்த்தி σ2 எனவும் வைப்போம். இதிலிருந்து q1 = 4πr12σ1 மற்றும்
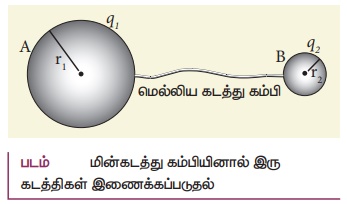
மின்னல் தாங்கி அல்லது மின்னல் கடத்தியின் தத்துவம்:
• கூர்முனைச் செயல்பாடு அல்லது ஒளிவட்ட மின்னிறக்கம்
விளக்கம்: வளைவு ஆரம் குறைவான பகுதிகளில் மின்னூட்ட பரப்படர்த்தி அதிகமாக இருக்கும் கடத்தியில் வளைவுத்தன்மை அதிகமுள்ள முனைகளில் மின்துகள்கள் அதிகமாக குவிவதால் மின்புலம் வலிமையுடன் உள்ளது.
• இது அப்பகுதியிலுள்ள காற்றை அயனியாக்கம் செய்கிறது. இப்போது கூர்முனைக்கு அருகிலுள்ள நேர்மின்துகள்கள் விரட்டப்படுகின்றன. எதிர்மின் துகள்கள் கூர்முனையை நோக்கி கவரப்படுகின்றன. இதனால் கடத்தியின் கூர்முனைப் பகுதியிலுள்ள மின்துகள்களின் மொத்த மின்னூட்ட மதிப்பு குறைகிறது. இதையே கூர்முனைச் செயல்பாடு அல்லது ஒளிவட்ட மின்னிறக்கம் என்பர்.
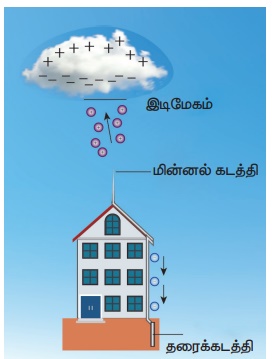
பயன்: உயரமான கட்டடங்களை மின்னல் வெட்டுகளிலிருந்து பாதுகாக்க உதவும் ஒரு கருவி மின்னல் கடத்தி.
அமைப்பு:
• இது கட்டத்தின் வழியே தரைக்குச் செல்லும் ஒரு நீண்ட, தடித்த தாமிரத் தண்டினைக் கொண்டுள்ளது. அதன் மேல் முனையில் கூர்முனையுடைய ஊசிகள் பொருத்தப்பட்டுள்ளன.
• தண்டின் கீழ் முனையானது அதிக ஆழத்தில் புதைக்கப்பட்டுள்ள தாமிரத் தட்டுடன் இணைக்கப்பட்டுள்ளது.
செயல்பாடு:
• எதிர் மின்னூட்டம் பெற்ற மேகம் கட்டடத்தின் மேல் செல்லும் போது, கடத்தியின் கூர்முனைகளில் நேர் மின்னூட்டம் தூண்டப்படுகிறது.
• கூர்முனைகளில் தூண்டப்படும் மின்துகள்களின் அடர்த்தி அதிகமாதலால் கூர்முனைச் செயல்பாடு நிகழ்கிறது. நேர் மின்னூட்டம் பெற்றுள்ள இந்த மின்துகள்கள் கூர்முனைகளுக்கு அருகிலுள்ள காற்று மூலக்கூறுகளை அயனியாக்கம் செய்கின்றன.
• இதன்மூலம் உருவாகும் நேர் மின்னூட்டங்கள் மேகத்திலுள்ள எதிர் மின்னூட்டத்தின் ஒரு பகுதியை சமன் செய்கிறது. கூர்முனைகளை நோக்கி விரட்டப்பட்ட எதிர் மின்துகள்கள், தாமிரத் தண்டின் வழியே புவியை நோக்கி செல்கின்றன.
• மின்னல் கடத்தி மின்னலைத் தடுப்பதில்லை. மாறாக தரையை நோக்கி மின்னலைத் திருப்புவதன் மூலம் கட்டடங்களைப் பாதுகாக்கிறது.
22. வான்டி கிராப் இயற்றியின் அமைப்பு மற்றும் வேலை செய்யும் விதத்தை விரிவாக விளக்கவும்.
• இக்கருவி 107V அளவிலான மின்னழுத்த வேறுபாட்டை உருவாக்கும்.
தத்துவம்: நிலைமின் தூண்டல் மற்றும் கூர்முனை.
அமைப்பு:
• மின்காப்பு பெற்ற தாங்கியின் மீது ஒரு பெரிய உள்ளீடற்ற மின்கடத்து கோளம் பொருத்தப்பட்டுள்ளது.
• கோளத்தின் நடுவில் 'B' என்ற கம்பியும் தாங்கியின் அடிப்பகுதியில் C என்ற கம்பியும் பொருத்தப்பட்டுள்ளது.
• பட்டுத் துணியால் ஆன பட்டை கப்பியின் வழியே செல்கிறது.
• கப்பி C மின்மோட்டார் மூலம் தொடர்ந்து இயக்கப்படுகிறது.
• கப்பிகளுக்கு அருகில் D மற்றும் E ஆகிய இரு சீப்பு வடிவ கடத்தி இணைக்கப்பட்டுள்ளன.
செயல்பாடு:
.• சீப்பு D அருகில் உள்ள காற்று உயர் மின்னழுத்தம் காரணமாக அயனியாக்கப்படுகிறது.
• நேர் மின்துகள்கள் பட்டையை நோக்கியும், எதிர் மின்துகள்கள் சீப்பு Dஐ நோக்கியும் நகர்கின்றன.
• அவை பட்டையில் ஒட்டிக்கொண்டு மேல்நோக்கி நகர்கின்றன.
• நிலைமின் தூண்டலை சீப்பு E எதிர் மின்னூட்டத்தையும், கோளம் நேர் மின்னூட்டத்தையும் பெறுகின்றன.
• அதே சமயம், கூர்முனை செயல்பாட்டால் பட்டையில் உள்ள எதிர்மின்னூட்டம் காற்றிலுள்ள எதிர்துகள்களால் சமன் செய்யப்படுகின்றன.
• பட்டை கீழிறங்கும் போது மின்னூட்டமற்ற தன்மையை அடைகிறது.
• மின்துகள்கள் ஏற்கப்படாத நிலை வரை கோளம் முழுவதும் மின்துகள் பரவும்.
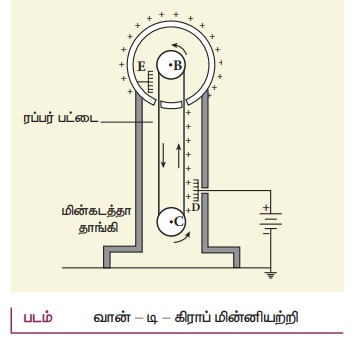
• மின்துகள் கசியாமலிருக்க உயர் அழுத்தத்தில் வாயு நிரப்பப்பட்ட எஃகு கலத்தில் கோளத்தினை மூட வேண்டும்.
பயன்கள்: உயர் மின்னழுத்த வேறுபாடு அணுக்கரு பிளவையில் பயன்படும் நேர்மின் அயனியை முடுக்கிவிக்க பயன்படுகிறது.