வடிவக் கணிதத்தில் ஓருறுப்புக் கோவைகளின் பெருக்கல்

வடிவக் கணிதத்தில் ஓருறுப்புக் கோவைகளின் பெருக்கல்

பெருக்கல் செயல்பாட்டைப் பல்வேறு வழிகளில் செய்ய முடியும் என்பதை நாம் ஏற்கனவே கற்றறிந்தோம். அவற்றுள் ஒன்றாகப் பெருக்கலை இரு பரிமாண உருவங்களின் பரப்பாகக் காணுதல்.

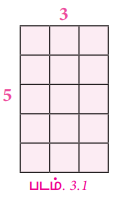
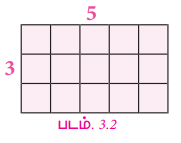
எடுத்துக்காட்டாக, 5×3 என்னும் பெருக்கலை, படம் 3.1 இல் உள்ளவாறு குறிக்கலாம். இந்தப் படத்திலுள்ள பெருக்கல் 5×3=15 ஆனது, 5 நிரைகள், 3 நிரல்களால் உருவான 15 சிறு சதுரங்களைக் குறிக்கிறது. படம் 3.2 லிருந்து, 5×3 என்னும் பெருக்கலும், 3×5 என்னும் பெருக்கலும் சமம் என்பது தெளிவாகிறது. (ஏனெனில், பெருக்கலானது பரிமாற்றுப் பண்புக்கு உட்பட்டது).

இங்கு பெருக்கலானது வலைப்பின்னல் மாதிரியால் விளக்கப்பட்டுள்ளது.

இதனைப் பரப்பைக் குறிக்கும் மாதிரியாகவும் பயன்படுத்தலாம். ஒரு வரிசைக்கு 5 சதுரம் வீதமாக, மூன்று வரிசைகள் உள்ளன. எனவே, 5×3 = 15. மேலும், 3×5 = 15 ஆகும்.

ஒரு பெரிய பரப்பை பல சிறிய பரப்புகளாகப் பிரிப்பதன் மூலம் பெருக்கலை நன்கு புரிந்துகொள்ளலாம். எடுத்துக்காட்டாக, மேற்கண்ட எடுத்துக்காட்டிலிருந்து செவ்வகத்தைப் பின்வருமாறு பிரிக்கலாம்.

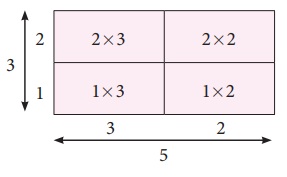
5×3 = (2×3) + (2×2) + (1×3) + (1×2)

= 6+4+3+2

= 15

இவ்வகையில், பகுப்பாய்வு மாதிரிகளைப் (decomposition model) பயன்படுத்தி, பெரிய எண்களின் பெருக்கலை எளிதில் காண இயலும்.

சிந்திக்க

நீள, அகலங்களைக் குறிக்கும் எண்களை ஒரே வழியில் மட்டும்தான் பிரிக்க இயலுமா? விவாதிக்க..

தீர்வு :  இல்லை  வெவ்வேறு வழிகளில் பிரிக்கலாம்  உதாரணமாக  15  1 × 15, 3 × 5, 5 × 3, 15 × 1

குறிப்பு 

பரப்பைக் குறிக்கும் மாதிரிகளை உருவாக்கும்போது, எண் அளவுகளுக்கேற்ப வரைய வேண்டியதில்லை. ஏனெனில் மாதிரிகள் கருத்தியல் நிலையையே குறிக்கிறது.

இந்தப் பெருக்கல் முறையின் நீட்சியாக மாறிகளின் பெருக்கலைக் காண்போம்.

நீளம் ‘x' ஆகவும், அகலம் 'y' ஆகவும் உள்ள செவ்வக வடிவ வில்லைகள் சிலவற்றைக் கருதுக. எனவே, ஒரு வில்லையின் பரப்பளவு xy ஆகும். அவற்றைப் படம் 3.3 இல் உள்ளவாறு அடுக்கி அதன் பரப்பளவைக் காண முயல்வோம்.

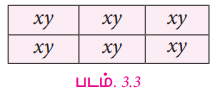
படம் 3.3 இல், 6 வில்லைகள் இணைந்து ஒரு செவ்வக வடிவத்தை உருவாக்குகிறது. ஒவ்வொரு வில்லையின் பரப்பளவும் xy ஆதலால், மொத்த உருவத்தின் பரப்பளவு 

6 × xy = 6xy  ...(1)

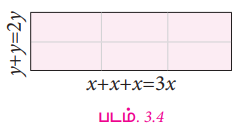
இதே செவ்வக உருவத்தின் நீளம் x+x+x=3x மற்றும் அகலம் y+y=2y எனக் கணக்கிடுவதன் மூலம் அதன் பரப்பளவைக் கண்டறியலாம். ஆகவே, அதன் பரப்பளவு = 3x × 2y   ………..(2)

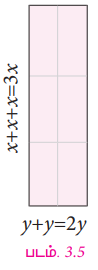
இப்போது, 6 வில்லைகளைப் படம் 3.5 இல் உள்ளவாறு மாற்றி அடுக்குவோம். புதிய செவ்வக உருவத்தின் நீளம் y+y=2y மற்றும் அகலம் x+x+x=3x எனில்,  அதன் பரப்பளவு = 2y × 3x   …………….(3)

சமன்பாடுகள்  (1), (2), (3) இலிருந்து அனைத்துப் பரப்புகளும் ஒரே உருவத்தைக் குறிப்பதனால், 6 xy = 3x × 2y = 2y × 3x.

வடிவக் கணிதம் மூலமாக 5×3 பெருக்கலை நாம் ஏற்கனவே கற்றுள்ளோம். இப்போது, இரண்டாம் எண் 3 இக்கு பதிலாக, 5 ஐப் பிரதியிட நமக்கு 5×5 கிடைக்கிறது.

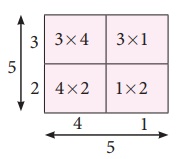
5×5 ஐக் கருதுக, வர்க்க எண் 52 =25 என்பதைப் பின்வருமாறு குறிக்கலாம். (மேலேயுள்ள படத்தைக் காண்க)

52 = (3×4) + (1×3) + (4×2) + (1×2)

= 12+3+8+2

=25 

படம் 3.5 இல் மாறிகளுக்கும் இதே போன்று நீட்சி செய்தால், அதாவது, 2y இக்கு பதிலாக 3x ஐப் பிரதியிட்டால், நீளமும் அகலமும் சமமாகி ஒரு சதுர வடிவம் கிடைக்கிறது.

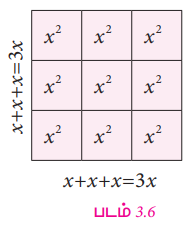
படம் 3.6 இல், பக்கங்கள் 3x மற்றும் சதுரத்தின் பரப்பளவு = 3x × 3x ………(4) 

மேலும், ஒரு வில்லையின் பரப்பளவு x2 என்பதுடன் ஒன்பது வில்லைகள் இருப்பதால், மொத்தச் சதுரத்தின் பரப்பு 9x2   ………(5) ஆகும்.

(4), (5) இலிருந்து இரு பரப்புகளும் சமம் என்பதால், 3x × 3x =9x2 எனக் கிடைக்கிறது. 

இப்போது, x மற்றும் (a+b) இன் பெருக்கற்பலனைக் காண்போம்.

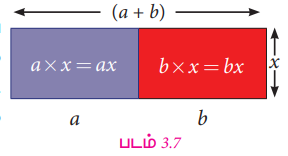
படம் 3.7 இலிருந்து இரு செவ்வகங்கள் இணைந்து ஒரு புதிய செவ்வகத்தை உருவாக்குகிறது. செவ்வகங்களின் அகலம் x மற்றும் அவற்றின் நீளங்கள் முறையே a மற்றும் b ஆகும். பெரிய செவ்வகத்தின் நீள, அகலம் முறையே (a+b) மற்றும் x எனக் கொண்டால்,

பெரிய செவ்வகத்தின் பரப்பு = செவ்வகம் 1 இன் பரப்பு + செவ்வகம் 2 இன் பரப்பு 

எனவே, (a+b) × x = (a × x) + (b × x)  (பங்கீட்டு பண்பு)

= ax + bx. 

ஆகவே, இரண்டு ஓருறுப்புக் கோவைகளின் பெருக்கலைப் பின்வருமாறு கருதலாம்.

1.  இரு ஓருறுப்புக் கோவைகளும் ஒரே மாறியை கொண்டிருக்கும் எனில்,

•  இரு ஓருறுப்புக் கோவைகளின் எண் கெழுக்களைத் தனியே பெருக்க வேண்டும். 

• ஒரே மாறியில் அமைந்த உறுப்புகளைப் பெருக்க, அடுக்கு விதியைப் பயன்படுத்த வேண்டும்.

am × an = am+n

குறிப்பு

ஓருறுப்புக் கோவைகளின் பெருக்கற்பலனும் ஓருறுப்புக் கோவையாகும்.

அதாவது, எடுத்துக்காட்டாக, x × x = x1 × x1 = x1+1 = x2.

மேலும் 3x2×2x3 = (3×2) (x2 × x3) =6 × ×2+3 = 6x5. 

2. வெவ்வேறு மாறிகளைக் கொண்ட ஓருறுப்புக் கோவைகளை பெருக்கும்போது, அந்த மாறிகளின் பெருக்கற்பலனாக எழுதவேண்டும். எடுத்துக்காட்டாக, 5x × 4y= (5×4) × (x × y) = 20xy.

இவற்றை முயல்க

1. பின்வரும் உருவங்களை உற்றுநோக்கி, வடிவக் கணிதம் முறையில், அவற்றின் பரப்பளவுகளைக் காண்க. மேலும், ஓருறுப்புக் கோவைகளின் பெருக்கலைப் பயன்படுத்தி, அவற்றைச் சரிபார்க்க.

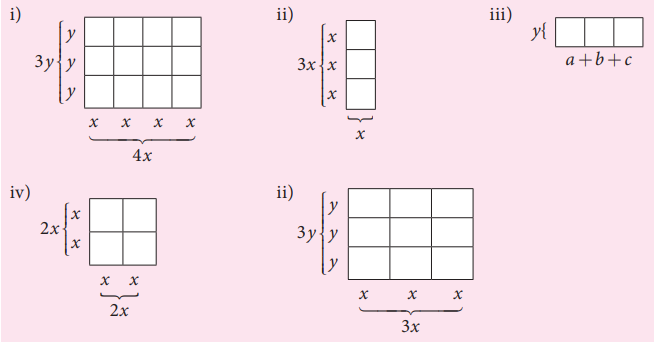
தீர்வு :

(i) பெட்டிகளின் பரப்பளவு   = xy

மொத்தம் 12 பெட்டிகள்

∴ மொத்த பரப்பளவு  = 12 × xy = 12xy

 நீளம் 4x மற்றும் அகலம்  3y ன் பெருக்கற்பலன்

செவ்வகத்தின் பரப்பளவு = 4x × 3y = 12xy

(ii) சிறிய பெட்டிகளின் பரப்பளவு = x2

மொத்தம் பெட்டிகள் = 3

∴ மொத்த பரப்பளவு = 3x2

செவ்வகத்தின் பரப்பளவு = 3x

செவ்வகத்தின் அகலம்  = x

செவ்வகத்தின் பரப்பளவு = நீளம் × அகலம்

= 3x × x

 = 3x2

(iii) சிறிய பெட்டிகளின் பகுதிகள்  ay, by, cy

∴ மொத்த பரப்பளவு = ay + by + cy = y (a + b + c)

செவ்வகத்தின் பரப்பளவு = நீளம் × அகலம்

 = (a + b + c) y

(iv) சிறிய சதுரத்தின் பரப்பளவு  = x2

 4 சிறிய சதுரங்கள் உள்ளன 

∴ கொடுக்கப்பட்ட சதுரத்தின்  மொத்த பரப்பளவு    = 4x2

பெரிய சதுரத்தின் பக்கம் = 2x

∴ சதுரத்தின் பரப்பளவு  = (2x)2 = 4x2

(v) சிறிய செவ்வகத்தின் பரப்பளவு  = xy

9 செவ்வகங்கள் உள்ளன 

∴ மொத்த பரப்பளவு = 9xy

பெரிய செவ்வகத்தின் பரப்பளவு  = நீளம் × அகலம்

= 3x × 3y = 9xy

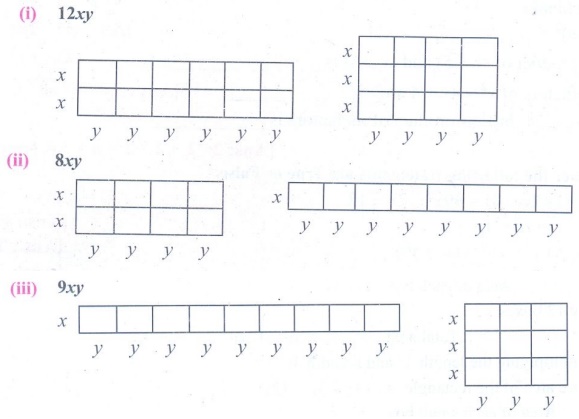
2. ஒரு செவ்வக வில்லையின் நீளத்தையும் அகலத்தையும் முறையே x மற்றும் y என்க. கீழ்க்கண்ட பரப்பளவுகள் கிடைக்கும் வகையில் உங்களால் முடிந்த எண்ணிக்கையில் செவ்வகங்களை உருவாக்கி அவற்றின் பக்க அளவுகளையும் குறிப்பிடுக.

(i) 12xy (ii) 8xy (iii) 9xy 

தீர்வு :