Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«»Я«▓Я»ЂЯ««Я»Ї Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«цЯ«ЋЯ«хЯ»ЂЯ««Я»Ї - Я«ЁЯ«▒Я«┐Я««Я»ЂЯ«ЋЯ««Я»Ї | 10th Mathematics : UNIT 8 : Statistics And Probability
10Я«хЯ«цЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ : Я«ЁЯ«▓Я«ЋЯ»Ђ 8 : Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«»Я«▓Я»ЂЯ««Я»Ї Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«цЯ«ЋЯ«хЯ»ЂЯ««Я»Ї
Я«ЁЯ«▒Я«┐Я««Я»ЂЯ«ЋЯ««Я»Ї
Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«»Я«▓Я»ЂЯ««Я»Ї Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«цЯ«ЋЯ«хЯ»ЂЯ««Я»Ї
Я«хЯ«ЙЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ѕЯ«»Я»Є Я«њЯ«░Я»Ђ Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«цЯ«ЋЯ«хЯ«┐Я«ЕЯ»Ї Я«ЋЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ««Я»ЇЯ«цЯ«ЙЯ«ЕЯ»Ї
-Я«хЯ«ЙЯ«▓Я»ЇЯ«ЪЯ«░Я»Ї Я«фЯ»ЄЯ«ЋЯ«ЙЯ«ЪЯ»Ї
Я«ЋЯ»іЯ«▓Я»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ«ЙЯ«хЯ«┐Я«▓Я»Ї Я«фЯ«┐Я«▒Я«еЯ»ЇЯ«ц Я«фЯ«┐Я«░Я«џЯ«еЯ»ЇЯ«ц Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«░ Я««Я«ЋЯ«▓Я»єЯ«ЕЯ»ІЯ«фЯ«┐Я«ИЯ»Ї Я«ЊЯ«░Я»Ї Я«ЄЯ«еЯ»ЇЯ«цЯ«┐Я«»Я«фЯ»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«▓Я«ЙЯ«│Я«░Я»Ї Я«єЯ«хЯ«ЙЯ«░Я»Ї. Я«ЄЯ«░Я»Ђ Я«цЯ«░Я«хЯ»ЂЯ«цЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ѕЯ«»Я»Є Я«ЅЯ«│Я»ЇЯ«│ Я«њЯ«фЯ»ЇЯ«фЯ»ЂЯ««Я»ѕ Я«ЁЯ«│Я«хЯ»ђЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ»ЇЯ«ЪЯ«▒Я«┐Я«»Я»ЂЯ««Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»ѕ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ«ЙЯ«░Я»Ї. Я«ЁЯ«цЯ«┐Я«ЋЯ«│Я«хЯ«┐Я«▓Я«ЙЯ«Е Я««Я«ЙЯ«цЯ«┐Я«░Я«┐ Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»єЯ«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕ Я««Я»ЄЯ«▒Я»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«│Я«фЯ»Ї Я«фЯ»ЂЯ«цЯ«┐Я«» Я«хЯ«┤Я«┐Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»ѕ Я«ЁЯ«▒Я«┐Я««Я»ЂЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ«ЙЯ«░Я»Ї. Я«џЯ««Я«хЯ«ЙЯ«»Я»ЇЯ«фЯ»ЇЯ«фЯ»Ђ Я««Я«ЙЯ«цЯ«┐Я«░Я«┐ Я««Я»ЂЯ«▒Я»ѕЯ«»Я»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«еЯ«┐Я«▓Я«фЯ»ЇЯ«фЯ«░Я«фЯ»ЇЯ«фЯ»ЂЯ«фЯ»ЇЯ«фЯ«»Я«┐Я«░Я»Ї Я«ЅЯ«▒Я»ЇЯ«фЯ«цЯ»ЇЯ«цЯ«┐ Я«ЁЯ«│Я«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ЂЯ««Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»ѕ Я«хЯ«┤Я«ЎЯ»ЇЯ«ЋЯ«┐Я«ЕЯ«ЙЯ«░Я»Ї. Я«ЄЯ«хЯ«░Я»ЂЯ«ЪЯ»ѕЯ«» Я«ЁЯ«│Я«фЯ»ЇЯ«фЯ«░Я«┐Я«» Я«фЯ«БЯ«┐Я«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Ћ, Я«ЄЯ«еЯ»ЇЯ«цЯ«┐Я«» Я«ЁЯ«░Я«џЯ«┐Я«ЕЯ»Ї Я««Я«┐Я«Ћ Я«ЅЯ«»Я«░Я«┐Я«» Я«хЯ«┐Я«░Я»ЂЯ«цЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«Е Я«фЯ«цЯ»ЇЯ««Я«хЯ«┐Я«фЯ»ѓЯ«иЯ«ЕЯ»Ї Я«хЯ«┐Я«░Я»ЂЯ«цЯ»Ђ 1968 Я«єЯ««Я»Ї Я«єЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«ЄЯ«еЯ»ЇЯ«цЯ«┐Я«» Я«ЁЯ«░Я«џЯ«ЙЯ«▓Я»Ї Я«хЯ«┤Я«ЎЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»Ђ. Я«ЄЯ«еЯ»ЇЯ«цЯ«┐Я«» Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«»Я«▓Я»Ї Я«цЯ»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЄЯ«хЯ«░Я»Ї Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«цЯ»ЇЯ«цЯ«┐Я«» Я«џЯ«ЙЯ«цЯ«ЕЯ»ѕЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Ћ "Я«ЄЯ«еЯ»ЇЯ«цЯ«┐Я«»Я«фЯ»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«»Я«▓Я«┐Я«ЕЯ»Ї Я«цЯ«еЯ»ЇЯ«цЯ»ѕ" Я«јЯ«ЕЯ«фЯ»Ї Я«фЯ»ІЯ«▒Я»ЇЯ«▒Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«ЙЯ«░Я»Ї. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я«ЄЯ«хЯ«░Я«цЯ»Ђ Я«фЯ«┐Я«▒Я«еЯ»ЇЯ«ц Я«еЯ«ЙЯ«│Я«ЙЯ«Е Я«юЯ»ѓЯ«ЕЯ»Ї Я««Я«ЙЯ«цЯ««Я»Ї 29-Я«єЯ««Я»Ї Я«цЯ»ЄЯ«цЯ«┐Я«»Я»ѕ Я«њЯ«хЯ»ЇЯ«хЯ»ІЯ«░Я»Ї Я«єЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«цЯ»ЄЯ«џЯ«┐Я«»Я«фЯ»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«»Я«▓Я»Ї Я«цЯ«┐Я«ЕЯ««Я«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«ЙЯ«ЪЯ»ЂЯ««Я»ЇЯ«фЯ«ЪЯ«┐ Я«ЄЯ«еЯ»ЇЯ«цЯ«┐Я«» Я«ЁЯ«░Я«џЯ«ЙЯ«ЎЯ»ЇЯ«ЋЯ««Я»Ї Я«ЁЯ«▒Я«┐Я«хЯ«┐Я«цЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ.

Я«ЋЯ«▒Я»ЇЯ«▒Я«▓Я»Ї Я«хЯ«┐Я«│Я»ѕЯ«хЯ»ЂЯ«ЋЯ«│Я»Ї
┬и Я««Я»ѕЯ«»Я«фЯ»Ї Я«фЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЁЯ«│Я«хЯ»ѕЯ«ЋЯ«│Я»ѕ Я«еЯ«┐Я«ЕЯ»ѕЯ«хЯ»Ђ Я«ЋЯ»ѓЯ«░Я»ЇЯ«цЯ«▓Я»Ї.
┬и Я«цЯ»іЯ«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ, Я«цЯ»іЯ«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ«ЙЯ«ц Я«хЯ«┐Я«хЯ«░Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«еЯ«┐Я«ЕЯ»ѕЯ«хЯ»Ђ Я«ЋЯ»ѓЯ«░Я»ЇЯ«цЯ«▓Я»Ї.
┬и Я«фЯ«░Я«хЯ«▓Я«┐Я«ЕЯ»Ї Я«ЋЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ»ЂЯ«░Я«┐Я«еЯ»ЇЯ«цЯ»Ђ Я«ЋЯ»іЯ«│Я»ЇЯ«│Я»ЂЯ«цЯ«▓Я»Ї.
┬и Я«хЯ»ђЯ«џЯ»ЇЯ«џЯ»Ђ, Я«цЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«хЯ«┐Я«▓Я«ЋЯ»ЇЯ«ЋЯ««Я»Ї, Я«хЯ«┐Я«▓Я«ЋЯ»ЇЯ«Ћ Я«хЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я«ЙЯ«▒Я»ЂЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»єЯ«┤Я»Ђ Я«єЯ«ЋЯ«┐Я«»Я«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ЂЯ«цЯ«▓Я»ѕЯ«фЯ»Ї Я«фЯ»ЂЯ«░Я«┐Я«еЯ»ЇЯ«цЯ»Ђ Я«ЋЯ»іЯ«│Я»ЇЯ«│Я«▓Я»Ї.
┬и Я«џЯ««Я«хЯ«ЙЯ«»Я»ЇЯ«фЯ»ЇЯ«фЯ»ЂЯ«џЯ»Ї Я«џЯ»ІЯ«цЯ«ЕЯ»ѕЯ«ЋЯ«│Я»Ї, Я«ЋЯ»ѓЯ«▒Я»ЂЯ«хЯ»єЯ«│Я«┐ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я«░Я«хЯ«░Я»ѕЯ«фЯ«ЪЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ Я«єЯ«ЋЯ«┐Я«»Я«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«фЯ»Ї Я«фЯ»ЂЯ«░Я«┐Я«еЯ»ЇЯ«цЯ»Ђ Я«ЋЯ»іЯ«│Я»ЇЯ«│Я«▓Я»Ї.
┬и Я«џЯ««Я«хЯ«ЙЯ«»Я»ЇЯ«фЯ»ЇЯ«фЯ»ЂЯ«џЯ»Ї Я«џЯ»ІЯ«цЯ«ЕЯ»ѕЯ«»Я«┐Я«ЕЯ»Ї Я«фЯ«▓Я»ЇЯ«хЯ»ЄЯ«▒Я»Ђ Я«хЯ«ЋЯ»ѕЯ«»Я«ЙЯ«Е Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ«│Я»ѕ Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«цЯ»ЇЯ«цЯ«▓Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«хЯ«┐Я«│Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ«▓Я»Ї.
┬и Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«цЯ«ЋЯ«хЯ»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«▓Я»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ»ЂЯ«░Я«┐Я«еЯ»ЇЯ«цЯ»Ђ Я«ЋЯ»іЯ«│Я»ЇЯ«│Я»ЂЯ«цЯ«▓Я»Ї. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ»ѕЯ«џЯ»Ї Я«џЯ«┐Я«▓ Я«јЯ«│Я«┐Я«» Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»ѕЯ«цЯ»Ї Я«цЯ»ђЯ«░Я»ЇЯ«фЯ»ЇЯ«фЯ«цЯ«▒Я»ЇЯ«ЋЯ»ЂЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«цЯ«▓Я»Ї
Я«ЁЯ«▒Я«┐Я««Я»ЂЯ«ЋЯ««Я»Ї (Introduction)
Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«»Я«▓Я»Ї (statistics) Я«јЯ«ЕЯ»ЇЯ«▒ Я«хЯ«ЙЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ»ѕЯ«»Я«ЙЯ«ЕЯ«цЯ»Ђ Я«ЄЯ«▓Я«цЯ»ЇЯ«цЯ»ђЯ«ЕЯ»Ї Я««Я»іЯ«┤Я«┐Я«»Я«┐Я«ЕЯ»Ї 'Я«еЯ«┐Я«▓Я»ѕЯ««Я»ѕРђЎ (status) Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ Я«ЁЯ«░Я«џЯ«┐Я«»Я«▓Я»Ї Я«еЯ«┐Я«▓Я»ѕЯ««Я»ѕ (political status) Я«јЯ«ЕЯ»ЇЯ«▒ Я«хЯ«ЙЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«хЯ«еЯ»ЇЯ«цЯ«цЯ»Ђ. Я«ЄЯ«ЕЯ»ЇЯ«▒Я»Ђ, Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«»Я«▓Я«ЙЯ«ЕЯ«цЯ»Ђ Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»ЂЯ«хЯ«░Я»ЂЯ«ЪЯ»ѕЯ«» Я«хЯ«ЙЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ѕЯ«»Я«┐Я«▓Я»ЂЯ««Я»Ї Я«јЯ«цЯ«┐Я«░Я»ЇЯ«ЋЯ«ЙЯ«▓Я«цЯ»Ї Я«цЯ«┐Я«ЪЯ»ЇЯ«ЪЯ««Я«┐Я«ЪЯ»ЂЯ«цЯ«▓Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ, Я«хЯ«┐Я«»Я«ЙЯ«фЯ«ЙЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ, Я«џЯ«еЯ»ЇЯ«цЯ»ѕ Я«єЯ«░Я«ЙЯ«»Я»ЇЯ«џЯ»ЇЯ«џЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»Ђ, Я«фЯ»іЯ«░Я»ЂЯ«│Я«ЙЯ«цЯ«ЙЯ«░ Я«ЁЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕ Я«цЯ«»Я«ЙЯ«░Я«┐Я«фЯ»ЇЯ«фЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я«јЯ«ЕЯ«фЯ»Ї Я«фЯ«▓ Я«џЯ»ѓЯ«┤Я«▓Я»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я«фЯ»Ї Я«фЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«хЯ«ЋЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я«ЋЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ«БЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«єЯ«┤Я««Я«ЙЯ«Е Я«єЯ«»Я»ЇЯ«хЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«»Я«▓Я»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я«┐Я«»Я«▓Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЁЯ«▒Я«┐Я«хЯ«┐Я«»Я«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐Я«цЯ»Ї Я«цЯ«░Я«хЯ»ЂЯ«ЋЯ«│Я»ѕЯ«џЯ»Ї Я«џЯ»ЄЯ«ЋЯ«░Я«┐Я«цЯ»ЇЯ«цЯ«▓Я»Ї, Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ««Я»ѕЯ«цЯ»ЇЯ«цЯ«▓Я»Ї, Я«цЯ»іЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«▓Я»Ї, Я«хЯ«┤Я«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ«▓Я»Ї, Я«фЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«ЙЯ«»Я»ЇЯ«хЯ»Ђ Я«џЯ»єЯ«»Я»ЇЯ«цЯ«▓Я»Ї, Я«ЁЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ««Я»ЂЯ«│Я»ЇЯ«│ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«ЋЯ«│Я»ѕ Я«ЈЯ«▒Я»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«цЯ«▓Я»Ї Я«єЯ«ЋЯ«┐Я«»Я«хЯ»ѕЯ«ЋЯ«│Я»ѕ Я«ЅЯ«│Я»ЇЯ«│Я«ЪЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я«цЯ»Ђ Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«џЯ»єЯ«ЕЯ»ЇЯ«▒ Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї, Я«цЯ«░Я«хЯ»ЂЯ«ЋЯ«│Я»ѕЯ«џЯ»Ї Я«џЯ»ЄЯ«ЋЯ«░Я«┐Я«цЯ»ЇЯ«цЯ«▓Я»Ї, Я«ЁЯ«ЪЯ»ЇЯ«ЪЯ«хЯ«БЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«цЯ«▓Я»Ї, Я«хЯ«░Я»ѕЯ«фЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«цЯ»ЇЯ«цЯ«▓Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЁЯ«│Я«хЯ»ѕЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я«єЯ«ЋЯ«┐Я«»Я«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«▒Я»ЇЯ«▒Я»ІЯ««Я»Ї. Я«цЯ«▒Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«ЄЯ«еЯ»ЇЯ«ц Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї, Я«фЯ«░Я«хЯ«▓Я»Ї Я«ЁЯ«│Я«хЯ»ѕЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«ЋЯ«▒Я»ЇЯ«фЯ»ІЯ««Я»Ї.
Я«еЯ«┐Я«ЕЯ»ѕЯ«хЯ»Ђ Я«ЋЯ»ѓЯ«░Я»ЇЯ«цЯ«▓Я»Ї
Я««Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЁЯ«│Я«хЯ»ѕЯ«ЋЯ«│Я»Ї
Я««Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЁЯ«│Я«хЯ»ѕЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я««Я»ЂЯ«┤Я»ЂЯ«фЯ»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«┐Я«хЯ«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ«ЋЯ»ЇЯ«ЋЯ«цЯ«ЙЯ«Е Я«њЯ«░Я»Ђ Я«цЯ«ЕЯ«┐ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ђЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«јЯ«БЯ»ЇЯ«БЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«еЯ»ЇЯ«ц Я«јЯ«БЯ»ЇЯ«БЯ»ѕ Я««Я»ѕЯ«»Я«фЯ»Ї Я«фЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЁЯ«│Я«хЯ»Ђ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«ЋЯ»ѓЯ«▒Я«▓Я«ЙЯ««Я»Ї.
Я«хЯ«┤Я«ЋЯ»ЇЯ«ЋЯ««Я«ЙЯ«Ћ Я««Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЁЯ«│Я«хЯ»ѕЯ«ЋЯ«│Я»Ї Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«┐Я«хЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ѕЯ«» Я«ЁЯ«│Я«хЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«еЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ««Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«┐Я«хЯ«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«фЯ«▓Я»ЇЯ«хЯ»ЄЯ«▒Я»Ђ Я«хЯ«ЋЯ»ѕЯ«»Я«ЙЯ«Е Я««Я»ѕЯ«»Я«фЯ»ЇЯ«фЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЁЯ«│Я«хЯ»ѕЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЙЯ«ЕЯ«хЯ»ѕ,
(i) Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐
(ii) Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕ Я«ЁЯ«│Я«хЯ»Ђ
(ii) Я««Я»ЂЯ«ЋЯ«ЪЯ»Ђ
Я«џЯ«┐Я«еЯ»ЇЯ«цЯ«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«│Я««Я»Ї
1. Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«хЯ«┐Я«хЯ«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐, Я«ЄЯ«ЪЯ»ѕЯ«еЯ«┐Я«▓Я»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я»ЂЯ«ЋЯ«ЪЯ»Ђ Я«єЯ«ЋЯ«┐Я«»Я«хЯ»ѕ Я«њЯ«░Я»Є Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«Й?
2. Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»ЇЯ«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«»Я»ЄЯ«»Я«ЙЯ«Е Я«хЯ«┐Я«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«џЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«Е?
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ
Рђб Я«цЯ«░Я«хЯ»Ђ : Я«њЯ«░Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«цЯ»Ї Я«цЯ«ЋЯ»ЂЯ«еЯ»ЇЯ«ц Я«јЯ«БЯ»ЇЯ«БЯ«│Я«хЯ«┐Я«▓Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЂЯ«хЯ«цЯ»ѕЯ«цЯ»Ї Я«цЯ«░Я«хЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї.
Рђб Я«цЯ«░Я«хЯ»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ : Я«цЯ«░Я«хЯ«┐Я«ЕЯ»Ї Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«цЯ«░Я«хЯ»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«јЯ«ЕЯ»ЇЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї.
Рђб Я««Я«ЙЯ«▒Я«┐ : Я«ЊЯ«░Я»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»єЯ«ЪЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«│Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«ЁЯ«│Я«хЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я«ЙЯ«▒Я«┐Я«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я««Я«ЙЯ«▒Я«┐Я«ЋЯ«│Я»Ї Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЙЯ«Ћ xi, i=1,2,3,Рђд,n Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е.
Рђб Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«хЯ»єЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї : Я«њЯ«░Я»Ђ Я«цЯ«░Я«хЯ«┐Я«▓Я»Ї, Я«њЯ«░Я»Ђ Я««Я«ЙЯ«▒Я«┐ Я«јЯ«хЯ»ЇЯ«хЯ«│Я«хЯ»Ђ Я««Я»ЂЯ«▒Я»ѕ Я«хЯ«░Я»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»І, Я«ЁЯ«еЯ»ЇЯ«ц Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕЯ«»Я»ѕ Я«еЯ«ЙЯ««Я»Ї Я««Я«ЙЯ«▒Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«хЯ»єЯ«БЯ»Ї Я«јЯ«ЕЯ»ЇЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї.
Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЙЯ«Ћ Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«хЯ»єЯ«БЯ»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ fi, i=1,2,3,Рђд,n. Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ.
Я«ЄЯ«еЯ»ЇЯ«ц Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я»ѕ Я«еЯ«┐Я«ЕЯ»ѕЯ«хЯ»Ђ Я«ЋЯ»ѓЯ«░Я»ЇЯ«хЯ»ІЯ««Я»Ї.
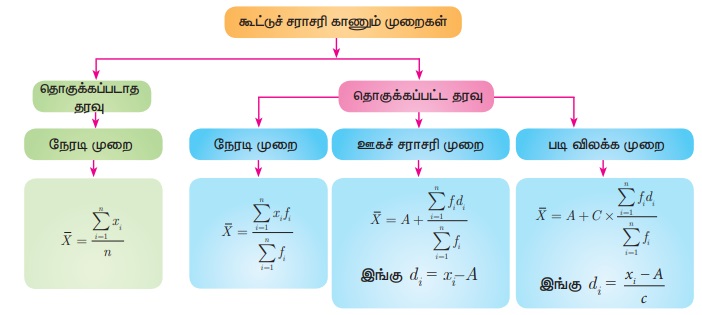
Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐
Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«цЯ«░Я«хЯ»ЂЯ«фЯ»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»ѕ Я«цЯ«░Я«хЯ»ЂЯ«фЯ»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕЯ«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«хЯ«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»ІЯ«цЯ»Ђ Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ»ѕ ![]() Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЂЯ«хЯ»ІЯ««Я»Ї (x Я«фЯ«ЙЯ«░Я»Ї Я«јЯ«Е Я«ЅЯ«џЯ»ЇЯ«џЯ«░Я«┐Я«фЯ»ЇЯ«фЯ»ІЯ««Я»Ї)
Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЂЯ«хЯ»ІЯ««Я»Ї (x Я«фЯ«ЙЯ«░Я»Ї Я«јЯ«Е Я«ЅЯ«џЯ»ЇЯ«џЯ«░Я«┐Я«фЯ»ЇЯ«фЯ»ІЯ««Я»Ї)

Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ђЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│ Я«цЯ«ЋЯ«хЯ«▓Я»ЇЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ»іЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ»Ђ Я«ЈЯ«▒Я»ЇЯ«▒ Я«џЯ»ѓЯ«цЯ»ЇЯ«цЯ«┐Я«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«еЯ«ЙЯ««Я»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«хЯ»ІЯ««Я»Ї.
Я«џЯ«┐Я«еЯ»ЇЯ«цЯ«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«│Я««Я»Ї
n Я«цЯ«░Я«хЯ»ЂЯ«фЯ»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я«ЙЯ«ЕЯ«цЯ»Ђ ![]() Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЪЯ«ЕЯ»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я»ѕЯ«»Я»ЂЯ««Я»Ї, Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«ЙЯ««Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЪЯ«ЕЯ»Ї Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«┐ Я«јЯ«Е Я«ЄЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Є Я«фЯ»ІЯ«ЕЯ«ЙЯ«▓Я»Ї Я«фЯ»ЂЯ«цЯ«┐Я«» Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«јЯ«ЕЯ»ЇЯ«ЕЯ«хЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї?
Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЪЯ«ЕЯ»Ї Я«њЯ«ЕЯ»ЇЯ«▒Я»ѕЯ«»Я»ЂЯ««Я»Ї, Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ«ЙЯ««Я»Ї Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЪЯ«ЕЯ»Ї Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«┐ Я«јЯ«Е Я«ЄЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»Ђ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Є Я«фЯ»ІЯ«ЕЯ«ЙЯ«▓Я»Ї Я«фЯ»ЂЯ«цЯ«┐Я«» Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«јЯ«ЕЯ»ЇЯ«ЕЯ«хЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї?
Я««Я»ЂЯ«ЕЯ»ЇЯ«ЕЯ»ЄЯ«▒Я»ЇЯ«▒Я«џЯ»Ї Я«џЯ»ІЯ«цЯ«ЕЯ»ѕ
1. Я«јЯ«▓Я»ЇЯ«▓Я«ЙЯ«цЯ»Ї Я«цЯ«░Я«хЯ»ЂЯ«фЯ»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«┐, Я«цЯ«░Я«хЯ»ЂЯ«фЯ»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕЯ«»Я«┐Я«ЕЯ«ЙЯ«▓Я»Ї Я«хЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«фЯ»ЇЯ«фЯ«цЯ»Ђ ____________.
2. 10 Я«цЯ«░Я«хЯ»ЂЯ«фЯ»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї 265 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я«ЙЯ«ЕЯ«цЯ»Ђ _______________________.
3. Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«цЯ«░Я«хЯ»ЂЯ«фЯ»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«єЯ«ЋЯ«┐Я«»Я«хЯ»ѕ Я««Я»ЂЯ«▒Я»ѕЯ«»Я»Є 407 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 11 Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«цЯ«░Я«хЯ»ЂЯ«фЯ»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕЯ«»Я«ЙЯ«ЕЯ«цЯ»Ђ ___________.