தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் | கணிதம் - நிகழ்தகவு | 10th Mathematics : UNIT 8 : Statistics And Probability
10வது கணக்கு : அலகு 8 : புள்ளியியலும் நிகழ்தகவும்
நிகழ்தகவு
நிகழ்தகவு (Probability)
சில நூற்றாண்டுகளுக்கு முன்பு, சூதாட்டம் மற்றும் கேமிங் போன்றவை நாகரிகமாகக் கருதப்பட்டுப் பல ஆண்டுகள் மக்கள் மத்தியில் பரவலாகப் பிரபலமடைந்தன. அவ்வாறு விளையாடுபவர்கள் குறிப்பிட்ட தருணத்தில் தங்களது வெற்றி தோல்வி வாய்ப்புகளை அறிந்து கொள்ள மிகவும் ஆர்வம் கொண்டதால் இந்த விளையாட்டுகள் மாறத் தொடங்கின 1654ஆம் ஆண்டில் செவாலியர் டீ மெரி என்பார் சூதாட்டத்தில் ஆர்வம் கொண்ட ஒரு பிரெஞ்சு மேலதிகாரி. அக்காலத்தில் மிகவும் முக்கியக் கணிதவியலாளராக திகழ்ந்த பிளெய்ஸ் பாஸ்கல் அவர்களுக்குக் கடிதம் எழுதினார். அதில் சூதாட்டத்தின் மூலம் எவ்வளவு லாபத்தைப் பெற முடியும் என்ற முடிவைத் தெரிவிக்குமாறு குறிப்பிட்டிருந்தார். பாஸ்கல் இந்தப் புதிரைக் கணிதமுறையில் செய்து பார்த்து, அவரது நல்ல நண்பரும் கணிதவியலாளருமான பியரி டி ஃபெர்மா எப்படித் தீர்ப்பார் எனக் கண்டறிய முற்பட்டு அவரிடம் தெரிவித்தார். இவர்கள் இருவரிடையே ஏற்பட்ட கணிதச் சிந்தனைகளே "நிகழ்தகவு" எனும் கணித உட்பிரிவு தோன்ற வழிவகுத்தது.

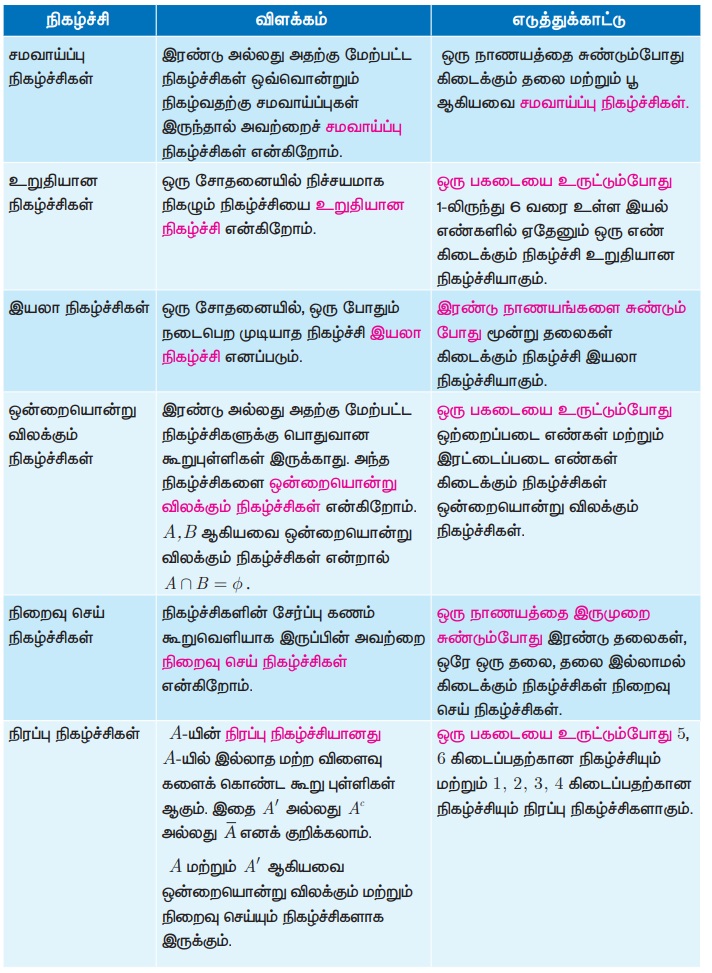
சமவாய்ப்புச் சோதனை
ஒரு சமவாய்ப்புச் சோதனை என்பதில்
(i) மொத்த வாய்ப்புகள் அறியப்படும் (ii) குறிப்பிட்ட வாய்ப்புகள் அறியப்படாது
எடுத்துக்காட்டு :
1. ஒரு நாணயத்தைச் சுண்டுதல்.
2. பகடையை உருட்டுதல்.
3. 52 சீட்டுகள் கொண்ட சீட்டுக் கட்டில் இருந்து ஒரு சீட்டைத் தேர்ந்தெடுத்தல்
கூறுவெளி (Sample space)
ஒரு சமவாய்ப்புச் சோதனையில் கிடைக்கப்பெறும் அனைத்துச் சாத்தியமான விளைவுகளின் தொகுப்பு கூறுவெளி எனப்படுகிறது. இதைப் பொதுவாக S என்று குறிப்பிடலாம்.
எடுத்துக்காட்டு : நாம் ஒரு பகடையை உருட்டும்போது, அனைத்துச் சாத்தியமான விளைவுகள் அதன் முக மதிப்புகளாக 1, 2, 3, 4, 5, 6 எனக் கிடைக்கும். எனவே, கூறுவெளி S = {1,2,3,4,5,6}

கூறு புள்ளி (Sample point)
ஒரு கூறுவெளியிலுள்ள ஒவ்வொரு உறுப்பும் கூறு புள்ளி என்று அழைக்கப்படுகிறது.
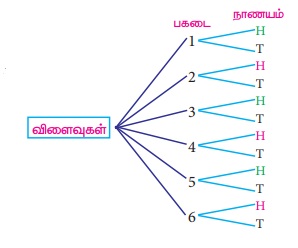
1. மர வரைபடம் (Tree diagram)
ஒரு சமவாய்ப்புச் சோதனையின் அனைத்துச் சாத்தியமான விளைவுகளையும் மர வரைபடம் மூலம் எளிதாக வெளிப்படுத்தலாம். ஒரு மர வரைபடத்தில் உள்ள ஒவ்வொரு கிளையும் சாத்தியமான விளைவைப் பிரதிபலிக்கிறது.
விளக்கம்
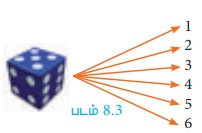
(i) நாம் ஒரு பகடையை உருட்டும் போது, மர வரைபடத்திலிருந்து
கூறுவெளியை, S = {1,2,3,4,5,6} (படம்.8.3) என எழுதலாம்.
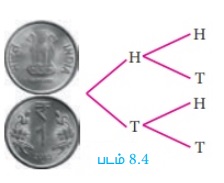
(ii) நாம் இரண்டு நாணயங்களைச் சுண்டும்போது, மர வரைபடத்திலிருந்து கூறுவெளியை S = {HH, HT, TH, TT} என எழுதலாம். (படம்.8.4)
எடுத்துக்காட்டு 8.17
மர வரைபடத்தைப் பயன்படுத்தி இரண்டு பகடைகள் உருட்டப்படும்போது கிடைக்கும் கூறுவெளியை எழுதுக.
தீர்வு
இரண்டு பகடைகள் உருட்டப்படும்போது, ஒவ்வொரு பகடையிலும் 6 முக மதிப்புகள் 1, 2, 3, 4, 5, 6 என உள்ளதால் கீழ்க்காணும் மர வரைபடத்தைப் பெறலாம்
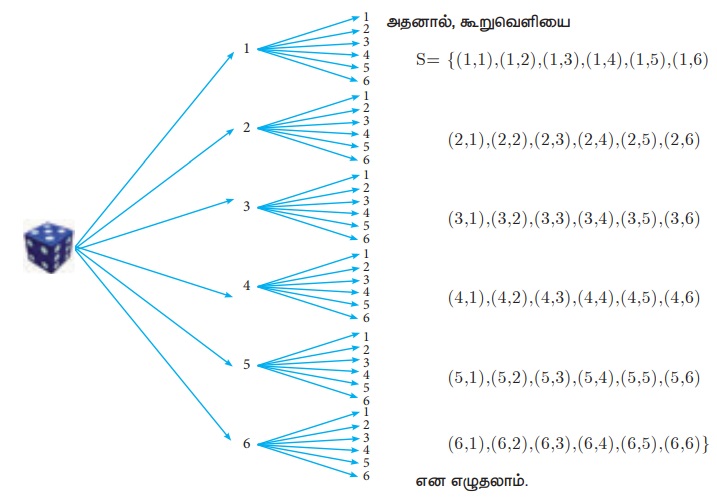
அதனால், கூறுவெளியை
S= {(1,1),(1,2),(1,3),(1,4),(1,5),(1,6)
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}
என எழுதலாம்.
முன்னேற்றச் சோதனை
1. ஒரு குறிப்பிட்ட விளைவைக் கணிக்க முடியாமல் இருக்கும் ஒரு சோதனையை ______ என்போம்.
2. அனைத்துச் சாத்தியமானக் கூறுகளின் தொகுப்பையும் ______ என அழைக்கிறோம்.
நிகழ்ச்சி : ஒரு சமவாய்ப்புச் சோதனையில் கிடைக்கும் ஒவ்வொரு விளைவும் நிகழ்ச்சி என்கிறோம். எனவே, ஒரு நிகழ்ச்சி கூறுவெளியின் உட்கணமாக இருக்கும்.
எடுத்துக்காட்டு : இரண்டு நாணயங்களை சுண்டும் பொழுது, இரண்டும் தலைகளாக கிடைக்கப் பெறுவது ஒரு நிகழ்ச்சி.
முயற்சி : ஒரு சோதனையை ஒரு முறை செய்வது முயற்சியாகும். எடுத்துக்காட்டு : ஒரு நாணயத்தை மூன்றுமுறை சுண்டும்பொழுது, ஒவ்வொருமுறை சுண்டுதலும் ஒரு முயற்சியாகும்.
குறிப்பு
ஒரே ஒரு விளைவு நிகழ்ச்சி: E என்ற நிகழ்ச்சியில் ஒரேயொரு விளைவு மட்டும் இருந்தால் அதற்கு ஒரேயொரு விளைவு நிகழ்ச்சி என்று பெயர்
உங்களுக்குத் தெரியுமா?
1713-ல் பெர்னோலி முதன்முதலில் நிகழ்தகவைச் சூதாட்டத்தைத் தவிரப் பல இடங்களில் மிகப்பெரிய அளவில் பயன்படுத்திக்காட்டினார்
2. ஒரு நிகழ்ச்சியின் நிகழ்தகவு (Probability of an Event)
ஒரு சம வாய்ப்பு சோதனையில், S என்பது கூறுவெளி மற்றும் E ⊆ S. இங்கு, E ஆனது ஒரு நிகழ்ச்சி. E என்ற நிகழ்ச்சி நிகழ்வதற்கான நிகழ்தகவானது,

நிகழ்தகவின் இந்த வரையறையானது முடிவுறு கூறுவெளிகளுக்கு மட்டுமே பொருந்தும். எனவே இந்தப் பாடப்பகுதியில் முடிவுறு கூறுவெளியை உடைய கணக்குகளையே கருத்தில் கொள்கிறோம்.

முன்னேற்றச் சோதனை
கொடுக்கப்பட்ட எண்களில் எவை நிகழ்தகவாக இருக்க முடியாது?
(a) -0.0001
(b) 0.5
(c) 1.001
(d) 1
(e) 20%
(f) 0.253
(g) 1-√5/2
(h) √3 + 1 / 4
எடுத்துக்காட்டு 8.18
ஒரு பையில் 5 நீல நிறப்பந்துகளும், 4 பச்சை நிறப்பந்துகளும் உள்ளன. பையிலிருந்து சமவாய்ப்பு முறையில் ஒரு பந்து எடுக்கப்படுகிறது. எடுக்கப்படும் பந்தானது (i) நீலமாக (ii) நீலமாக இல்லாமல் இருப்பதற்கான நிகழ்தகவைக் காண்க.
தீர்வு
மொத்த வாய்ப்புகளின் எண்ணிக்கை n(S) = 5 + 4 = 9
(i) A என்பது நீல நிறப்பந்தை பெறுவதற்கான நிகழ்ச்சி என்க.
A நிகழ்வதற்கான வாய்ப்புகளின் எண்ணிக்கை, n(A) = 5
நீலநிறப் பந்து கிடைப்பதற்கான நிகழ்தகவு, P (A) = n(A)/ n(S) = 5/9
(ii) ![]() ஆனது நீல நிறப்பந்து கிடைக்காமல் இருக்கும் நிகழ்ச்சி. எனவே, P (
ஆனது நீல நிறப்பந்து கிடைக்காமல் இருக்கும் நிகழ்ச்சி. எனவே, P (![]() ) = 1 − P (A) = 1 – 5/9 = 4/9
) = 1 − P (A) = 1 – 5/9 = 4/9
எடுத்துக்காட்டு 8.19
இரண்டு பகடைகள் உருட்டப்படுகின்றன. கிடைக்கப்பெறும் முக மதிப்புகளின் கூடுதல் (i) 4 - க்குச் சமமாக (ii) 10 -ஐ விடப் பெரிதாக (iii) 13 -ஐ விடக் குறைவாக இருப்பதற்கான நிகழ்தகவு காண்க.
தீர்வு
இரண்டு பகடைகள் உருட்டப்படும்பொழுது, கூறுவெளியானது
S = { (1,1),(1,2),(1,3),(1,4),(1,5),(1,6)
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6) }; எனவே, n (S) = 36
(i) A ஆனது முக மதிப்புகளின் கூடுதல் 4-ஆக இருப்பதற்கான நிகழ்ச்சி என்க.
A = {(1,3),(2,2),(3,1)}; n (A) = 3
முகமதிப்புகளின் கூடுதல் 4 கிடைப்பதற்கான நிகழ்தகவானது P (A) = n(A)/n(S) = 3/36 =1/12
(ii) B ஆனது முக மதிப்புகளின் கூடுதல் 10-ஐ விட பெரிய எண்ணாக இருப்பதற்கான நிகழ்ச்சி என்க.
B = {(5,6),(6,5),(6,6)}; n (B) = 3
கூடுதல் 10 ஐ விட பெரிதாக கிடைப்பதற்கான நிகழ்தகவானது P (B) = n(B)/n(S) = 3/36 =1/12
(iii) C ஆனது முக மதிப்புகளின் கூடுதல் 13-ஐ விட குறைவாக இருப்பதற்கான நிகழ்ச்சி என்க. எனவே C = S.
ஆகவே, n (C) = n (S) = 36
ஆகையால், முக மதிப்புகளின் கூடுதல் 13 -ஐ விடக் குறைவானதாக இருப்பதற்கான நிகழ்தகவு P (C) = n(C)/n(S) = 36/36 = 1
எடுத்துக்காட்டு 8.20
இரண்டு நாணயங்கள் ஒன்றாகச் சுண்டப்படுகின்றன. இரண்டு நாணயங்களிலும் வெவ்வேறு முகங்கள் கிடைப்பதற்கான நிகழ்தகவு என்ன?
தீர்வு
இரண்டு நாணயங்கள் சுண்டப்படும்பொழுது அதன் கூறுவெளியானது
S = {HH, HT, TH, TT } ; n(S) = 4
A ஆனது நாணயங்களில் வெவ்வேறு முகங்கள் கொண்ட நிகழ்ச்சி என்க.
A = {HT, TH}; n(A) = 2
நாணயங்களில் வெவ்வேறு முகங்கள் கிடைப்பதற்கான நிகழ்தகவானது
P(A) =n(A)/n(S) = 2/4 = 1/2
எடுத்துக்காட்டு 8.21
நன்கு கலைத்து அடுக்கப்பட்ட 52 சீட்டுளைக் கொண்ட சீட்டுக்கட்டிலிருந்து, சமவாய்ப்பு முறையில் ஒரு சீட்டு எடுக்கப்படுகிறது. அது
(i) சிவப்பு நிறச் சீட்டு
(ii) ஹார்ட் சீட்டு
(iii) சிவப்பு நிற இராசா
(iv) முக சீட்டு
(v) எண் சீட்டாக இருப்பதற்கான நிகழ்தகவைக் கண்டறிக.
தீர்வு
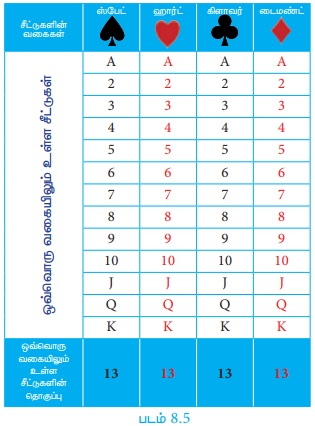
n (S) = 52
(i) A என்பது சிவப்புச் சீட்டு கிடைக்கும் நிகழ்ச்சி என்க.
n (A) = 26
சிவப்பு சீட்டுகள் கிடைப்பதற்கான நிகழ்தகவு
P (A) = 26/52 = 1/2
(ii) B என்பது ஹார்ட் சீட்டு கிடைக்கும் நிகழ்ச்சி என்க.
n (B) = 13
ஹார்ட் சீட்டுகள் கிடைப்பதற்கான நிகழ்தகவு
P(B) = n(B)/n(S) = 13/52 = 1/4
(iii) C என்பது சிவப்பு நிற இராசா சீட்டு கிடைக்கும் நிகழ்ச்சி என்க.
n (C) = 2
எனவே, சிவப்பு நிற இராசா சீட்டு கிடைப்பதற்கான நிகழ்தகவு
P(C) = n(C)/n(S) = 2/52 = 1/26
(iv) D என்பது முகச்சீட்டு கிடைக்கும் நிகழ்ச்சி என்க. முகச்சீட்டுகளாவன மந்திரி (J), அரசி (Q) மற்றும் இராசா (K).
n(D) = 4 ×3 = 12
முகச்சீட்டுகள் கிடைப்பதற்கான நிகழ்தகவு
P (D) = n(D)/n(S) = 12/52 = 3/13
(v) E என்பது எண் சீட்டு கிடைக்கும் நிகழ்ச்சி என்க. எண் சீட்டுகளாவன 2, 3, 4, 5, 6, 7, 8, 9 மற்றும் 10.
n (E) = 4 ×9 = 36
எண் சீட்டுகள் கிடைப்பதற்கான நிகழ்தகவு
P (E) = n(E)/n(S) = 36/52 = 9/13
எடுத்துக்காட்டு 8.22
ஒரு நெட்டாண்டில் (leap year) 53 சனிக்கிழமைகள் கிடைப்பதற்கான நிகழ்தகவு என்ன?
தீர்வு
ஒரு நெட்டாண்டில் 366 நாட்கள் உள்ளன. எனவே 52 முழு வாரங்களும் மற்றும் 2 நாட்களும் உள்ளன.
52 வாரங்களில், 52 சனிக்கிழமைகள் கிடைத்து விடும். மீதமுள்ள இரண்டு நாட்களுக்கான வாய்ப்புகள் கீழ்க்காணும் கூறுவெளியில் கிடைக்கும்.
S = {ஞாயிறு-திங்கள், திங்கள்-செவ்வாய், செவ்வாய்-புதன், புதன்-வியாழன், வியாழன் - வெள்ளி, வெள்ளி - சனி, சனி - ஞாயிறு}.
n (S) = 7
A என்பது 53-வது சனிக்கிழமை கிடைக்கும் நிகழ்ச்சி என்க.
எனவே A = {வெள்ளி -சனி, சனி-ஞாயிறு}; n (A) = 2
53 சனிக்கிழமைகள் கிடைப்பதற்கான நிகழ்தகவானது P(A) = n (A)/ n (S) = 2/7
சிந்தனைக் களம்
சாதாரண ஆண்டில், 53 சனிக்கிழமைகள் வருவதற்கான நிகழ்தகவு என்ன?
எடுத்துக்காட்டு 8.23
ஒரு பகடை உருட்டப்படும் அதே நேரத்தில் ஒரு நாணயமும் சுண்டப்படுகிறது. பகடையில் ஒற்றைப்படை எண் கிடைப்பதற்கும், நாணயத்தில் தலைக் கிடைப்பதற்குமான நிகழ்தகவைக் காண்க.
தீர்வு
கூறுவெளி, S = {1H,1T,2H,2T,3H,3T,4H,4T,5H,5T,6H,6T};
n(S) = 12
A ஆனது ஒற்றைப்படை எண் மற்றும் தலைக் கிடைப்பதற்கான நிகழ்ச்சி என்க.
A = {1H, 3H, 5H}; n(A) = 3
P (A) = n (A)/ n(S) = 3/12 = 1/4
செயல்பாடு 3
மதுவின் வீட்டிலிருந்து அவள் பணியாற்றும் இடத்திற்கு செல்ல மூன்று வழிகள் R1, R2, மற்றும் R3 உள்ளன. அவளுடைய அலுவலகத்தில் P1, P2, P3, P4 என்ற நான்கு வாகன நிறுத்துமிடங்களும், B1, B2, B3 என்ற மூன்று நுழைவாயில்களும் உள்ளன. அங்கிருந்து அவள் பணிபுரியும் தளத்திற்குச் செல்ல E1, E2 என்ற இரண்டு மின் தூக்கிகள் உள்ளன. மர வரைபடத்தைப் பயன்படுத்தி அவளுடைய வீட்டிலிருந்து அலுவலகத் தளத்தை அடைய எத்தனை வழிகள் உள்ளன எனக் காண்க?
செயல்பாடு 4
தேவையான தகவல்களைச் சேகரித்துக் கீழ்க்கண்டவற்றின் நிகழ்தகவுகளைக் காண்க.
(i) உன்னுடைய வகுப்பிலுள்ள ஒரு மாணவனைத் தேர்ந்தெடுக்க.
(ii) உன்னுடைய வகுப்பிலுள்ள ஒரு மாணவியைத் தேர்ந்தெடுக்க.
(iii) உனது பள்ளியில் பத்தாம் வகுப்பு பயில்பவர்களில் ஒருவரைத் தேர்வு செய்ய.
(iv) உனது பள்ளியில் பத்தாம் வகுப்பில் பயிலும் ஒரு மாணவனைத் தேர்வு செய்ய
(v) உனது பள்ளியில் பத்தாம் வகுப்பில் பயிலும் ஒரு மாணவியைத் தேர்வு செய்ய.
எடுத்துக்காட்டு 8.24
ஒரு பையில் 6 பச்சை நிறப்பந்துக்களும், சில கருப்பு மற்றும் சிவப்பு நிறப்பந்துகளும் உள்ளன. கருப்பு பந்துகளின் எண்ணிக்கை, சிவப்பு பந்துகளைப் போல் இருமடங்காகும். பச்சை பந்து கிடைப்பதற்கான நிகழ்தகவு சிவப்பு பந்து கிடைப்பதற்கான நிகழ்தகவைப் போல் மூன்று மடங்காகும். இவ்வாறெனில், (i) கருப்பு பந்துகளின் எண்ணிக்கை (ii) மொத்தப் பந்துகளின் எண்ணிக்கை ஆகியவற்றைக் காண்க
தீர்வு
பச்சை பந்துகளின் எண்ணிக்கை n(G) = 6
சிவப்பு பந்துகளின் எண்ணிக்கை n(R) = x என்க
எனவே, கருப்பு பந்துகளின் எண்ணிக்கை n(B) = 2x
மொத்தப் பந்துகளின் எண்ணிக்கை n(S) = 6 + x + 2x = 6 + 3x
கொடுக்கப்பட்டது, P (G) = 3 × P(R)
6/ (6+3x) = 3 × x/(6 + 3x)
3x = 6 லிருந்து, x = 2
(i) கருப்பு பந்துகளின் எண்ணிக்கை = 2 × 2 = 4
(ii) மொத்தப் பந்துகளின் எண்ணிக்கை = 6 + (3 × 2) = 12
எடுத்துக்காட்டு 8.25
படத்தில் காட்டியுள்ள அம்புக்குறி சுழற்றும் விளையாட்டில் 1, 2, 3, ... 12 என்ற எண்கள் சமவாய்ப்பு முறையில் கிடைக்க வாய்ப்புள்ளது. அம்புக்குறியானது (i) 7 (ii) பகா எண் (iii) பகு எண் ஆகியவற்றில் நிற்பதற்கான நிகழ்தகவுகளைக் கண்டறிக.
தீர்வு
கூறுவெளி S = {1,2,3,4,5,6,7,8,9,10,11,12}; n(S) = 12
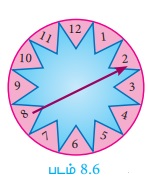
(i) A ஆனது, அம்புக்குறி எண் 7-ல் நிற்பதற்கான நிகழ்ச்சி என்க.
n(A) = 1
P (A) = n(A)/n(S) = 1/12
(ii) B ஆனது அம்புக்குறி பகா எண்ணில் நிற்பதற்கான நிகழ்ச்சி என்க.
B = {2,3,5,7,11}; n (B) = 5
P (B) = n(B)/n(S) = 5/12
(iii) C ஆனது அம்புக்குறி பகு எண்ணில் நிற்பதற்கான நிகழ்ச்சி என்க.
C = {4,6,8,9,10,12}; n (C) = 6
P (C) = n(C)/n(S) = 6/12 = 1/2
சிந்தனைக் களம்
இயலா நிகழ்ச்சியின் நிரப்பு நிகழ்ச்சி எது?