சுழல் இயக்கவியல்

சுழல் இயக்கவியல் (ROTATIONAL DYNAMICS)

திருப்பு விசை, கோண முடுக்கம், கோண உந்தம், கோணத் திசைவேகம் மற்றும் நிலைத்திருப்புத் திறன் இவைகளுக்கு இடையேயான தொடர்புகளைப் பகுதி 5.2 இல் பயின்றோம். இதன் தொடர்ச்சியாக இப்பகுதியில் திண்மப்பொருள் ஒன்றின் மீது திருப்பு விசையினால் செய்யப்பட்ட வேலை, இயக்க ஆற்றல் போன்ற இயக்கவியல் அளவுகளுக்கு இடையேயான தொடர்புகளைப் பயிலலாம். இறுதியாக இடப்பெயர்வு இயக்கத்திற்கும், சுழற்சி இயக்கத்திற்கும் தொடர்புடைய அளவீடுகளை ஒப்பிடலாம்.

திண்மப் பொருட்களின் மீது திருப்பு விசையின் விளைவு 

திண்மப் பொருள் ஒன்றின் மீது சுழலும் அச்சைப் பொருத்து புற திருப்பு விசை செயல்படும்போது சுழலும் பொருளானது அச்சைப் பொறுத்து கோண முடுக்கத்தைப் பெறுகிறது. திருப்பு விசைக்கும் கோண முடுக்கத்திற்கும் இடையேயான தொடர்பு எண்மதிப்பில்

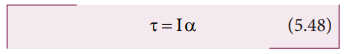
இங்கு, I என்பது திண்மப்பொருளின் நிலைமத்திருப்புத்திறன் ஆகும். சுழற்சி இயக்கத்தில் திருப்பு விசை என்பது நேர்கோட்டு இயக்கத்தில் விசைக்குச் சமானமானது.

கோணஉந்த மாறா விதி

வெளிப்புற திருப்புவிசை செயல்படாத வரை, சுழலும் திண்மப் பொருளின் மொத்தக் கோண உந்தம் மாறாது. இதுவே கோண உந்த மாறா விதி

கோண உந்தம் L = Iω, எனும் போது 

கோண உந்த மாறா விதியின்படி 

தொடக்க கோண உந்தம் = இறுதி கோண உந்தம்.

இச்சமன்பாட்டின் மூலம், கோண உந்தம் மாறாமல் இருக்க I அதிகரிக்கும் போதும் ω குறையவும், அல்லது ω அதிகரிக்கும் போது I குறையவும் செய்யும் என அறியலாம். 

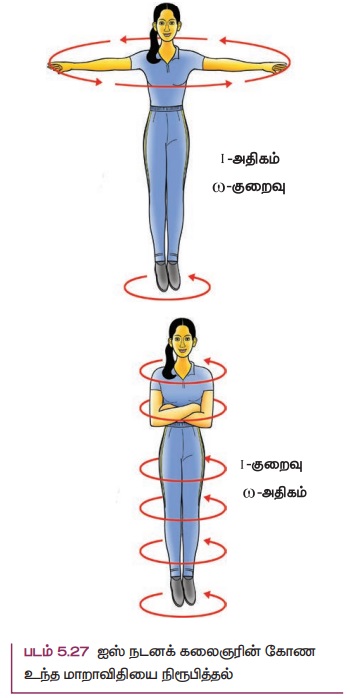
கோண உந்த மாறா விதியின் தத்துவமானது பல சூழ்நிலைகளில் பயன்பாட்டில் உள்ளது. மிகச் சிறந்த உதாரணமான ஐஸ் நடனக் கலைஞரின் சுழற்சி விளையாட்டு படம் 5.27 இல் காட்டப்பட்டுள்ளது. நடனக் கலைஞர் தன்னைத் தானே சுழற்றும் போது அவரது கைகளை வெளிப்புறமாக நீட்டினால் சுழலும் வேகம் குறைகிறது. ஏனென்றால் கைகளை உடலுக்கு வெளிப்புறமாக நீட்டும் போது நிலைமத்திருப்புத்திறன் அதிகரிப்பதால் கோணத்திசைவேகம் குறைந்து சுழலும் வேகம் குறைகிறது. கைகளை உடலை நோக்கி உட்புறமாக மடக்கும் போது நிலைமத்திருப்புத்திறன் குறைவதால் சுழலும் வேகம் அதிகரிக்கிறது.

திருப்பு விசையினால் செய்யப்பட்ட வேலை

திண்மப்பொருளொன்று நிலையான அச்சைப் பற்றி சுழல்கிறது எனக் கொள்க. இந்தப்பாடப் புத்தகத் தாளின் தளத்திற்குச் செங்குத்தான அச்சைப் பொறுத்துச் சுழலக் கூடிய பொருள் ஒன்றின் குறுக்கு வெட்டுத் தோற்றத்தைப் படம் 5.29 இல் காணலாம். F என்ற தொடுகோட்டு விசை பொருளின் மீது P என்ற புள்ளியில் செயல்படுகிறது.

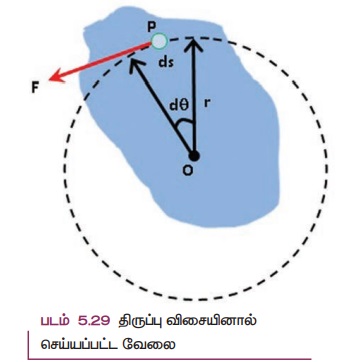
இந்தத் தொடுகோட்டு விசை F ஆனது பொருளைச் சிறிய அளவில் இடப்பெயர்ச்சி (ds) செய்கிறது. விசையினால் செய்யப்பட்ட வேலை (dW)

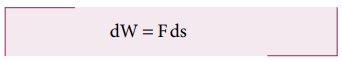
இடப்பெயர்ச்சி ds க்கும் சுழற்சிக் கோணம் dθ க்கும் இடையேயான தொடர்பு

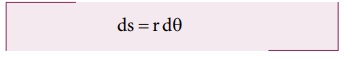
விசையினால் செய்யப்பட்ட வேலைக்கான சமன்பாடு

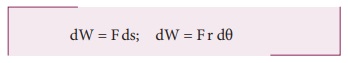
இதில் F r ஆனது விசையினால் பொருளின் மீது உருவாக்கப்பட்ட திருப்பு விசை τ என்பதால்,

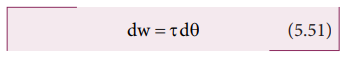
ஒரு நிலையான அச்சைப் பொருத்து சுழலும் பொருளின் மீது வெளிப்புறத் திருப்பு விசையினால் (τ) செய்யப்பட்ட வேலை மேற்கண்ட சமன்பாட்டினால் பெறப்படுகிறது. 

இடப்பெயர்வு இயக்கத்திற்குத் தொடர்புடைய விசையினால் செய்யப்பட்ட வேலையின் சமன்பாடு.

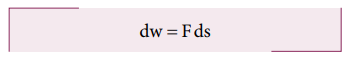
சுழற்சி இயக்கத்தின் இயக்க ஆற்றல் 

திண்மப் பொருள் ஒன்று அச்சைப் பொருத்துக் கோணத் திசைவேகம் ω வுடன் சுழல்வதைப் படம் 5.30 இல் காணலாம். பொருளில் உள்ள ஒவ்வொரு துகளும் அச்சைப் பொறுத்து ஒரே கோண திசைவேகத்தையும் (ω) ஆனால் வெவ்வேறான தொடுகோட்டுத் திசைவேகங்களையும், பெற்றிருக்கும். 

சுழலும் அச்சிலிருந்து mi, நிறையுடன் ri தொலைவில் உள்ள துகளைக் கருதுக. இந்தத் துகள் கீழ்க்கண்ட சமன்பாட்டின் vi = ri ω தொடுகோட்டுத் திசைவேகம் கொண்டிருந்தால் அத்துகளின் இயக்க ஆற்றல்,

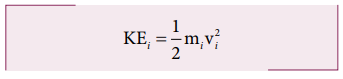
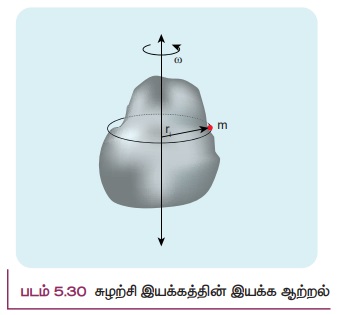
இச்சமன்பாட்டை கோண திசைவேகத்தைப் பயன்படுத்தி எழுத

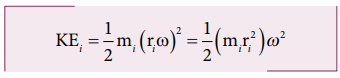
இதே போன்ற துகள்களால் ஆக்கப்பட்டுள்ள மொத்த பொருளின் இயக்க ஆற்றல்

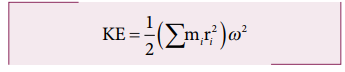
இங்கு Σmi ri2, என்பது பொருளின் நிலைமத்திருப்புத்திறனாகும்

I = Σmi ri2

திண்மப் பொருளின் சுழற்சி இயக்கத்தில் இயக்க ஆற்றலுக்கான சமன்பாடு

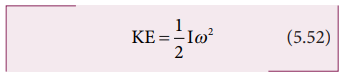
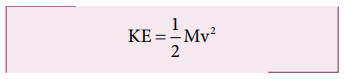
சுழல் இயக்க ஆற்றலுக்கும் கோண உந்தத்திற்கும் இடையேயான தொடர்பு 

நிலைமத் திருப்புத்திறன் I கொண்ட திண்மப்பொருளொன்று ω கோணத்திசை வேகத்துடன் சுழல்கிறது எனக் கொள்க.

பொருளின் கோண உந்தம், L = I ω 

பொருளின் சுழல் இயக்க ஆற்றல், KE = 1/2 Iω2

இச்சமன்பாட்டின் பகுதியையும் தொகுதியையும் I ஆல் பெருக்க, I மற்றும் இயக்க ஆற்றல் (KE) இடையேயான தொடர்பைப் பெறலாம்,

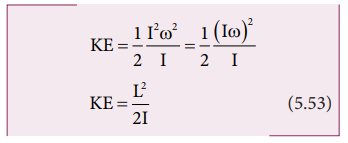
திருப்பு விசையின் திறன் (Power Delivered by Torque)

திறன் என்பது ஓரலகு நேரத்தில் செய்யப்பட்ட வேலையாகும். செய்யப்பட்ட வேலையை வேலை செய்யப்பட்ட சிறிய நேரத்தால் வகுக்க கிடைப்பது. உடனடித்திறன் (P) எனப்படும்.

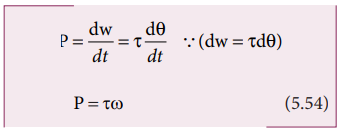
இந்தச் சமன்பாட்டிற்கு இணையான இடப்பெயர்ச்சி இயக்கத்தின் உடனடித் திறனிற்கான சமன்பாடு

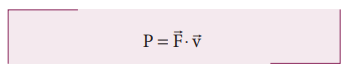
இடப்பெயர்ச்சி மற்றும் சுழற்சி இயக்க அளவுகளுக்கான ஒப்பீடு

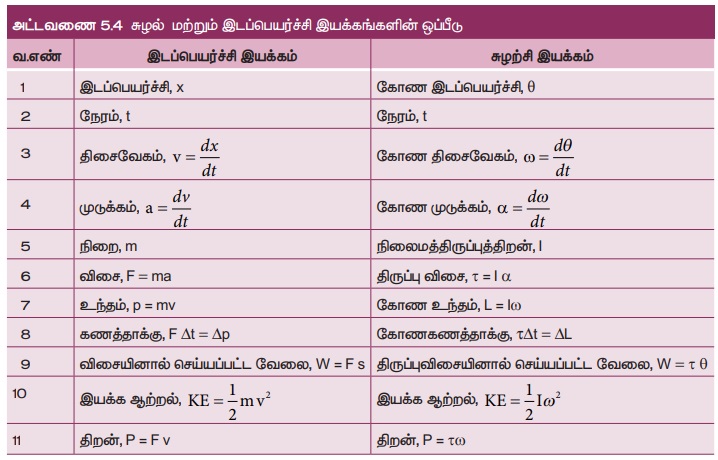
சுழற்சி இயக்கத்திலுள்ள பெரும்பான்மையான சமன்பாடுகள் இடப்பெயர்ச்சி இயக்கத்தினைப்போன்றே இருப்பதால் சுழற்சி இயக்கத்தில் உள்ள அளவுகளை இடப்பெயர்ச்சி இயக்கத்தில் உள்ள அளவுகளோடு அட்டவணை 5.4 இல் ஒப்பிடப்பட்டுள்ளது.

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் திண்மப் பொருட்களின் மீது திருப்பு விசையின் விளைவு

எடுத்துக்காட்டு 5.18

500g நிறையும் 10cm ஆரமும் கொண்ட வட்டத்தட்டு ஒன்று தன்னிச்சையாக படத்தில் காட்டப்பட்டது போல நிலையான அச்சைப் பொருத்துச் சுழல்கிறது. எடையற்ற மற்றும் மீட்சித்தன்மையற்ற கம்பியானது வட்டத்தின் விளம்பில் சுற்றுகள் சுற்றப்பட்டு மற்றொரு முணையானது 100g நிறையுடன் இணைக்கப்பட்டுள்ளது. 100g நிறையின் முடுக்கத்தை காண்க. (தகவல்: கம்பியானது வட்டத்தட்டின் விளிம்பில் நழுவவில்லை. மாறாக வட்டத்தட்டுடன் சுழல்கிறது g = 10 ms-2]

தீர்வு

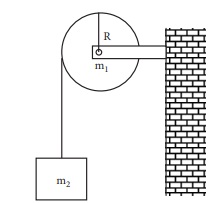
வட்டத்தட்டின் நிறையை m1 எனவும் அதன் ஆரத்தை R எனவும் கொள்க. தொங்கவிடப்பட்ட பொருளின் நிறை m2.

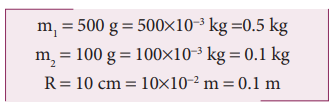
வட்டத்தட்டின் விளம்பில் பல முறை சுற்றப்பட்டுள்ள மிகக் குறைந்த நிறையுள்ள மற்றும் மீட்சியற்ற கம்பியானது நழுவுதல் இல்லாமல் வட்டத் தட்டுடன் சுழல்கிறது. நிறை m2 வின் தொடுகோட்டு முடுக்கமும் நிறை m1 இன் இடம்பெயர்வு முடுக்கமும் சமம் m1 மற்றும் m2 விற்கு தனித்தனியே தனித்த பொருளின் விசை (FBD) (Free Body Diagram) படத்தை வரைக.

வட்டத்தட்டிற்கான தனித்த பொருளின் விசைப்படம் (FBD) (Free Body Diagram)

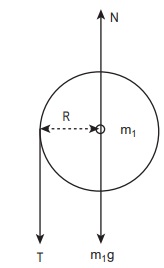
வட்டத்தட்டின் மீது செயல்படும் புவியீர்ப்பு விசை (m1g) ஆனது கீழ்நோக்கியும் வட்டத்தட்டானது மையத்தில் பொருத்தப்பட்டுள்ள மையப் புள்ளியின் வழியாக செங்குத்து விசை (N) யும் செயல்படுகிறது. வட்டத்தட்டின் பரிதியில் சுழலும் அச்சிற்குச் செங்குத்தாகக் கீழ்நோக்கி இழுவிசை T செயல்படுகிறது. மேலும் புவியீர்ப்பு விசையும் (m1g) யும் செங்குத்து விசைNம் ஒன்றை ஒன்று சமன்செய்கிறது. m1g = N 

இழுவிசை T ஆனது திருப்பு விசையை (R T) அளிப்பதால் வட்டத்தட்டானது கோண முடுக்கம் 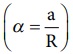வுடன் சுழற்சி இயக்கத்திற்கு உட்படுகிறது. இங்கு a என்பது வட்டத்தட்டின் விட்டத்தில் உள்ள புள்ளி தொடுவியல் திசையில் உணரும் நேர்கோட்டு முடுக்கமாகும். இவ்வட்டத்தட்டின் நிலைத்திருப்புத்திறன் I மற்றும் இதன் சுழற்சி ஆரம் K எனில்

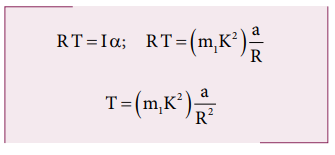
கம்பியின் ஒரு முனையில் கட்டப்பட்ட நிறையின் தனித்த பொருளின் விசைப்படம் (FBD) 

இதன் புவியீர்ப்பு விசை (m2g) கீழ்நோக்கிச் செயல்படுகிறது மற்றும் இழுவிசை T மேல்நோக்கி செயல்படுகிறது. இவற்றின் தொகு பயன் விசை நிறையின் மீது கீழ்நோக்கிச் செயல்படுகிறது. (T < m2g)

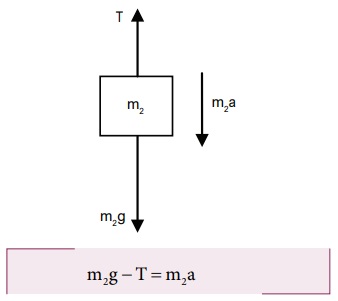
வட்டத்தட்டினால் செயல்படும் இழுவிசை T யை பிரதியிட

என்ற சமன்பாடு வட்டத்தட்டின் தளத்திற்கு செங்குத்தாகவும் மையம் வழிச் செல்லும் அச்சைப் பற்றி சுழல்வதால் பிரதியிட்டு சுருக்க, 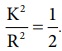முடுக்கத்திற்கான சமன்பாடு கீழ்க்கண்டவாறு கிடைக்கும்.

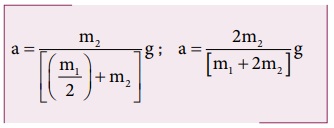
மதிப்புகளைப் பிரதியிட,

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் கோணஉந்த மாறா விதி

எடுத்துக்காட்டு 5.19

ω கோணத் திசைவேகத்துடன் சுழலும் வட்ட மேசையின் மீது சர்க்கஸ் வீரர் ஒருவர் கைகளை நீட்டிய நிலையில் உள்ளார். அவர் கைகளைத் தன்னை நோக்கி உட்புறமாக மடக்கும் போது நிலைமத்திருப்புத் திறனானது ஆரம்ப மதிப்பிலிருந்து மூன்றில் ஒரு பங்காகக் குறைகிறது. அவரது புதிய நிலையில் கோண திசை வேகத்தை காண்க. (தகவல் - புறத்திருப்பு விசை செயல்படாத நிலையில்) 

தீர்வு 

கைகள் நீட்டப்பட்ட நிலையில் சர்க்கஸ் வீரரின் நிலைமத்திருப்புத்திறன் I என்க. சர்க்கஸ் வீரரின் மீதும் சுழல்மேசை மீதும் திருப்பு விசை எதுவும் செயல்படாத நிலையில் கோண உந்தம் மாறாது எனவே கோண உந்தத்தின் சமன்பாடானது.

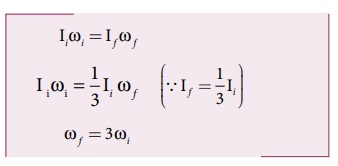
மேற்கண்ட முடிவிலிருந்து ஆரம்பக் கோணத் திசைவேகமானது மூன்று மடங்கு அதிகரித்துள்ளது என்பது தெளிவாகிறது.

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் சுழற்சி இயக்கத்தின் இயக்க ஆற்றல்

எடுத்துக்காட்டு 5.20

9 kg நிறையும் 3 m ஆரமும் கொண்ட வளையமானது, அந்த வளையத்தின் தளத்திற்கு செங்குத்தாகவும், மையம் வழிச் செல்லும் அச்சைக் பற்றி 240 rpm வேகத்தில் சுழலும்போது அது பெற்றுள்ள சுழல் இயக்க ஆற்றலை கணக்கிடுக. 

தீர்வு 

பொருளின் சுழல் இயக்க ஆற்றல்,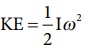

வளையத்தின் நிலைமத்திருப்புத்திறன் I = MR2