தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள்: இயற்பியல் : துகள்களாலான அமைப்பு மற்றும் திண்மப்பொருட்களின் இயக்கம்

பயிற்சி கணக்குகள்

1. 100g நிறையுள்ள சீரான வட்டத்தட்டின் விட்டம் 10cm கிடைத்தள மேசையின் மீது 20cms-1 திசைவேகத்துடன் உருளும்போது அதன் மொத்த ஆற்றலை கணக்கிடுக. 

m = 100g = 100 × 10-3 Kg 

D = 10 cm = 10 × 10-2 m 

V = 20 cms-1 = 20 × 10-2 ms-1 

R = 5 × 10-2 m

தீர்வு :

2. 5 அலகுகள் நிறை கொண்ட ஒரு துகள் v = 3 √ 2 அலகுகள் சீரான வேகத்துடன் XOY தளத்தில் y = x + 4 என்ற சமன்பாட்டின் படி இயங்குகிறது. அத்துகளின் கோண உந்தத்தை காண்க.

m = 5 

v = 3 √ 2 

y = x + 4 

L = ? 

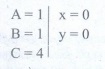
Ax + By + C = 0 மையத்திலிருந்து செங்குத்து தொலைவிற்கான சமன்பாடு

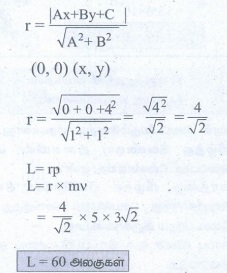
விடை: 60 அலகுகள் 

3. சுழலும் சக்கரமொன்று சீரான கோண முடுக்கத்துடன் சுழல்கிறது. இதன் கோணத் திசைவேகம் 20𝜋rads-1 லிருந்து 40𝜋rads-1 க்கு 10 வினாடிகளில் அதிகரிக்கப்படுகிறது எனில் சுற்றுகளின் எண்ணிக்கையை காண்க.

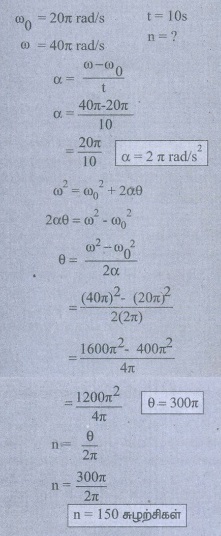
விடை: 150 சுழற்சிகள்

4. m நிறையும் l நீளமும் கொண்ட தண்டு அதன் ஒரு முனையின் வழிச் செல்லும் அச்சைப் பொருத்து θ கோணத்தை ஏற்படுத்துகிறது. அந்த அச்சைப் பற்றிய நிலைமத் திருப்புத்திறனைக் காண்க. 

தீர்வு:

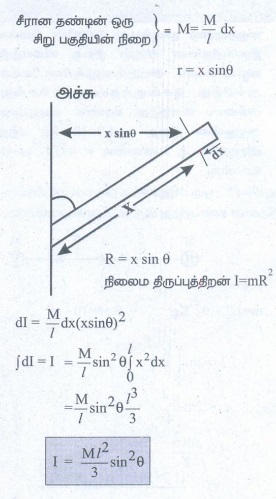
விடை: 1/12  Ml 2 sin2 θ

5. இரு துகள்கள் P மற்றும் Q என்பனவற்றின் நிறைகள் முறையே 1Kg மற்றும் 3Kg அவற்றிற்கு இடையேயான கவர்ச்சி விசையினால் 30ms-1 மற்றும் 6ms-1 என்ற திசைவேகங்களுடன் ஒன்றை ஒன்று நோக்கி நகர்கின்றன. அவற்றின் நிறை மையங்களின் திசைவேகங்கள் என்ன? 

தீர்வு: 

m1 = 1 Kg v1 = 30ms-1 

m2 = 3 Kg v2 = -6ms-1

vcm = m1v1 + m2 v2 / m1m2

இரு துகள்களும் ஒன்றை ஒன்று நோக்கி நகர்வதால்

Vcm = 0

விடை: ௦

6. ஹைட்ரஜன் மூலக்கூறு ஒன்றின் நிலைமத் திருப்புதிறனை அதன் நிறை மையத்தின் வழியாகவும், அணுக்களுக்கிடையேயான அச்சிற்கு செங்குத்தாகவும் செல்லும் அச்சைப் பொருத்து காண்க. ஹைட்ரஜன் அணுவின் நிறை = 1.7 × 10-27Kg மற்றும் அணுவிடைத் தொலைவு = 4 × 10-10 m என கொள்க. 

குறிப்பு : ஒரு அணுவிற்கு நிலைமைத் திருப்புத் திறனை கண்டறிந்து இரு மடங்காக கணக்கிடுக.

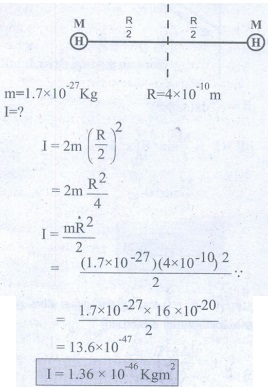
விடை: 1.36 × 10-46 kg m2

கருத்துரு வினாக்கள்

1. மரம் வெட்டப்படும்போது, மரமானது வெட்டி வீழ்த்த வேண்டிய திசையின் பக்கமே வெட்டப்பட வேண்டியது ஏன்? 

விடைகள்:

i) மரத்தை வீழ்த்த வேண்டிய திசையில் அடியிலிருந்து செயல்படும் செங்குத்து விசை நீண்டநேரம் இருக்கக் கூடாது. 

ii) ஈர்ப்பு விசை ஒரு திருப்பு விசையை ஏற்படுத்த வேண்டும். 

iii) ஆகையால் மரமானது வெட்டி வீழ்த்த வேண்டிய திசையிலேயே வெட்ட வேண்டும். 

2. மூட்டை தூக்கும் தொழிலாளி மூட்டையை முதுகில் சுமக்கும் போது முன்னோக்கி சாய்வது ஏன்?  

விடைகள்:

1) மூட்டையை முதுகில் சுமக்கும் போது அவர் மீது விசை செயல்படும் ஈர்ப்பு மையம் உடலை விட்டு முன்னோக்கி செல்கிறது. 

ii) இது நிலையை தடுமாறச்செய்யும். 

iii) எனவே முன்னோக்கி குனியும் போது விசை செயல்படும் ஈர்ப்பு மையம் மனித உடலின் மேலே செயல்படுகிறது.

3. தீக்குச்சி ஒன்றை விரல் நுனியில் சமன் செய்வதை விட மீட்டர் அளவுகோள் ஒன்றை அதே போல் சமன் செய்வது எளிமையாக இருப்பது ஏன்? 

விடைகள்:

i) மீட்டர் அளவுகோலின் ஈர்ப்பு மையம், தீக்குச்சியின் ஈர்ப்பு மையத்தை விட செங்குத்தாக வைக்கும்போது உயரமாக உள்ளது. 

ii) ஈர்ப்பு மையம் புவியிலிருந்து குறைவான உயரத்தில் இருப்பதைவிட அதிக உயரத்தில் இருப்பதால் எளிதில் சமன் செய்து கொள்கிறது. 

iii) எனவே தீக்குச்சியை விட மீட்டர் அளவுகோலை சமநிலையில் வைப்பது எளிது.

4. இரு சமமான அளவு பாட்டில்களில் ஒன்றை நீர் நிரப்பியும் மற்றொன்றை காலியாகவும் கொண்டு சாய்தளத்தில் கீழ் நோக்கி உருளுமாறு அனுமதிக்கப்படு கிறது. இவற்றில் எது சாய்தளத்தின் அடிப்பகுதியை முதலில் அடையும்? விளக்குக.

விடைகள்: 

i) நீர் நிரப்பப்பட்ட பாட்டில் அடிப்பகுதியை முதலில் அடைகிறது.

ii). நிலைம திருப்புத்திறன் α 1 / கோண திசைவேகம் 

iii) காலியான பாட்டிலின் நிறை முழுவதும் அதன் மேற்பரப்பிலேயே பரவி இருக்கும். எனவே இதன் நிலைமத்திருப்புத்திறன் அதிகம், கோண திசைவேகம் குறைவு. ஆகையால் நீர் நிரப்பப்பட்ட பாட்டில் அடிப்பகுதியை முதலில் அடையும்.

5. கோண உந்தத்திற்கும் சுழற்சி இயக்க ஆற்றலுக்கும் இடையேயான தொடர்பை தருக. இவற்றிற்கு இடையேயான வரைபடத்தை வரைக. ஒத்த கோண உந்தம் கொண்ட இரு பொருட்களின் நிலைமத் திருப்புத்திறன்களை வரைபடம் மூலம் ஒப்பிடுக.

விடைகள்: 

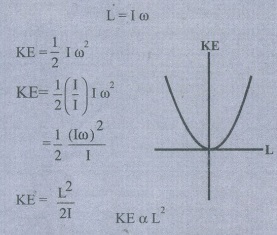
இது Y = Kx2 என்ற சமன்பாட்டை ஒத்திருப்பதால் வரைபடம் பரவளையம் ஆகும். 

இரு பொருட்களின் கோண உந்தம் சமம் எனில்

KE α 1/I

இயக்க ஆற்றல் குறைவாக உள்ள பொருளின் நிலைமத்திருப்புத்திறன் அதிகம்.

6. செவ்வக கட்டையானது மேசையின் மீது அமைதி நிலையில் உள்ளது. கட்டையை நகரச் செய்ய மேசையின் தளத்திலிருந்து h உயரத்தில் கிடைத்தள விசை செலுத்தப் படுகிறது. மேசை கட்டையின் மீது செலுத்தும் செங்குத்து விசை N, h ஐச் சார்ந்து இருக்குமா? 

விடைகள்:

i) செங்குத்து விசை h யை சார்ந்தது

ii) உயரத்தை பொருத்து ஈர்ப்பு விசை மாறுபடுவதால் செங்குத்து விசையும் h யை சார்ந்து இருக்கும். 

7. மூன்று சாய்தளங்களில் ஒரே மாதிரியான திண்மக் கோளங்கள் கீழ்நோக்கி இயங்குகிறது. சாய்தளங்கள் A, B, C ஆகியவை ஒத்த பரிமாணத்தை உடையன. Aயில் உராய்வின்றியும், B-இல் நழுவுதலற்ற உருளுதலும் மற்றும் C-யில் நழுவி உருளுதலும் ஏற்படுகிறது. சாய்தளத்தின் அடிப்பகுதியில் இவற்றின் இயக்க ஆற்றல்கள் EA EB EC இவற்றை ஒப்பிடுக.

விடைகள்:

● ஆற்றல் மாறா விதிப்படி நிலையாற்றல் பெற்றுள்ள இம்மூன்று கோளங்களும் இயக்க ஆற்றலை பெருகின்றன. 

● எனவே சாய்தளத்தில் அடிப்பகுதியில் இவற்றின் இயக்க ஆற்றல்கள் EA, EB மற்றும் EC சமமாக உள்ளது.

8. கீழ்க்கண்ட கூற்று தவறு எனக் காட்ட ஓர் உதாரணம் தருக. “ஏதேனும் இரு விசைகள் ஒன்றிணைந்து ஒரே தொகுபயன் விசையாக ஒரு பொருளின் மீது செயல்படும் போது, விசை ஒரே விளைவை கொடுக்கும்”. 

விடைகள்:

● ஒரு பொருளின் மீது செயல்படும் இரண்டு விசைகள் அவற்றுக்கிடையேயான கோணத்தை சார்ந்தது. 

● இரு சம ஒத்த விசைகள் எதிரெதிர் திசையில் செயல்பட்டால் தொகுபயன் விசை சுழி. 

● இரு சம விசைகள் ஒரே திசையில் செயல்பட்டால் தொகுபயன் விசை அதிகம்/இரு மடங்கு ஆகும். 

● எனவே ஏதேனும் இரு விசைகள் ஒன்றிணைந்து ஒரே தொகுபயன் விசையாக ஒரு பொருளின் மீது செயல்படும் போது விசை ஒரே விளைவை கொடுக்காது. 

(எகா) இருநபர்கள் காரைத் தள்ளுவது

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் இருபுள்ளி நிறைகளின் நிறை மையம்

எடுத்துக்காட்டு 5.1

3 kg, 5 kg என்ற இரு புள்ளி நிறைகள் X அச்சில் ஆதிப்புள்ளியிலிருந்து முறையே 4 m, 8 m என்ற தொலைவில் உள்ளன. இரு புள்ளி நிறைகளின் நிறை மையத்தின் நிலைகளை, 

(i) ஆதிப்புள்ளியிலிருந்தும் 

(ii) 3 kg நிறையிலிருந்தும் காண்க. 

தீர்வு

m1 = 3 kg, m2 = 5 kg என எடுத்துக் கொள்வோம்.

(i) ஆதிப்புள்ளியிலிருந்து நிறை மையத்தைக் கண்டறிதல்

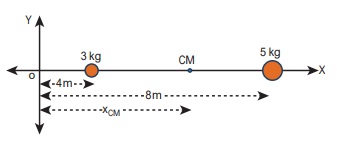
புள்ளி நிறைகள் X அச்சில் ஆதிப்புள்ளியிலிருந்து x1 = 4m, x2 = 8m என்ற தொலைவில் உள்ளன. எனவே நிறை மையம்.

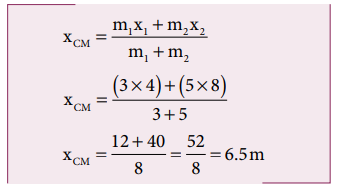
ஆதிப்புள்ளியிலிருந்து நிறை மையம் 6.5 m தொலைவில் அமைந்திருக்கும்.

(ii) 3 kg நிறையிலிருந்து நிறை மையத்தைக் கண்டறிதல் 

3 kg நிறையை ஆதிப்புள்ளிக்கு X அச்சில் இடமாற்றம் செய்வதாக கொள்வோம். ஆதிப்புள்ளியானது X அச்சில் 3 kg நிறையுள்ள இடத்தில் எடுத்துக் கொள்ளப்படுகிறது. எனவே 3 kg புள்ளி நிறையின் நிலை சுழியாகும் (x1 = O) மாற்றப்பட்ட ஆதிப் புள்ளியிலிருந்து 5 kg நிறை 4 m தொலைவில் உள்ளது. (x2 = 4m)

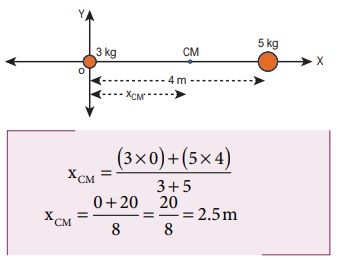
3 kg புள்ளி நிறையிலிருந்து 25 m தொலைவில் (5kg புள்ளி நிறையிலிருந்து 1.5 m தொலைவிலும்) நிறை மையம் அமைந்துள்ளது.

• இம்முடிவானது, நிறை மையம் அதிக நிறைக்கு அருகில் உள்ளதைக் காட்டுகிறது.

• ஆதிப்புள்ளி நிறைமையத்தில் அமையுமாறு கருதும்போது, திருப்புத் திறன்களின் தத்துவத்தை ஒத்து அமைகிறது.

m1 x1 = m2 x2; 3 × 2.5 = 5 × 1.5; 7.5 = 7.5

நிகழ்வு (i) யை (ii) உடன் ஒப்பிடும் போது 3 kg நிறையின் நிறைமையத்தினை 6.50 லிருந்து 4 m ஐக் கழிக்க Xcm = 25m எனவும் கண்டறியலாம் இது நிகழ்வு (i) இன் நிறைமையத்தின் நிலையிலேயே உள்ளது

எடுத்துக்காட்டு 5.2 

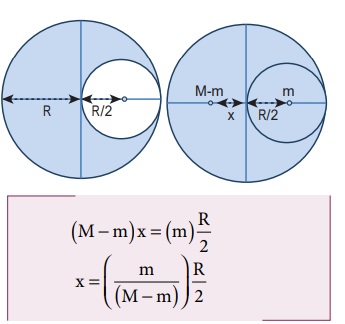
R ஆரமுடைய சீரான பரப்பு நிறை அடர்த்தி கொண்ட வட்டத்தட்டிலிருந்து R/2 ஆரமுடைய ஒரு சிறு தட்டு வடிவப் பகுதி படத்தில் காட்டியுள்ளவாறு வெட்டி எடுக்கப்படுகிறது. மீதமுள்ள பகுதியின் நிறை மையத்தைக் கணக்கிடுக. 

தீர்வு 

வெட்டப்படாத வட்டத்தட்டின் நிறையானது M என எடுத்துக் கொள்க. இதனுடைய நிறை மையமானது வட்டத்தட்டின் வடிவியல் மையத்தில் அமையும். இப்புள்ளியிலேயே ஆதிப்புள்ளியும் ஒருங்கமைகிறது.

வெட்டி எடுக்கப்பட்ட சிறு வட்டத்தட்டின் நிறை m என்க. (அதன் நிறை மையம் ஆதிப்புள்ளிக்கு) வலது புறத்தில் R/2 என்ற தொலைவில் படத்தில் காட்டியுள்ளவாறு அமைந்திருக்கும். 

எனவே வட்டத்தட்டின் மீதமுள்ள பகுதியின் நிறை மையம் ஆதிப்புள்ளிக்கு இடது புறத்தில் X தொலைவில் உள்ளதாக எடுத்துக் கொள்வோம். திருப்புத்திறன்களின் தத்துவத்திலிருந்து, கீழ்கண்டவாறு எழுத முடியும்.

பரப்பு நிறை அடர்த்தி 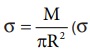என்பது ஓரலகு பரப்பின் நிறை) எனில், சிறிய வட்டத் தட்டின் நிறை (m) என்பது

மீதமுள்ள வட்டத் தட்டின் நிறை மையமானது வட்டத் தட்டின் மையத்திற்கு இடப்புறம் R/6 என்ற தொலைவில் இருக்கும்.

• பெரிய வட்டத்தட்டிலிருந்து பொதுவான மையத்தை (common centre) பொருத்து சிறிய பகுதி வெட்டியெடுக்கப்பட்டால் மீதமுள்ள வட்டத்தட்டின் நிறை மையம் எங்கு அமையும்?

எடுத்துக்காட்டு 5.3 

10 kg, 5 kg நிறையுடைய இரு புள்ளி நிறைகளின் நிலை வெக்டர்கள் முறையே 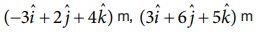ஆகும். நிறை மையத்தின் நிலையைக் கண்டறியவும். 

தீர்வு:

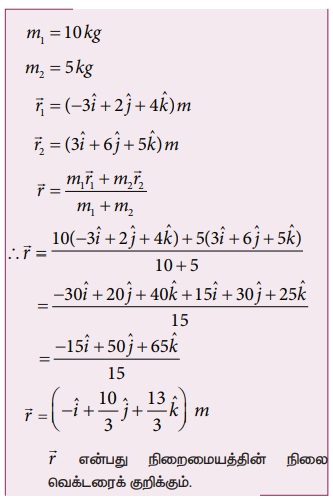
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் சீராகப் பரவியுள்ள நிறையின் நிறை மையம்

எடுத்துக்காட்டு 5.4 

M நிறையும் l நீளமும் கொண்ட சீரான நீள் அடர்த்தி கொண்ட (uniform rod) தண்டின் நிறை மையத்தைக் கண்க.

தீர்வு 

M நிறையும் l நீளமும் உடைய ஒரு சீரான நீள் அடர்த்தி கொண்ட தண்டினைக் (uniform rod) கருதுக. அதன் ஒரு முனை படத்தில் காட்டியுள்ள படி ஆதிப்புள்ளியுடன் ஒன்றியிருப்பதாக எடுத்துக்கொள்வோம். தண்டானது X அச்சில் வைக்கப்பட்டுள்ளது. தண்டினுடைய நிறை மையத்தைக் கண்டறிய, ஆதிப்புள்ளியிலிருந்து x தொலைவில் dx நீளமும் dm என்ற மீநுண் நிறையும் கொண்ட சிறுபகுதியை எடுத்துக் கொள்வோம். 

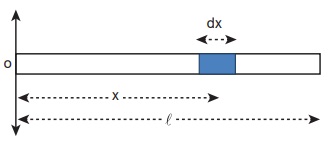
தண்டின் நீள் அடர்த்தி (ஓரலகு நீளத்திற்கான நிறை)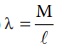

சிறிய பகுதியின் நிறை 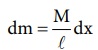தண்டின் நிறை மையத்திற்கான சமன்பாட்டை கீழ்க்கண்டவாறு எழுதலாம்.

நிலை l/2 என்பது தண்டின் வடிவியல் மையமாகும். இதிலிருந்து சீரான தண்டினைப் பொறுத்தவரை அதன் வடிவியல் மையத்திலேயே (Geometric centre) நிறை மையம் அமையும் என்ற முடிவிற்கு வரலாம்.

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் நிறை மையத்தின் இயக்கம்

எடுத்துக்காட்டு 5.5 

50 kg நிறையுள்ள ஒரு மனிதர் நிலையான நீரின் பரப்பில் மிதந்து கொண்டிருக்கும் 300 kg நிறையுடைய படகில் ஒரு முனையில் நின்று கொண்டிருக்கிறார். அவர் தரையில் நிலையாக உள்ள ஒருவரை பொருத்து படகின் மறுமுனையை நோக்கி 2ms-1 என்ற மாறாதிசைவேகத்தில் நடந்து செல்கிறார். (a) நிலையான உற்றுநோக்குபவரை பொருத்தும் (b) படகில் நடந்து கொண்டிருக்கும் மனிதரைப் பொருத்தும் படகின் திசைவேகம் என்ன?

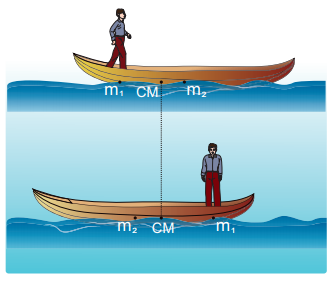
தகவல்: படகுக்கும் மனிதருக்கும் இடையே உராய்வு உள்ளது. ஆனால் படகுக்கும் நீருக்கும் இடையே உராய்வு கிடையாது.) 

தீர்வு 

மனிதரின் நிறை m1 = 50 kg 

படகின் நிறை m2 = 300 kg 

நிலையான உற்றுநோக்குபவரைப் பொருத்து: 

மனிதர் நகரும் திசைவேகம் v1 = 2 ms-1 மேலும் படகு நகரும் திசைவேகம் v2 (கண்டறியப்பட வேண்டியது) என்க.

(i) தரையில் நிலையாக உள்ள உற்றுநோக்குபவரைப் பொருத்து படகின் திசைவேகத்தைக் கணக்கிடுதல் 

அமைப்பின் மீது புறவிசைகள் செயல்படாதபோது, படகு - மனித அமைப்பின் அகவிசையாக செயல்படும் உராய்வின் காரணமாக மனிதன் - படகு அமைப்பு (boat - man system) இயங்குகிறது. ஆகவேநிறைமையத்தின் திசைவேகம் சுழியாகும் (vCM = 0). 

நிறை மையத்தின் சமன்பாடு (5.7) லிருந்து,

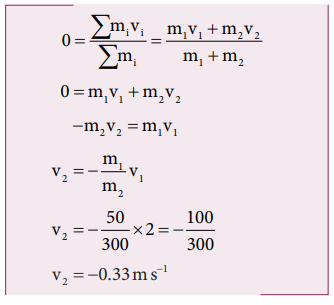
இங்கே, நிலையாக உள்ள உற்றுநோக்குபவருக்கு எதிர் திசையில் படகு செல்வதை எதிர்குறி காட்டுகிறது. 

(ii) நடக்கும் மனிதரைப் பொருத்து படகின் திசைவேகத்தைக் கண்டறிதல்: படகின் சார்புத் திசைவேகத்தை பின்வருமாறு கணக்கிடலாம்.

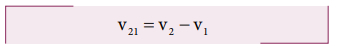
இங்கே, v21 என்பது நடக்கும் மனிதரைப் பொருத்து படகின் சார்புத் திசைவேகமாகும்

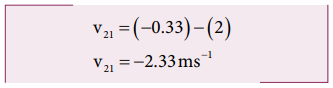
மனிதர் தன்னுடைய வலப்புறம் நகரும்போது படகு அவரின் இடது புறமாக நகர்வதை விடையில் உள்ள எதிர்குறி காட்டுகிறது.

• நடக்கும் மனிதனைப்பொருத்து படகின் சார்புத் திசைவேகத்தின் எண்மதிப்பானது, நிலையாக உற்று நோக்குபவரைப் பொருத்து படகின் சார்புத் திசைவேகத்தின் எண்மதிப்பை விட அதிகம்.

• நிலையாக உற்று நோக்குபவருக்கும் படகில் நடந்து செல்பவருக்கும் எதிர்திசையில் படகு இயங்குவதால் இரு விடைகளும் எதிர்குறியில் உள்ளன.

வெடித்தலின் நிறை மையம் 

ஓய்வு நிலையிலோ அல்லது சீரான இயக்கத்திலோ உள்ள பொருளின் அகவிசைகளினால் (internal forces) வெடித்தல் நடைபெறுகிறது எனில், அதன் நிறை மையத்தின் நிலை பாதிக்கப்படுவதில்லை. அது, அதே ஓய்வு நிலையிலோ அல்லது சீரான திசைவேகத்திலோ இருக்கும். ஆனால் வெடித்தபகுதிகளின் இயக்கவியல் அளவுகள் (kinematic quantities) பாதிக்கப்படும். வெடித்தலானது புறவிசைகளின் காரணமாக நிகழ்கிறது எனில் நிறைமையம், மற்றும் வெடித்த பகுதிகள் ஆகியவற்றின் இயக்கவியல் அளவுகள் பாதிக்கப்படும். 

எடுத்துக்காட்டு 5.6

5 kg நிறையுள்ள எறியமானது, (projectile) அது இயக்கத்தில் உள்ள போதே தானாக வெடித்து இரு கூறுகளாகப் பிரிகிறது. அதில் 3 kg நிறையுடைய ஒரு கூறானது, வீச்சின் நான்கில் மூன்று பங்கு 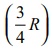தொலைவில் விழுகிறது. மற்றொரு கூறு எங்கு விழும்?

தீர்வு

புறவிசைகளின் துணையின்றி தானாக வெடிப்பதால் எறியத்தின் நிறை மையம் பாதிக்கப்படாது. மேலும் நிறைமையமானது தொடர்ந்து பரவளையப் பாதையிலேயே செல்லும். ஆனால் அதன் கூறுகளானது பரவளையப் பாதையை மேற்கொள்ளாது. கூறுகள் அனைத்தும் தரையில் விழும்போது நிறைமையம் எறியப்பட்ட புள்ளியிலிருந்து படத்தில் காட்டப்பட்டதுபோல் R தொலைவை (நெடுக்கம்) அடைகிறது. ஆகவே இறுதியில், படத்தில் காட்டியுள்ளபடி நிறை மையமானது எறி புள்ளியிலிருந்து R தொலைவில் (நெடுக்கம்) அமைந்திருக்கும்.

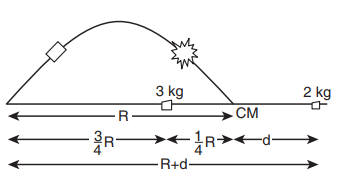
நிறைமையத்தின் இறுதி நிலையை ஆதி புள்ளியாக எடுத்துக் கொண்டால், திருப்புத்திறன்களின் தத்துவத்தின் படி

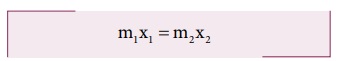
இங்கு, m1 = 3 kg, m2 = 2 kg, x1 = 1/4 R மற்றும் x2 = d என எடுத்துக் கொள்க. 

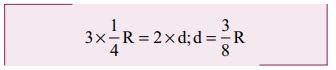
எறி புள்ளிக்கும் 2kg நிறை விழுந்துள்ள புள்ளிக்கும் இடையேயுள்ள தொலைவு R+d. 

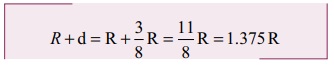
எனவே 2 kg நிறையுடைய மற்றொரு கூறானது எறிபுள்ளியிலிருந்து 1.375 R என்ற தொலைவில் விழுகிறது. (இங்கு R என்பது எறிபொருளின் கிடைத்தள நெடுக்கமாகும்)

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் திருப்பு விசை

எடுத்துக்காட்டு 5.7 

ஸ்பேனரின் கைப்பிடிக்கு செங்குத்தாக படத்தில் காட்டியுள்ளவாறு விசை செலுத்தப்படுகிறது. (i) திருகு மறை (Nut) யின் மையத்தைப் பொருத்து விசையின் திருப்பு விசை (ii) திருப்பு விசையின் திசை மற்றும் (ii) திருகு மறையைப் (Nut) பொருத்து திருப்பு விசை ஏற்படுத்தும் சுழற்சியின் வகை ஆகியவற்றைக் காண்க.

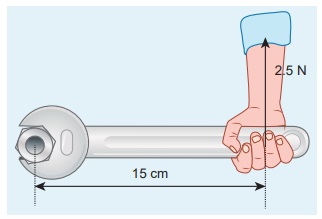
தீர்வு

ஸ்பேனரின் கைப்பகுதியின் நீளம், 

r = 15 cm = 15 × 10-2 m 

செலுத்தப்பட்ட விசை, F = 25N 

r க்கும் F க்கும் இடைப்பட்ட கோணம் θ = 90°

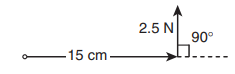
(i) திருப்பு விசை, τ θ = rF sinθ

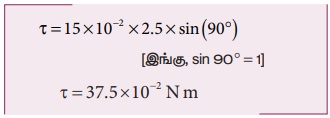
ii) வலக்கை விதிப்படி, திருப்பு விசையின் திசையானது தாளின் தளத்திலிருந்து வெளிநோக்கி அமைந்துள்ளது. 

(iii) திருப்பு விசை ஏற்படுத்திய சுழற்சி கடிகாரத்தின் திசைக்கு எதிர்திசையில் உள்ளது.

எடுத்துக்காட்டு 5.8

என்ற புள்ளியில் அமைந்த நிலை வெக்டரின் மீது செயல்படுகிறது. ஆதியைப் பொருத்து திருப்பு விசையின் மதிப்பை காண்க. 

தீர்வு

எடுத்துக்காட்டு 5.9 

பளு தூக்கி ஒன்றின் கரத்தின் நீளம் 20 m அக்கரமானது செங்குத்து அச்சோடு 30° கோணத்தில் நிறுத்தப்பட்டுள்ளது. 2 டன் எடையானது கரத்தால் தூக்கி நிறுத்தப்பட்டுள்ளது. பளு தூக்கியின் கரம் பொருத்தப்பட்ட நிலையான புள்ளியைப் பொருத்து புவியீர்ப்புவிசை ஏற்படுத்திய திருப்பு விசையைக் காண்க. 

[தகவல்: 1 டன் = 1000 kg; g = 10 ms-2, கரத்தின் எடை புறக்கணிக்கத்தக்கது]

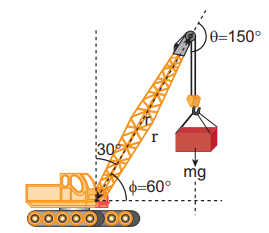
தீர்வு

தொங்கவிடப்பட்ட நிறையினால் ஏற்படும் விசை

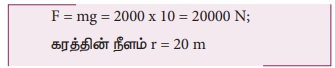
இந்த கணக்கிற்கு மூன்று வெவ்வேறு முறைகளில் தீர்வு காணலாம். 

முறை - I 

விசை F க்கும் கரத்தின் நீளம் r க்கும் இடையேயான கோணம் θ = 150°

பொருத்தப்பட்ட நிலை புள்ளியைப் பொருத்து கரத்தின் திருப்பு விசை

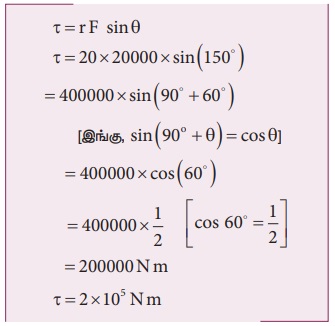
முறை-II 

விசையையும், பளுதூக்கியில் கரம் பொருத்தப்பட்ட புள்ளியிலிருந்து செங்குத்து தொலைவையும் கருதுவோம்

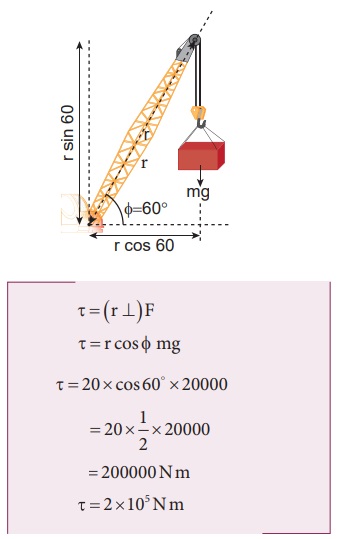
முறை III 

பளு தூக்கியின் கரம் பொருத்தப்பட்ட புள்ளியையும் செங்குத்து விசையையும் கருதுவோம்.

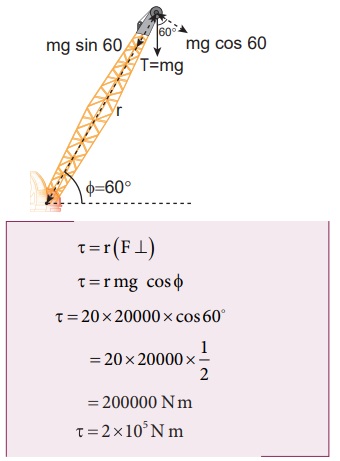
மூன்று முறைகளும் ஒரே தீர்வினை தருகிறது.

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் அச்சைப் பொருத்து திருப்பு விசை

எடுத்துக்காட்டு 5.10 

AB, OC, GH என்ற சட்டங்கள் ஒன்றுக்கொன்று செங்குத்தாக படத்தில் காட்டியுள்ளவாறு தரையில் நிலையாக பொருத்தப்பட்டுள்ளது. ஒரு கம்பி C என்ற புள்ளியில் கட்டப்பட்டுள்ளது. கம்பியின் தனித்த முனை D யானது விசை F இனால் இழுக்கப்படுகிறது. விசை உருவாக்கிய திருப்பு விசையின் எண் மதிப்பையும், திசையையும்

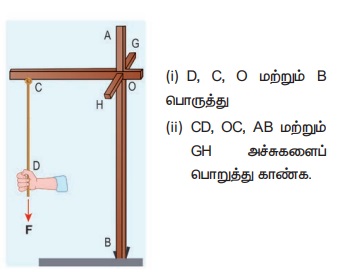
தீர்வு 

(i) D யைப் பொருத்து திருப்பு விசை சுழி. (D வழியாக F செயல்படுகிறது). 

C யைப் பொருத்து திருப்பு விசை சுழி. (C வழியாக F செயல்படுகிறது). 

O யைப் பொருத்து திருப்பு விசை 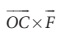(GH அச்சு வழியாக செயல்படுகிறது). 

B யைப் பொருத்து திருப்பு விசை 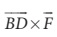(GH அச்சு வழியாக செயல்படுகிறது) 

(F -ஐப் பொருத்து B-யிலிருந்து செங்குத்து தொலைவு OC) 

(ii) CD யைப் பொருத்து திருப்பு விசை சுழி (F ஆனது CD க்கு இணை). 

OC யைப் பொருத்து திருப்பு விசை சுழி (OC யினை F ஆனது வெட்டிச் செல்கிறது). 

AB யைப் பொருத்து திருப்பு விசை சுழி (AB க்கு F இணையாகிறது). 

GH யைப் பொருத்து திருப்பு விசை 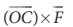(GH திசையில் அமையும்.)

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் கோணஉந்தம்

எடுத்துக்காட்டு 5.11

m நிறை கொண்ட துகளானது v என்ற மாறாத திசை வேகத்துடன் இயங்குகிறது. ஏதேனும் ஒரு புள்ளியைப் பொருத்து இயக்கம் முழுவதிலும் இதன் கோண உந்தம் மாறாதது எனக் காட்டுக.

தீர்வு 

m நிறை கொண்ட Q துகளானது மாறா திசைவேகம் யுடன் செல்வதாக கொள்வோம்.

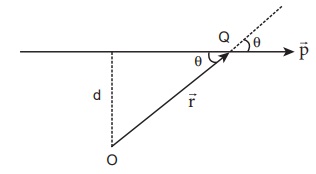
மாறா திசைவேகம் என்பதால் துகளின் பாதை நேர்க்கோட்டு பாதையாக அமையும். அதன் உந்தமும் 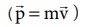அதே பாதையில் நேர்கோட்டில் அமையும். அப்பாதையிலிருந்து செங்குத்து தொலைவில் (d) ஆதிப்புள்ளி O வை எடுத்துக் கொள்வோம். ஒரு குறிப்பிட்ட கணத்தில் Q என்ற புள்ளியில் அமைந்த துகளின் நிலை வெக்டர் 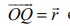என்க. ஒரு குறிப்பிட்ட கணத்தில் க்கும் க்கும் இடைப்பட்ட கோணம் θ என்க எனவே அக்கணத்தில் கோண உந்தத்தின் எண்மதிப்பு

இங்கு (OQ sinθ) என்பது ஆதிப்புள்ளிக்கும் பொருள் செல்லும் திசைக்கும் உள்ள செங்குத்துத் தொலைவு ஆகும். எனவே, துகள் Q வின் ஆதியைப் பொறுத்த கோண உந்தம்

மேற்கண்ட கோண உந்தத்தின் சமன்பாடு கோணம் θ வை பெற்றிருப்பதில்லை. நேர்கோட்டு உந்தம் p (p = m v) மற்றும் செங்குத்து தொலைவு d இரண்டும் மாறிலிகள். ஆதலால், துகளின் கோண உந்தமும் மாறாது. எனவே கோண உந்தமானது நேர்கோட்டு இயக்கத்தில் உள்ள பொருட்களோடும் தொடர்புடையது. பொருள் செல்லும் நேர்க்கோட்டு திசை, ஒருவேளை ஆதிப்புள்ளி வழியாகச் சென்றால் கோண உந்தம் சுழியாகவும், அது மாறாததாகவும் இருக்கும்.

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் திண்மப் பொருட்களின் சமநிலை

எடுத்துக்காட்டு 5.12

28 kg நிறையும் 10 m நீளமும் கொண்ட சீரான மரத்துண்டை அருண் மற்றும் பாபு சுமந்து செல்கின்றனர். மரத்துண்டின் முனைகளிலிருந்து இவர்கள் முறையே 1m மற்றும் 2m தொலைவில் பிடித்துள்ளனர். இவர்களில் யார் மரத்துண்டின் எடையை அதிகம் தாங்கிச் செல்கின்றார் [g=10ms-2]

தீர்வு 

மரத்துண்டானது இயந்திரவியல் சமநிலையில் உள்ளது எனக் கொள்க. அதன்படி மரத்துண்டின் மீது நிகர விசை மற்றும் நிகர திருப்பு விசையின் மதிப்பு சுழி. புவி ஈர்ப்பு விசையானது மரத்துண்டின் நிறைமையத்தில் கீழ் நோக்கி செயல்படும். அருண் மற்றும் பாபு முறையே A மற்றும் B புள்ளிகளில் செலுத்தும் RA, RB என்ற செங்குத்து விசைகள் கீழ்நோக்கிய புவியீர்ப்பு விசையை சமன் செய்கிறது. 

மரத்துண்டின் மொத்த எடை, W = mg = 28 × 10 = 280 N, ஆனது இருவராலும் தாங்கப்படுகிறது. மீள் செயல் விசையை இருவரும் தனித்தனியே அளிக்கின்றனர். மரத்துண்டின் மீது செயல்படும் அனைத்து விசைகளையும் தனித்த பொருளின் விசைப்படம் மூலம் காணலாம்.

இடப்பெயர்வு சமநிலையின் படி:

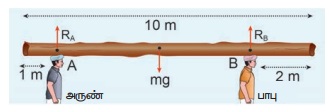
மரத்துண்டின் மீது செயல்படும் நிகர விசை சுழியாகிறது

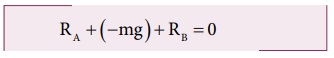
இங்கு, RA மற்றும் RB விசைகள் மேல் நோக்கிய நேர் குறியிலும். ஈர்ப்பியல் ஈர்ப்பு விசை (அல்லது எடை) கீழ்நோக்கி எதிர்குறியிலும் செயல்படுகிறது. 

RA + RB = mg 

சுழற்சி சமநிலையின் படி:

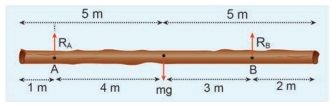
மரத்துண்டின் மீது செயல்படும் நிகர திருப்பு விசையின் மதிப்பு சுழியாகிறது. விசைகள் தொலைவிற்கு செங்குத்து என்பதால்,

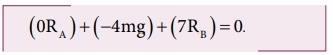
இங்கு, எதிர்வினை RA ஆனது தாங்கும் புள்ளி A யிலேயே செயல்படுவதால் A யைப் பொருத்து RA யின் திருப்புவிசை சுழியாகும். ஆனால் எடை mg யானது A யைப் பொருத்து கடிகார திசையிலும், எதிர்வினை RB ஆனது A யைப் பொருத்து எதிர் கடிகார திசையிலும் திருப்பு விசைகளை ஏற்படுத்தும்.

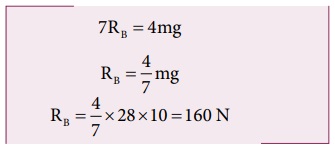
RB யின் மதிப்பை பிரதியிட, 

RA = mg - RB 

RA = 28 × 10 - 160 = 280 - 160 = 120 N 

RB ஆனது RA ஐ விட அதிகமாக இருப்பதால், பாபு அருணைவிட அதிக எடையை சுமக்கிறார்.

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் வட்டப்பாதையில் மிதிவண்டி ஒட்டுபவரின் சாய்வு இயக்கம்

எடுத்துக்காட்டு 5.13

20ms-1 என்ற திசைவேகத்துடன் வட்டப்பாதையில் மிதிவண்டி ஒட்டுபவர் செங்குத்து தளத்துடன் 30° கோணம் சாய்ந்த நிலையில் கடக்கிறார். வட்டப்பாதையின் ஆரம் என்ன? 

(g = 10 ms-2 எனக் கொள்க) 

தீர்வு: 

மிதிவண்டி ஒட்டுபவரின் திசை வேகம், v = 20 ms-1 

குத்தச்சுடன் கோணம் θ = 30° 

வட்டப்பாதையைக் கடக்க நிபந்தனை 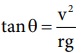மேற்கண்ட சமன்பாட்டை மாற்றி அமைக்க ஆரம் 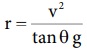ஐ பிரதியிட,

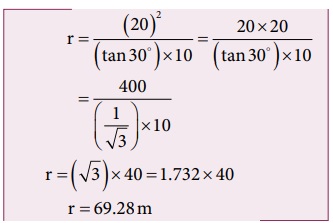
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் சீரான நிறை அடர்த்தி கொண்ட வட்டத்தட்டின் நிலைமத் திருப்புத்திறன்

எடுத்துக்காட்டு 5.14

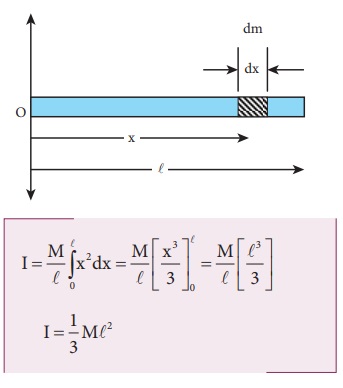
சீரான நிறை அடர்த்தி கொண்ட திண்மத்தண்டின் நிலைமத் திருப்புத்திறனை அதற்கு செங்குத்தாகவும் ஏதேனும் ஒரு முனையின் வழியே செல்லும் அச்சைப்பொருத்து காண்க.

தீர்வு 

நிலைமத் திருப்புத்திறனிற்கான கருத்துருவானது முந்தைய வருவித்தலின்படி தொகையீடு செய்து சமன்பாட்டைப் பெறலாம். இப்பொழுது திண்மத்தண்டின் இடது முனையினை ஆதியாகக் கொண்டு தொகையீடு காண எல்லையை 0 முதல் l எனக் கருதினால்,

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் சுழற்சி ஆரம்

எடுத்துக்காட்டு 5.15 

M நிறையும், R ஆரமும் கொண்ட வட்டத்தட்டு ஒன்றின் நிறை மையத்தின் வழியாகவும் அதன் தளத்திற்கு செங்குத்தாகவும் செல்லும் அச்சைப் பற்றிய சுழற்சி ஆரத்தைக் காண்க.

தீர்வு 

வட்டத்தட்டிற்கு செங்குத்தாகவும், நிறை மையம் வழியாகவும் செல்லும் அச்சைப் பற்றிய நிலைமத் திருப்புத்திறன் I = ½ MR2

இதனால் சுழற்சி ஆரம் என்பது பருப்பொருளின் வடிவியல் அம்சங்களான நீளம், அகலம், ஆரம் இவைகளோடு ஒன்றிணைந்து ஒரு நேர்க்குறி எண்ணின் பெருக்கல் பலனாக இருக்கும்.

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் நிலைமத் திருப்புத்திறனின் தேற்றங்கள்

எடுத்துக்காட்டு 5.16

3 kg நிறையும் 50 cm ஆரமும் கொண்ட வட்டத் தட்டு ஒன்றின் நிலைத்திருப்புத்திறனை பின்வரும் அச்சுகளைப் பொருத்து காண்க. 

(i) வட்டத்தட்டின் மையத்தில் தளத்திற்கு செங்குத்தாக செல்லும் அச்சு. 

(ii) வட்டத்தட்டின் பரிதியின் ஏதேனும் ஒரு புள்ளியின் வழிச்செல்வதும் தளத்திற்கு செங்குத்தானதுமான அச்சு. 

(iii) வட்டத்தட்டின் மையம் வழியாகவும் அதே தளத்திலேயே செல்வதுமான அச்சு, 

தீர்வு 

நிறை, M = 3 kg, ஆரம் R = 50 cm = 50 × 10-2 m = 0.5 m

(i) வட்ட தட்டின் மையத்தில் தளத்திற்கு செங்குத்தாக செல்லும் அச்சைப் பற்றிய நிலைமத்திருப்புத் திறன் (I) ஆனது.

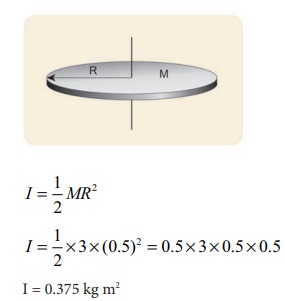
(ii) வட்டத்தட்டின் பரிதியில் ஏதேனும் ஒரு புள்ளி

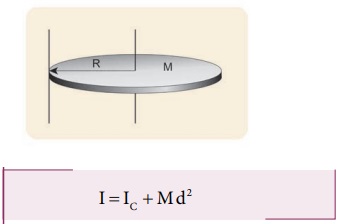
வழிச் செல்வதும் தளத்திற்கு செங்கத்தானதுமான அச்சைப் பற்றிய நிலைமத்திருப்புத்திறன் (I) யை இணையச்சு தேற்றத்தின் படி

இங்கு, IC = 1/2 MR2 மற்றும் d = R

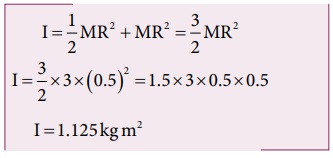
(ii) வட்டத்தட்டின் மையம் வழியாகவும் அதே தளத்திலேயே செல்வதுமான அச்சைப் பற்றிய நிலைமத்திருப்புத் திறனை, செங்குத்து அச்சு தேற்றத்தின் படி (I),

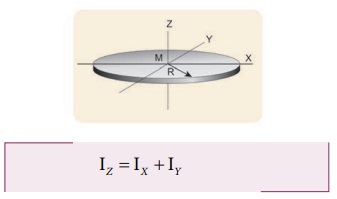
இங்கு Ix = Iy = I, மற்றும்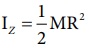  

எடுத்துக்காட்டு 5.17

கீழே படத்தில் காட்டப்பட்டுள்ள மெல்லிய தண்டினால் இணைக்கப்பட்டுள்ள இரு திண்மக் கோளங்களைக் கொண்ட அமைப்பின் நிலைமத் திருப்புத்திறனை அதன் வடிவியல் மையத்தை (Geometric centre) பொறுத்துக் காண்க.

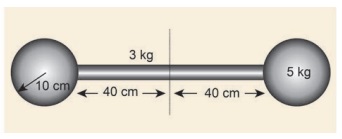
தீர்வு

மேலே காட்டப்பட்டிருக்கும் அமைப்பானது மூன்று பொருள்களால் ஆக்கப்பட்டிருக்கிறது. (ஒரு மெல்லிய தண்டு மற்றும் இரண்டு திண்மக் கோளம்) 

தண்டின் நிறை, M = 3kg மற்றும் 

தண்டின் நீளம், l = 80 cm = 0.8 m 

நிறைமையத்தைப் பொருத்து தண்டின் நிலைமத்திருப்புத் திறன்,

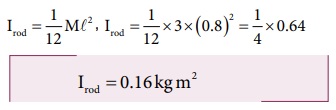
கோளத்தின் நிறை, M = 5 kg மற்றும் ஆரம், R = 10 cm = 0.1 m

நிறை மையத்தைப் பொருத்து கோளத்தின் நிலைமத்திருப்புத்திறன், 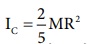அமைப்பின் வடிவியல் மையத்தைப் பொருத்து கோளத்தின் நிலைமத் திருப்புத்திறன்

I sph = I C + Md2

இங்கு, d = 40 cm + 10 cm = 50 cm = 0.5 m

இவ்வமைப்பானது இரு கோளங்களையும் தண்டினையும் பெற்றிருப்பதால் வடிவியல் மையத்தைப் பொருத்த நிலைமத்திருப்பத்திறன் (I) ஆனது, I = Irod + (2 × Isph) 

= (0.16) + (2 × 1.27) = 0.16 + 2.54 = 2.7kgm2

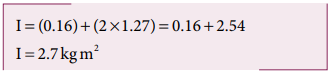
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் திண்மப் பொருட்களின் மீது திருப்பு விசையின் விளைவு

எடுத்துக்காட்டு 5.18

500g நிறையும் 10cm ஆரமும் கொண்ட வட்டத்தட்டு ஒன்று தன்னிச்சையாக படத்தில் காட்டப்பட்டது போல நிலையான அச்சைப் பொருத்துச் சுழல்கிறது. எடையற்ற மற்றும் மீட்சித்தன்மையற்ற கம்பியானது வட்டத்தின் விளம்பில் சுற்றுகள் சுற்றப்பட்டு மற்றொரு முணையானது 100g நிறையுடன் இணைக்கப்பட்டுள்ளது. 100g நிறையின் முடுக்கத்தை காண்க. (தகவல்: கம்பியானது வட்டத்தட்டின் விளிம்பில் நழுவவில்லை. மாறாக வட்டத்தட்டுடன் சுழல்கிறது g = 10 ms-2]

தீர்வு

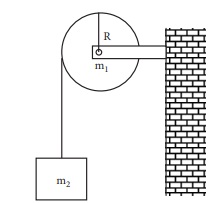
வட்டத்தட்டின் நிறையை m1 எனவும் அதன் ஆரத்தை R எனவும் கொள்க. தொங்கவிடப்பட்ட பொருளின் நிறை m2.

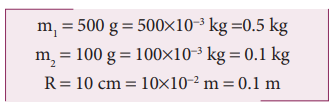
வட்டத்தட்டின் விளம்பில் பல முறை சுற்றப்பட்டுள்ள மிகக் குறைந்த நிறையுள்ள மற்றும் மீட்சியற்ற கம்பியானது நழுவுதல் இல்லாமல் வட்டத் தட்டுடன் சுழல்கிறது. நிறை m2 வின் தொடுகோட்டு முடுக்கமும் நிறை m1 இன் இடம்பெயர்வு முடுக்கமும் சமம் m1 மற்றும் m2 விற்கு தனித்தனியே தனித்த பொருளின் விசை (FBD) (Free Body Diagram) படத்தை வரைக.

வட்டத்தட்டிற்கான தனித்த பொருளின் விசைப்படம் (FBD) (Free Body Diagram)

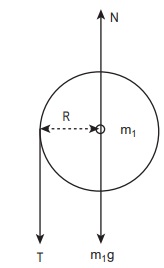
வட்டத்தட்டின் மீது செயல்படும் புவியீர்ப்பு விசை (m1g) ஆனது கீழ்நோக்கியும் வட்டத்தட்டானது மையத்தில் பொருத்தப்பட்டுள்ள மையப் புள்ளியின் வழியாக செங்குத்து விசை (N) யும் செயல்படுகிறது. வட்டத்தட்டின் பரிதியில் சுழலும் அச்சிற்குச் செங்குத்தாகக் கீழ்நோக்கி இழுவிசை T செயல்படுகிறது. மேலும் புவியீர்ப்பு விசையும் (m1g) யும் செங்குத்து விசைNம் ஒன்றை ஒன்று சமன்செய்கிறது. m1g = N 

இழுவிசை T ஆனது திருப்பு விசையை (R T) அளிப்பதால் வட்டத்தட்டானது கோண முடுக்கம் 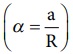வுடன் சுழற்சி இயக்கத்திற்கு உட்படுகிறது. இங்கு a என்பது வட்டத்தட்டின் விட்டத்தில் உள்ள புள்ளி தொடுவியல் திசையில் உணரும் நேர்கோட்டு முடுக்கமாகும். இவ்வட்டத்தட்டின் நிலைத்திருப்புத்திறன் I மற்றும் இதன் சுழற்சி ஆரம் K எனில்

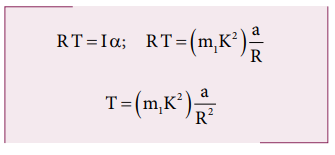
கம்பியின் ஒரு முனையில் கட்டப்பட்ட நிறையின் தனித்த பொருளின் விசைப்படம் (FBD) 

இதன் புவியீர்ப்பு விசை (m2g) கீழ்நோக்கிச் செயல்படுகிறது மற்றும் இழுவிசை T மேல்நோக்கி செயல்படுகிறது. இவற்றின் தொகு பயன் விசை நிறையின் மீது கீழ்நோக்கிச் செயல்படுகிறது. (T < m2g)

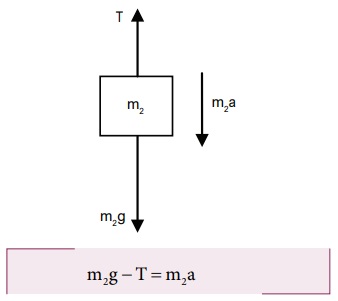
வட்டத்தட்டினால் செயல்படும் இழுவிசை T யை பிரதியிட

என்ற சமன்பாடு வட்டத்தட்டின் தளத்திற்கு செங்குத்தாகவும் மையம் வழிச் செல்லும் அச்சைப் பற்றி சுழல்வதால் பிரதியிட்டு சுருக்க, 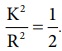முடுக்கத்திற்கான சமன்பாடு கீழ்க்கண்டவாறு கிடைக்கும்.

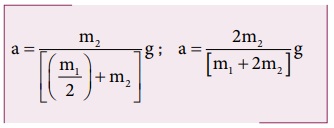
மதிப்புகளைப் பிரதியிட,

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் கோணஉந்த மாறா விதி

எடுத்துக்காட்டு 5.19

ω கோணத் திசைவேகத்துடன் சுழலும் வட்ட மேசையின் மீது சர்க்கஸ் வீரர் ஒருவர் கைகளை நீட்டிய நிலையில் உள்ளார். அவர் கைகளைத் தன்னை நோக்கி உட்புறமாக மடக்கும் போது நிலைமத்திருப்புத் திறனானது ஆரம்ப மதிப்பிலிருந்து மூன்றில் ஒரு பங்காகக் குறைகிறது. அவரது புதிய நிலையில் கோண திசை வேகத்தை காண்க. (தகவல் - புறத்திருப்பு விசை செயல்படாத நிலையில்) 

தீர்வு 

கைகள் நீட்டப்பட்ட நிலையில் சர்க்கஸ் வீரரின் நிலைமத்திருப்புத்திறன் I என்க. சர்க்கஸ் வீரரின் மீதும் சுழல்மேசை மீதும் திருப்பு விசை எதுவும் செயல்படாத நிலையில் கோண உந்தம் மாறாது எனவே கோண உந்தத்தின் சமன்பாடானது.

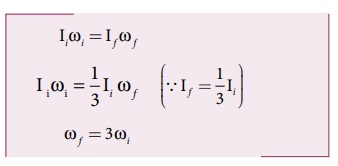
மேற்கண்ட முடிவிலிருந்து ஆரம்பக் கோணத் திசைவேகமானது மூன்று மடங்கு அதிகரித்துள்ளது என்பது தெளிவாகிறது.

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் சுழற்சி இயக்கத்தின் இயக்க ஆற்றல்

எடுத்துக்காட்டு 5.20

9 kg நிறையும் 3 m ஆரமும் கொண்ட வளையமானது, அந்த வளையத்தின் தளத்திற்கு செங்குத்தாகவும், மையம் வழிச் செல்லும் அச்சைக் பற்றி 240 rpm வேகத்தில் சுழலும்போது அது பெற்றுள்ள சுழல் இயக்க ஆற்றலை கணக்கிடுக. 

தீர்வு 

பொருளின் சுழல் இயக்க ஆற்றல்,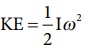

வளையத்தின் நிலைமத்திருப்புத்திறன் I = MR2

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் நழுவுதலும் சறுக்குதலும் உருளும் இயக்கம்

எடுத்துக்காட்டு 5.21

உருளும் சக்கரம் ஒன்றின் நிறை மையமானது 5 m s-1 திசைவேகத்துடன் இயங்குகிறது. இதன் ஆரம் 1.5m மற்றும் கோண திசைவேகம் 3 rad s-1, இச்சக்கரம் நழுவுதலற்ற உருளுதலில் உள்ளதா என சோதிக்க?

தீர்வு 

இடம்பெயர்வு திசைவேகம் (VTRANS) அல்லது நிறை மையத்தின் திசைவேகம்

VCM = 5 ms-1

ஆரம், R = 1.5 m மற்றும் கோண திசைவேகம் ω = 3 rad s-1

சுழற்சி திசைவேகம், VROT = R ω

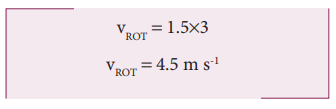
எனவே VCM> Rω. அல்லது VTRANS > Rω. இந்த இயக்கமானது நழுவுதலற்ற உருளுதல் இல்லை மாறாக சறுக்குதல் இயக்கத்தில் உள்ளது.

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் நழுவுதலற்ற உருளுதலின் இயக்க ஆற்றல் (உருளும் இயக்கம்)

எடுத்துக்காட்டு 5.22

திண்மக் கோளம் ஒன்று நழுவுதலற்ற உருளுதலில் உள்ளது. அதன் இடப்பெயர்ச்சி இயக்க ஆற்றலுக்கும், சுழற்சி இயக்க ஆற்றலுக்கும் இடையேயான விகிதம் என்ன?

தீர்வு 

நழுவுதலற்ற உருளுதலின் மொத்த ஆற்றலுக்கான சமன்பாடு,

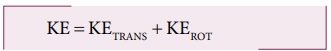
மொத்த இயக்க ஆற்றலுக்கான சமன்பாடுகளிலிருந்து (5.58) மற்றும் (5.59),

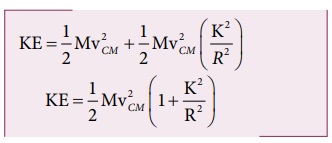
என்பதால்,

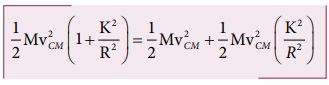
மேற்கண்ட சமன்பாட்டிலிருந்து நழுவுதலற்ற உருளுதலின் மொத்த இயக்க ஆற்றலிற்கும் இடப்பெயர்ச்சி மற்றும் சுழற்சி இயக்க ஆற்றலிற்கும் இடையேயான தகவு

தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள் சாய்தளத்தில் உருளுதல்

எடுத்துக்காட்டு 5.23

நான்கு உருளை வடிவ பொருட்களான வளையம், வட்டத்தட்டு, உள்ளீடற்ற கோளம் மற்றும் திண்மக் கோளம் ஆகியவை ஒத்த ஆரம் R உடன் ஒரே நேரத்தில் சாய்தளத்தில் உருள ஆரம்பிக்கிறது. எந்த பொருள் சாய்தளத்தின் அடிப்பகுதியை முதலில் வந்தடையும் என்பதைக் காண்க. 

தீர்வு 

வளையம், வட்டத்தட்டு, உள்ளீடற்றக் கோளம் மற்றும் திண்ம கோளம் ஆகிய நான்கின் சுழற்சி ஆரங்கள் K ஆனது 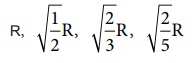(அட்டவணை (5.3) இன்படி இதன் எண்வடிவு முறையே 1R, 0.707 R, 0.816 R, 0.632 R ஆகும். 

நேரத்திற்கான சமன்பாடு

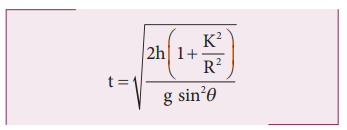
சுழற்சி ஆரம் குறைவாகப் பெற்றுள்ள பொருள் அடிப்பகுதியை அடைய குறைந்த நேரத்தை எடுத்துக் கொள்ளும். சாய்தளத்தில் பொருட்கள் வந்தடையும் வரிசை: முதலில் திண்மக்கோளம், இரண்டாவது வட்டத்தட்டு, மூன்றாவது உள்ளீடற்ற கோளம், நான்காவது வளையம் என அமையும்.