விசையும் இயக்கமும் | முதல் பருவம் அலகு 2 | 7 ஆம் வகுப்பு அறிவியல் - மாணவர் செயல்பாடு | 7th Science : Term 1 Unit 2 : Force and Motion
7 ஆம் வகுப்பு அறிவியல் : முதல் பருவம் அலகு 2 : விசையும் இயக்கமும்
மாணவர் செயல்பாடு
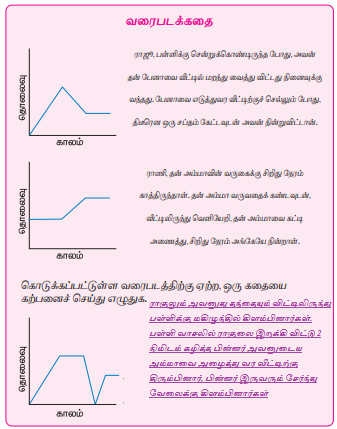
கீழே கொடுக்கப்பட்டிருக்கும் படத்தைப் பார். படத்தில் காட்டப்பட்டுள்ளபடி, கவிதா தனது வீட்டிலிருந்து இரு வழிகளில் பள்ளிக்குச் செல்ல முடியும். எப்பாதையின் வழியாகச் சென்றால் அவளால் விரைவில் பள்ளியை அடைய இயலும் என உங்களால் கூற இயலுமா?
பாதை - A (1.5 km)
பாதை - B (2 km)
பாதை - A பதில்
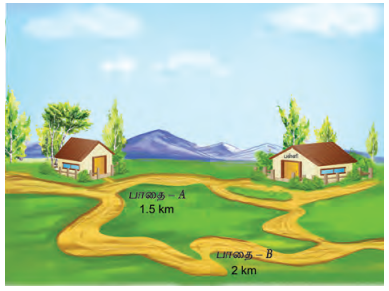
கீழே கொடுக்கப்பட்டுள்ள படத்தில், இலை ஒன்று மரத்திலிருந்து கீழே விழுவதைக் காணலாம். எந்தப் பாதையின் வழியாகக் கீழே விழும்போது இலை தரையை வேகமாக வந்தடையும்? பாதை அ
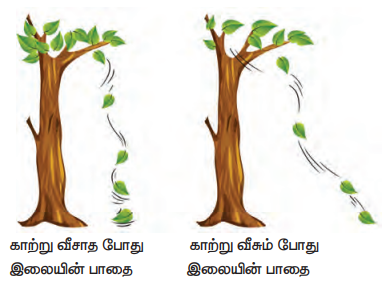
உமாவும், பிரியாவும் ஒரே பள்ளியில் படிக்கும் தோழிகள். அவர்கள் இருவரும் பள்ளி நேரம் முடிந்தவுடன் அருகில் உள்ள விளையாட்டுத் திடலுக்குச் சென்று விளையாடிவிட்டு வீடு திரும்புவார்கள். ஒருநாள் உமா தனது பாட்டி வீட்டிற்குச் சென்றுவிட்டு, திடலுக்கு வருவதாகக் கூறிச் சென்றாள். இருவரும் விளையாட்டுத் திடலுக்குச் சென்ற பாதை படத்தில் காட்டப்பட்டுள்ளது.
ஒரு நூலினை எடுத்துக்கொண்டு, படத்தில் காட்டப்பட்டுள்ள பாதையின் (அ மற்றும் ஆ) நீளங்களை அளக்கவும். எப்பாதையின் நீளம் அதிகமாக உள்ளது? பாதை ஆ
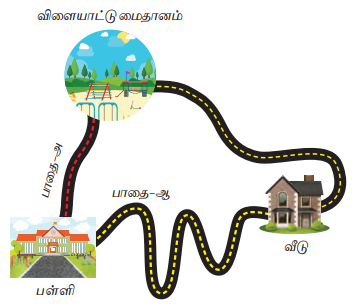
மேற்கண்ட நிகழ்வுகளிலிருந்து ஒரு பொருளானது ஓர் இடத்திலிருந்து மற்றோர் இடத்திற்குச் செல்லும்போது அவ்விரு இடங்களையும் இணைக்கும் நேர்க்கோட்டுப் பாதையில் சென்றால் விரைவில் அவ்விடத்தினைச் சென்றடையலாம் என நாம் அறிகிறோம். இந்த நேர்கோட்டுப்பாதையே இரு புள்ளிகளுக்கு இடையிலான மிகக் குறைந்த தொலைவு ஆகும்.
இப்பாடத்தில், தொலைவு மற்றும் இடப்பெயர்ச்சி, வேகம் மற்றும் திசைவேகம், வேகம் - காலம் வரைபடம், திசைவேகம் - காலம் வரைபடம், ஈர்ப்பு மையம் மற்றும் நிலைத்தன்மை ஆகியவை குறித்து பார்க்க இருக்கிறோம்.ஒருவர் A என்ற இடத்திலிருந்து B என்ற இடத்திற்கு மேற்கொள்ளும் இயக்கத்தை கீழே உள்ள படம் காண்பிக்கிறது.
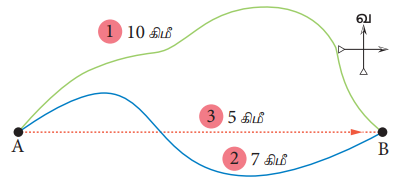
இதில் முதல் பாதையின் வழியாக அவர் 10 கிமீ தூரம் பயணிக்கிறார். இரண்டாவது பாதையின் வழியாக பயணம் செய்யும் போது 7 கிமீ தூரம் பயணிக்கிறார். முதல் பாதையில் A க்கும் Bக்கும் இடைப்பட்ட தூரம் 10 கிமீ. இரண்டாவது பாதையில் அவற்றிற்கு இடைப்பட்ட தூரம் 7 கிமீ. இரண்டு புள்ளிகளுக்கும் இடையே உள்ள மிகக்குறைந்த தூரம் 5 கிமீ. இது மூன்றாவது பாதையால் குறிக்கப்படுகிறது. எனவே, எந்தப் பாதையில் அவர் பயணம் செய்தாலும் அவரது இடப்பெயர்ச்சி 5 கிமீ (கிழக்குத் திசையில்) ஆகும்.
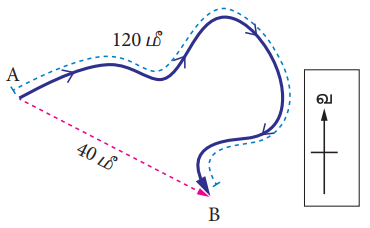
A என்ற புள்ளியிலிருந்து B என்ற புள்ளிக்குப் பயணம் செய்யும் ஒரு பொருளின் பாதையானது படத்தில் காட்டப்பட்டுள்ளது. அப்பொருள் பயணம் செய்த மொத்தத் தொலைவு 120 மீ மற்றும் அதன் இடப்பெயர்ச்சி 40 மீ (தென்கிழக்குத் திசையில்) ஆகும்.
முயல் ஒன்று ஓடிய பாதை கீழே உள்ள படத்தில் காட்டப்பட்டுள்ளது. ஒவ்வொரு கட்டத்தின் பரப்பளவும் ஒரு சதுர மீட்டர் எனக் கொள்வோம். முயல் A என்ற புள்ளியிலிருந்து ஓடத் துவங்கி B என்ற புள்ளியை வந்தடைகிறது. எப்பொழுது அது கடந்த தொலைவும், இடப்பெயர்ச்சியும் சமமாக இருக்கும்? (முயல் ஓடத் துவங்கிய புள்ளியும், முடித்த புள்ளியும் வெவ்வேறாக இருக்க வேண்டும்).
நேர் கோட்டு பாதையில் பயணிக்கும் போது கடந்த தொலைவும், இடப்பெயர்ச்சியும் சமமாக இருக்கும்
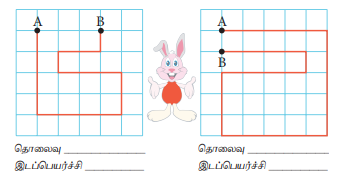
தொலைவு 17 மீ தொலைவு 3 மீ
இடப்பெயர்ச்சி 27 மீ இடப்பெயர்ச்சி 1மீ
நாம் ஒரு பொருளின் இடப்பெயர்ச்சியைக் குறிப்பிடும் போது அது பயணம் மேற்கொள்ளும் திசையைப் பொருத்து நேர்குறி அல்லது எதிர்குறியைப் பயன்படுத்துகிறோம்.

இங்கு பொருளின் ஆரம்ப நிலையை A எனக் கொள்வோம். பொருள் A என்ற புள்ளியிலிருந்து B என்ற புள்ளிக்குச் செல்லும்போது இடப்பெயர்ச்சி நேர்குறியையும், B என்ற புள்ளியிலிருந்து A என்ற புள்ளிக்குச் செல்லும்போது எதிர்குறியையும் பெறுகிறது.
சுபா தன் வீட்டிலிருந்து அருகில் உள்ள மைதானத்திற்குச் செல்கிறாள். கீழே உள்ள படத்தைப் பார்த்து, பின்வரும் வினாக்களுக்கு விடையளி.
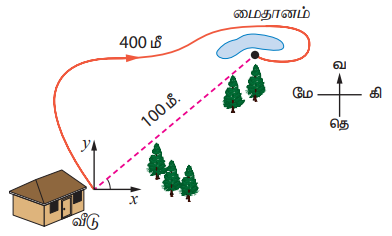
1. அவள் பயணம் செய்த தொலைவு என்ன?
2. அவளின் இடப்பெயர்ச்சி என்ன?
பின்வரும் வினாக்களுக்கு உன்னால் விடையளிக்க முடியுமா?
❖ ஒரு பொருள் கடந்த தொலைவு 15 கிமீ அப்பொருளின் இடப்பெயர்ச்சி 15 கிமீ. இவற்றிலிருந்து நீ அறிவது என்ன?
❖ ஒருவர் பயணம் செய்த தொலைவு 30 கிமீ அவரின் இடப்பெயர்ச்சி 0 கிமீ எனில் நீ அறிவது என்ன?
நாட்டிகல் மைல்
வான் மற்றும் கடல் வழிப் போக்குவரத்துகளில் தொலைவினை அளவிடப் பயன்படுத்தப்படும் அலகு நாட்டிகல் மைல் ஆகும். ஒரு நாட்டிகல் மைல் என்பது 1.852 கி.மீ ஆகும்.
கப்பல் மற்றும் விமானங்களின் வேகத்தை அளவிடப் பயன்படும் அலகு நாட் எனப்படும். அவை ஒரு மணி நேரத்தில் ஒரு நாட்டிகல் மைல் தொலைவை கடக்கின்றன என்பதை இது குறிக்கிறது.
கீழே கொடுக்கப்பட்டுள்ள படத்தைப் பார். ஒரு ஓட்டப்பந்தய வீரர் 25 விநாடியில் 200 மீட்டர் தூரத்தினை நிறைவு செய்கிறார். அவரின் வேகம் மற்றும் திசைவேகத்தினைக் காண்க.
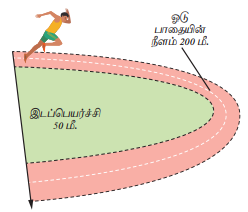
வேகம் = கடந்த தொலைவு / காலம்
= 200 / 25
= 8 மீ/வி
திசைவேகம் = இடப்பெயர்ச்சி / காலம்
= 50 / 25
= 2 மீ/வி
கீழே கொடுக்கப்பட்டுள்ள படத்தில் ஒரு மகிழுந்தானது கிழக்குத் திசையில் 5 கிமீ தூரம் பயணம் செய்கிறது. பின்னர், திரும்பி அதே பாதையில் மேற்கு நோக்கி 7 கிமீ தூரம் பயணம் செய்கிறது. இப்பயணத்தினை நிறைவு செய்ய அது 0.2 மணி நேரம் எடுத்துக்கொள்கிறது எனில் அதன் சராசரி திசைவேகத்தினைக் காண்க.
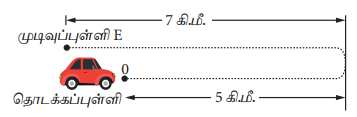
சராசரி திசைவேகம் = மொத்த இடப்பெயர்ச்சி / எடுத்துக்கொண்ட மொத்தக் காலம்
(0 என்ற புள்ளியிலிருந்து கிழக்குத் திசை நேர்குறியாக எடுத்துக்கொள்ளப்படுகிறது)
= (5-7) / 0.2
=-2 / 0.2
= - 10 கி.மீ / மணி அல்லது – 10 × 5 / 18
= - 25 / 9 = - 0. 28 மீ / வி
பின்வரும் வினாக்களுக்கு விடையளி
❖ சீரான திசைவேகத்தில் 100 மீ தொலைவினை 4 விநாடிகளில் கடக்கும் மகிழுந்தின் திசைவேகத்தைக் கண்டறிக.
திசைவேகம் = தொலைவு / நேரம்
= 100/4 = 25 மீ/வி
❖ உசைன் போல்ட் 100 மீ தூரத்தினை 9.58 விநாடிகளில் கடக்கிறார். அவரது வேகத்தினைக் கண்டறிக. 30 மீ/வி வேத்தில் ஓடக்கூடிய சிறுத்தையுடன், உசைன் போல்ட் ஓட்டப்பந்தயத்தில் கலந்து கொண்டால் வெற்றி பெறுவது யார்?
உசைன் போல்டின் வேகம் = 100 மீ
சிறுத்தையின் வேகம் = 30 மீ/வி
வெற்றி பெறுவது சிறுத்தை
❖ 4 மீ கிழக்கு நோக்கி நேராக நடந்து, பின்னர் 2 மீ தெற்கு நோக்கியும், அடுத்து 4 மீ மேற்கு நோக்கியும், கடைசியாக 2 மீ வடக்கு நோக்கியும் நீ நடக்கிறாய் எனக் கொள்வோம். மொத்த தூரத்தினை 24 விநாடிகளில் நீ கடக்கிறாய். உனது சராசரி வேகம் எவ்வளவு? சராசரி திசைவேகம் எவ்வளவு?
மொத்த தூரம் = 12 மீ
மொத்த நேரம் = 24 வி
சராசரி திசைவேகம் = மொத்த இடப்பெயர்ச்சி / எடுத்துக்கொண்ட மொத்தக் காலம்
= 12/24 = 0.5 மீவி
சராசரி வேகம் = 0 மீவி
12 / 24 = 0.5 மீவி
தொடக்க புள்ளியும் இறுதிப் புள்ளியும் ஒன்றாக இருப்பதால் சராசரி வேகம் பூஜ்ஜியமாகும்
இடப்பெயர்ச்சி பூஜ்ஜியமாகும், சராசரி வேகம் உள்ளது
சராசரி திசைவேகம் = மொத்த இடப்பெயர்ச்சி / எடுத்துக்கொண்ட மொத்தக் காலம்
ஓய்வுநிலையில் உள்ள ஒரு மகிழுந்தானது, நேர்கோட்டில் இயங்கத் தொடங்குகிறது எனக் கொள்வோம். அது 4 விநாடிகளில் 12 மீ / வி வேகத்தினை அடைகிறது எனில் அதன் முடுக்கத்தினைக் கணக்கிடுக (மகிழுந்து சீரான முடுக்கத்தில் உள்ளது எனக் கொள்க).
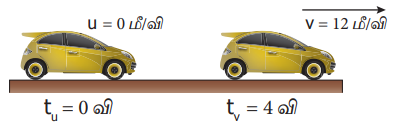
ஆரம்பத் திசைவேகம் (u) = 0 மீ / வி
இறுதி திசைவேகம் (v) = 12 மீ / வி
எடுத்துக்கொண்ட நேரம் (t) = 4 வி
முடுக்கம் (a) = (v-u) / t
= (12-0) / 4
= 3 மீ/வி2
நேர் முடுக்கம்
ஒரு பொருளின் திசைவேகமானது காலத்தினைப் பொருத்து அதிகரித்துக் கொண்டே சென்றால் அப்பொருளில் ஏற்படும் முடுக்கம் நேர் முடுக்கம் எனப்படும்.

நான் எவ்வளவு வேகமானவன் பாருங்கள்!

என் பெயர் சிறுத்தை. நான் மிகவேகமாக ஓடக்கூடிய விலங்கு. எனது வேகம் என்ன தெரியுமா? அது, 25 மீ / வி முதல் 30 மீ / வி வரை ஆகும். என்னால் இரண்டு விநாடியில் எனது வேகத்தினை 0 விலிருந்து 20 மீ/வி ஆக மாற்றிக் கொள்ளமுடியும். எனது முடுக்கம் வியப்பாக உள்ளது அல்லவா ! அதை நீங்கள் கணக்கிட முடியுமா?
எதிர் முடுக்கம்
ஒரு பொருளின் திசைவேகமானது காலத்தினைப் பொருத்து குறைந்து கொண்டே வந்தால் அப்பொருளில் ஏற்படும் முடுக்கம் எதிர்முடுக்கம் எனப்படும்.
ஒரு நேர்கோட்டுப் பாதையில் 8 மீ/வி என்ற திசைவேகத்தில் இயங்கிக்கொண்டிருக்கும் பந்தானது 10 விநாடியில் 2 மீ/வி என்ற திசைவேகத்தினை அடைகிறது. அப்பொருள் பெறும் எதிர்முடுக்கம் யாது? (அது சீரான எதிர்முடுக்கத்தைக் கொண்டுள்ளதாகக் கொள்க).
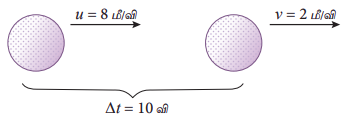
ஆரம்பத் திசைவேகம் (u) = 8 மீ/வி
இறுதித் திசைவேகம் (v) = 2 மீ/வி
எடுத்துக்கொண்ட நேரம் (t) = 10 வி
முடுக்கம் (a) = (v - u) / t
= (2-8) / 10
= - 0.6 மீ/வி2
ஒரு பேருந்தின் சீரான முடுக்கம் கீழ்க்காணும் அட்டவணையில் கொடுக்கப்பட்டுள்ளது.
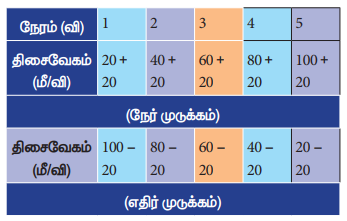
இங்கு பொருளின் திசைவேகமானது 20 மீ/வி என்ற வீதத்தில் மாற்றம் அடைவதால் (அதிகரித்தல் அல்லது குறைதல்) அதன் முடுக்கம் 20 மீ/வி2 ஆகும். அப்பொருளின் திசைவேகம் 20 மீ/வி என்ற வீதத்தில் குறைந்தால், அதன் எதிர்முடுக்கம் 20 மீ/வி2 ஆகும்.
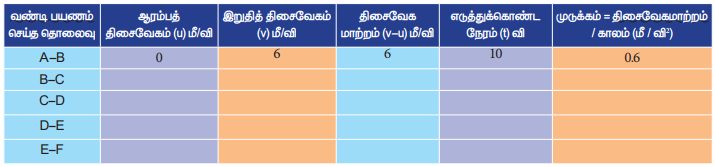
ஒரு தொடர்வண்டி நேர்கோட்டில் பயணம் செய்யும் பாதையை கீழே உள்ள படமானது காட்டுகிறது. படத்தினைப் பார்த்து அட்டவணையைப் பூர்த்தி செய்யவும்.

விடை :
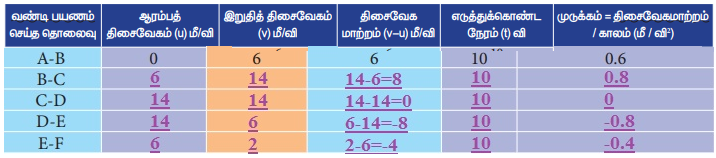
ஆய்வு
தொடர்வண்டி A முதல் B மற்றும் B முதல் C வரையிலான தூரத்தை கடக்கும் போது அது வேகமாக இயங்கும்
இது CD தூரத்தை கடக்கும் போது முடுக்கம்(i.e) சீரான வேகம் இல்லை
அது D இலிருந்து E முதல் F வரையிலான தூரத்தை கடக்கும் போது அது எதிர்மறை முடுக்கம் அல்லது குறைதல்
அல்லது பின்னடைவாக உள்ளது. (அதாவது) அதன் வேகம் பொறுத்து குறைகிறதுO என்ற புள்ளியிலிருந்து புறப்பட்டுச் செல்லும் மகிழுந்து ஒன்று கீழே உள்ள படத்தில் காட்டப்பட்டுள்ளது. ஒவ்வொரு விநாடி நேரத்திலும் அது கடக்கும் தொலைவானது அளக்கப்படுகிறது. அதன் தொலைவு மற்றும் காலம் பதிவு செய்யப்பட்டு அதற்கான வரைபடமானது வரையப்படுகிறது. இந்நிகழ்வில் காணப்படும் நான்கு சாத்தியக்கூறுகள் கீழே கொடுக்கப்பட்டுள்ளன.
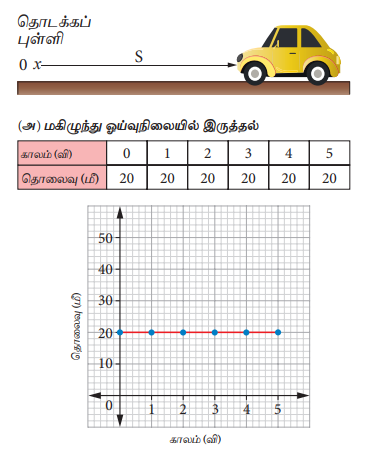
இந்த வரைபடத்தில், நேர்கோட்டின் சாய்வு சுழி மதிப்பினைப் பெற்றுள்ளது. அதாவது, ஒவ்வொரு விநாடியிலும் தொலைவானது மாறாமல் உள்ளது எனவே, மகிழுந்து ஓய்வு நிலையில் உள்ளது.
(ஆ) மகிழுந்து 10 மீ/வி என்ற சீரான வேகத்தில் செல்லுதல்
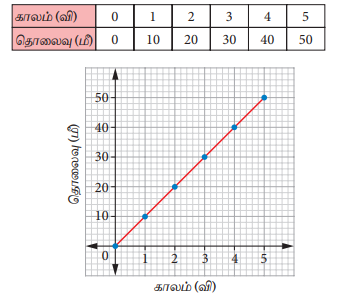
இந்த வரைபடத்தில் சாய்வின் மதிப்பு மாறாமல் உள்ளது. இதில் தொலைவானது ஒவ்வொரு விநாடியிலும் 10 மீட்டர் அதிகரிக்கிறது. எனவே, மகிழுந்து சீரான வேகத்தில் செல்கிறது.
(இ) மகிழுந்தின் வேகம் அதிகரித்துக் கொண்டே செல்லுதல்
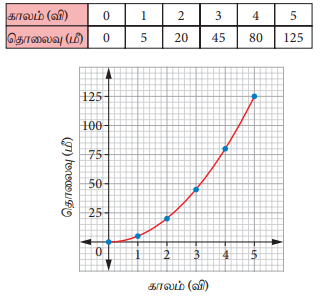
இந்த வரைபடத்தில் சாய்வின் மதிப்பு அதிகரித்துக் கொண்டே செல்கிறது. எனவே, மகிழுந்தின் வேகம் அதிகரித்துக் கொண்டே செல்கிறது.
(ஈ) மகிழுந்தின் வேகம் குறைந்து கொண்டே செல்லுதல்
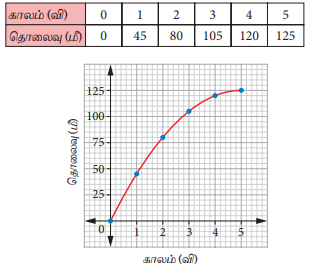
இந்த வரைப்படத்தில் சாய்வின் மதிப்பு அதிகரித்துக் கொண்டே செல்கிறது எனவே, மகிழுந்தின் வேகம் குறைந்துகொண்டே செல்கிறது.
வேகம் - காலம் வரைபடம்
ஒரு பேருந்தானது தஞ்சையிலிருந்து திருச்சியை நோக்கிச் செல்வதாகக் கருதுவோம். ஒவ்வொரு விநாடிக்கும் அதன் வேகமானது கணக்கிடப்படுகிறது. இதன் வேகம் மற்றும் காலத்தின் மதிப்புகள் அட்டவணைப்படுத்தப்பட்டு வரைபடமானது வரையப்படுகிறது. இவ்வரைப்படம் வேகம் - காலம் வரைப்படம் எனப்படுகிறது. இந்நிகழ்வில் காணப்படும் சாத்தியக்கூறுகள் கீழே கொடுக்கப்பட்டுள்ளன.
(அ) பேருந்து ஓய்வு நிலையில் இருத்தல்
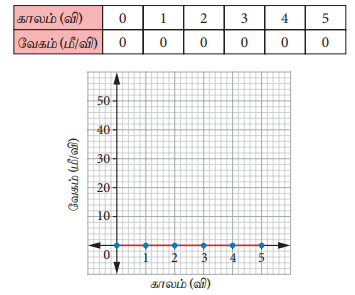
இங்கு வேகம் 0 மீ/வி என்ற நிலையிலேயே உள்ளது. எனவே, பேருந்து சுழி முடுக்கத்தினைக் கொண்டுள்ளது.
(ஆ) பேருந்து சீரான வேகத்தில் செல்லுதல்
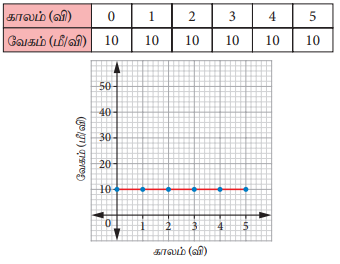
பேருந்து 10 மீ / வி என்ற மாறாத வேகத்தில் சென்று கொண்டிருக்கிறது. வரைபடத்தில், நேர்கோட்டின் சாய்வு சுழி மதிப்பைக் கொண்டுள்ளது. எனவே, இதன் முடுக்கம் சுழியாகும்.
(இ) பேருந்து சீரான முடுக்கத்தில் செல்லுதல்
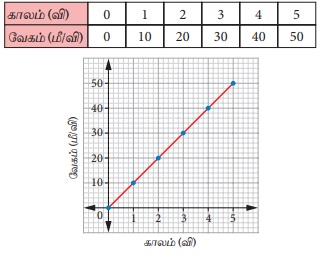
பேருந்தின் வேகம் ஒவ்வொரு விநாடியிலும் 10 மீ / வி என்று அதிகரித்து கொண்டே செல்கிறது. மேலும், வரைபடத்தில் நேர்கோட்டின் சாய்வானது நேர்குறியுடன் மாறாத மதிப்பைக் கொண்டுள்ளது. எனவே, இதன் முடுக்கம் மாறிலியாகும்.
(ஈ) பேருந்து சீரான எதிர் முடுக்கத்தில் செல்லுதல்
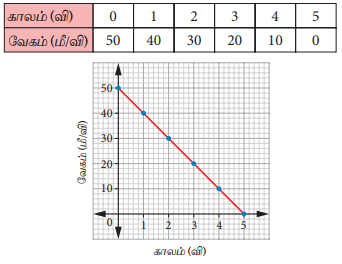
பேருந்தின் வேகம் ஒவ்வொரு விநாடியிலும் 10 மீ / வி என்ற குறைந்து கொண்டே செல்கிறது. வரைபடத்தில், நேர்கோட்டின் சாய்வானது எதிர்குறியுடன் மாறாத மதிப்பைக் கொண்டுள்ளது. எனவே, இதன் முடுக்கம் மாறிலியாகும். இந்த முடுக்கமானது எதிர்முடுக்கம் என அழைக்கப்படுகிறது.
(உ) பேருந்தின் முடுக்கம் அதிகரித்தல் (சீரற்ற முடுக்கம் )
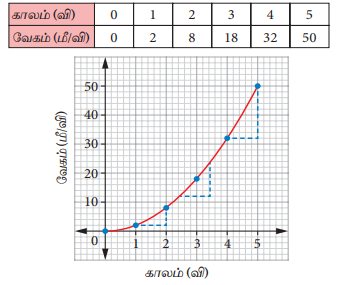
பேருந்தின் வேகமானது ஒவ்வொரு விநாடியிலும் அதிகரித்துக் கொண்டே செல்கிறது. இங்கு சாய்வானது நேர்குறி மதிப்பைக் கொண்டு, அதிகரித்துக் கொண்டே செல்கிறது. எனவே, இதன் முடுக்கம் அதிகரிக்கிறது.
(ஊ) பேருந்தின் முடுக்கம் குறைதல் (சீரற்ற முடுக்கம்)
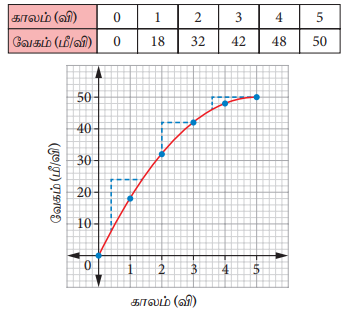
பேருந்தின் வேகமானது காலத்தினைப் பொருத்து குறைந்துகொண்டே செல்கிறது. மேலும், சாய்வானது நேர்குறி மதிப்பைக் கொண்டு, குறைந்துகொண்டே செல்கிறது. எனவே, இதன் முடுக்கத்தின் மதிப்பும் குறைந்து கொண்டே செல்கிறது.
தொலைவு - காலம் வரைபடம் மற்றும் வேகம் - காலம் வரைபடத்தை ஒப்பிடுதல்.

தொலைவு - காலம் வரைபடமும் வேகம் - காலம் வரைபடமும் ஒன்றுபோல் காணப்பட்டாலும் அவை பொருளின் பயணம் பற்றிய வெவ்வேறு தகவல்களை நமக்குப் அளிக்கின்றன. வரைபடம் மூலம் நாம் அவற்றை ஒப்பிடலாம்.