வாயு விதிகள்

வாயு விதிகள்

வேதியியலின் வளர்ச்சியில் வாயு விதிகள் முக்கிய பங்காற்றியுள்ளன. அழுத்தம், கன அளவு போன்ற பண்புகளை வெப்ப நிலையின் சார்புகளாக, அறிந்து கொண்டதன் மூலம் உருவாக்கப்பட்ட வாயு விதிகளின் அடிப்படையிலேயே வாயுக்களின் இயற்பண்புகள் அமைகின்றன. வாயு விதிகளைப்பற்றி விரிவாக கற்றறியும் முன்னர், முக்கிய காரணியான அழுத்தத்தினை பற்றி நாம் புரிந்து கொள்வோம்.

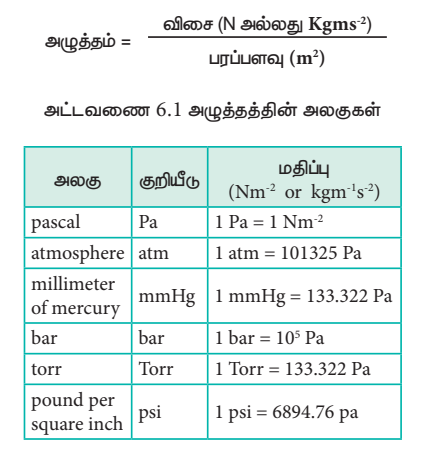
விசையினை, அவ்விசை செலுத்தப்படும் பரப்பினால் வகுக்கக் கிடைப்பது அழுத்தம் என வரையறுக்கப்படுகிறது. அழுத்தத்தின் SI அலகு பாஸ்கல் (Pascal) ஆகும். இதனை ஒரு சதுரமீட்டருக்கு ஒரு நியூட்டன் (Nm-2), என வரையறுக்கலாம். அழுத்தத்தினை குறிப்பிட மேலும் பல அலகுகள் நடைமுறையில் உள்ளன. அந்த அலகுகளுக்கும், SI அலகிற்கும் இடையேயான தொடர்பு பின்வருமாறு:

1. பாயில் விதி - (அழுத்தம் - கனஅளவு- தொடர்பு)

வாயுக்களின் அழுத்தம் மற்றும் கனஅளவு ஆகியவற்றிற்கு இடையேயான தொடர்பினை அறியும் பொருட்டு ராபர்ட் பாயில் தொடர்ச்சியான பரிசோதனைகளை மேற்கொண்டார். அவர் பயன்படுத்தியதைப் போன்ற மாதிரி உபகரண அமைப்பினை படம் (6.1)ல் காணலாம்.

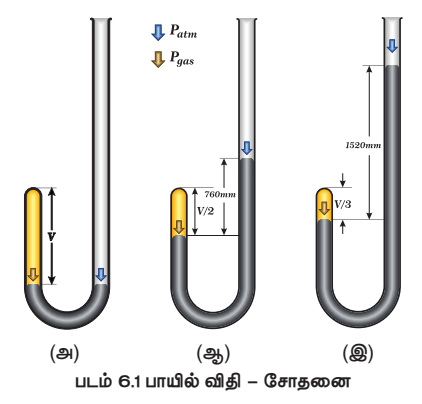
படம் 6.1 பாயில் விதி – சோதனை

படம் (61) ல் காட்டப்பட்டுள்ளவாறு, உபகரணத்தின் இரு முனைகளிலும் உள்ள பாதரச மட்டத்தின் அளவு சமமாகும் வகையில் உபகரணத்தின் திறந்த முனை வழியே பாதரசம் சேர்க்கப்படுகிறது.

மூடிய முனையில் அடைபட்டுள்ள காற்றின் கன அளவு, ஆரம்ப நிலையில் இருந்த அளவில் பாதியாகும். வகையில் கூடுதலாக பாதரசத்தினை சேர்க்கவும். இந்நிலை படம் 6.1 (ஆ) ல் காட்டப்பட்டுள்ளது. கூடுதலாக பாதரசம் சேர்க்கப்பட்டதால், வாயு உணரும் அழுத்தமானது. இரு முனைகளில் உள்ள பாதரச மட்டங்களுக்கு இடையேயான வேறுபாட்டினால் பெறப்படுகிறது. ஆரம்ப நிலையில் இரு முனைகளிலும் உள்ள பாதரச மட்டங்களுக்கு இடையே வேறுபாடு பூஜ்யமாகும். எனவே அடைபட்ட வாயு உணரும் அழுத்தம், வளிமண்டல அழுத்தமான 1 atm க்குச் சமம். அடைபட்ட வாயுவின் கனஅளவு ஆரம்ப அளவைக் காட்டிலும், சரிபாதியளவு குறைக்கப்படும் போது, பாதரச மட்டங்களுக்கு இடையேயான வேறுபாடு 760mm ஆக அதிகரிக்கிறது. இந்நிலையில் அடைபட்ட வாயு உணரும் அழுத்தம் 2 atm ஆகும். இதனடிப்படையில், ஒரு குறிப்பிட்ட வெப்பநிலையில், குறிப்பிட்ட நிறையுள்ள வாயு அடைத்துக் கொள்ளும் கனஅளவானது அதன் அழுத்தத்திற்கு எதிர்விகித தொடர்புடையது என பாயில் முடிவு செய்தார்.

கணிதவியல் முறைப்படி, பாயில் விதியினை கீழ்க்கண்டுள்ளவாறு எழுதலாம்

V α (1 / P) -------- (6.1)

( T மற்றும் n மாறிலிகள். T - வெப்பநிலை, n - மோல்களின் எண்ணிக்கை)

V = k × (1 / P) ---------- (6.2)

k - விகித மாறிலி

சமன்பாடு (6.2) ஐ நாம் மாற்றியமைக்கும் போது, மாறாத வெப்பநிலை மற்றும் நிறையில், 

PV = k ---------- (6.2a)

வாயுக்களின் வேதித்தன்மை எத்தகையதாக இருப்பினும், அனைத்து வாயுக்களுக்கும் அழுத்தம் குறைவாக உள்ள நிலையில் பாயில் விதி பொருந்தும்.

எனவே மாறாத வெப்பநிலையில், இருவேறு நிலைகளில் உள்ள குறிப்பிட்ட நிறையுள்ள ஒரு வாயுவிற்கு பாயில் விதியினை நாம் பின்வருமாறு எழுதலாம்

P1 V1 = P2 V2 = k ---------- (6.3)

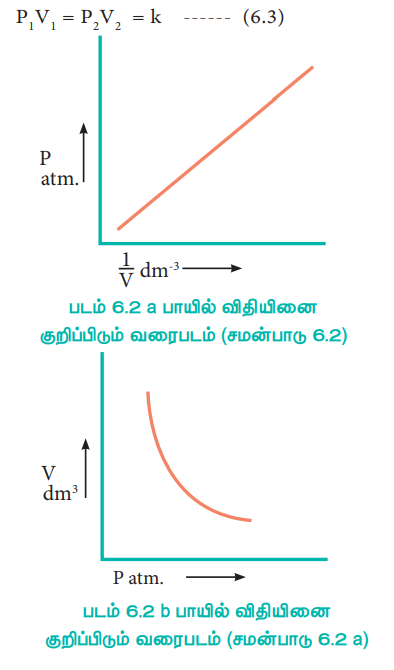
PV தொடர்பினை நாம் பின்வருமாறு புரிந்து கொள்ளலாம். வாயுக்களின் மூலக்கூறுகள் கொள்கலனின் சுவற்றின் மீது மோதுவதால் ஏற்படும் மூலக்கூறுகளின் மீதான விசை வாயுவின் அழுத்தத்திற்கு காரணமாக அமைகிறது. ஒரு குறிப்பிட்ட அளவுள்ள, வாயுவின் கன அளவு பாதியாகக் குறைக்கப்படும் போது, வாயுவின் அடர்த்தி இருமடங்காகிறது. எனவே, கலனின் ஓரலகு பரப்பில் மோதும் மூலக்கூறுகளின் எண்ணிக்கையும் இரு மடங்காகிறது. இதன் காரணமாக, வாயுவின் அழுத்தமும் இரு மடங்காக அதிகரிக்கிறது.

பாயில் விதியின் விளைவுகள்

பாயில் விதியிலிருந்து அழுத்தம் - அடர்த்தி இவற்றிற்கு இடையான தொடர்பினை பின்வருமாறு தருவிக்கலாம்.

P1 V1 = P2 V2 (பாயில் விதி)

P1 (m / d1) = P2 (m / d2)

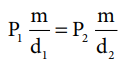
இங்கு “m” என்பது வாயுவின் நிறை, d1 மற்றும் d2 என்பன முறையே, P1 மற்றும் P2 அழுத்த நிலைகளில் அடர்த்தி மதிப்புகளைக் குறிப்பிடுகின்றன.

P1 / d1 = P2 / d2 ---------- (6.4)

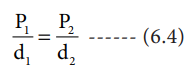
அதாவது, வாயுவின் அடர்த்தி, அதன் அழுத்தத்திற்கு நேர்விகித தொடர்புடையது.

உங்களுக்குத் தெரியுமா?

பயணிகள் விமானத்தின் உட்புறம் செயற்கையாக அழுத்த அதிகரிப்பு செய்யப்படுகிறது. ஏன் இவ்வாறு செய்யப்படுகிறது. என்பதை நீ அறிவாயா?

பெரும்பாலான ஆகாய விமானங்கள் சுமார் 30,000 அடி உயரத்தில் பறக்கும். உயரம் அதிகரிக்கும் போது ஓரலகு கன அளவில் காணப்படும் வாயு மூலக்கூறுகளின் எண்ணிக்கை குறைவாக இருப்பதால் அழுத்தம் குறையும். 

எனவே விமானம் காற்றில் உயரத்தில் செல்லும் போது அதனை சூழ்ந்துள்ள காற்றின் அழுத்தம் மிக குறைவாக  உள்ளதால், விமானத்தினுள் உள்ளவர் ஆக்சிஜன் குறைபாட்டிற்கு உள்ளாக வாய்ப்புள்ளது. இக்காரணத்தினால் தான் ஆகாய விமானங்களில் செயற்கையாக அழுத்த அதிகரிப்பு செய்யப்படுகிறது.

இதைப்போலவே, மலையேறும் ஒருவர், அழுத்தக் குறைவினால் ஏற்படும் விளைவினை, காதுகளில் ஏற்படும் சிறுவலியின் மூலம் உணரமுடியும். வெளிப்புற அழுத்தம் குறையும் போதிலும் காதின் உட்குழியில் உள்ள காற்றின் அழுத்தம் மாறாமல் இருக்கும். இது ஒரு சமநிலையற்ற நிலையினை ஏற்படுத்துகிறது. இந்த அதிகப்படியான உள் அழுத்தம், செவிப்பறையினை வெளிநோக்கி தள்ளுவதால் சிறு வலி ஏற்படுகிறது. சிறிது நேரத்தில் கொட்டாவி விடுவதால், செவி உட்குழியில் உள்ள மிகுதியான காற்று வெளியேறும் நிகழ்வின் காரணமாக உள் அழுத்தமும், வெளி அழுத்தமும் சமமாவதுடன், வலியினையும் குறைக்கிறது.

நீரில் மூழ்குபவர்கள், மூழ்கும் போது தேவையின்றி மூச்சினை அடக்கக் கூடாது என அறிவுரை வழங்கப்படுவதற்கு என்ன காரணம் என உங்களுக்குத் நெரியுமா?

படம் (6.3)ல் விடுபட்ட அளவீடுகளை (6.3 (b)ல் கனஅளவு மற்றும் 6.3 (c)ல் அழுத்தம்) கண்டறிவோம்.

தீர்வு:

பாயில் விதியின்படி, மாறாத வெப்பநிலையில், ஒரு குறிப்பிட்ட நிறையுடைய வாயுவிற்கு,

P1V1 = P2V2 = P3V3

1 atm × 1 dm3 = 2 atm × V2 = P3 × 0.25 dm3

ஃ 2 atm × V2 = 1 atm × 1 dm3

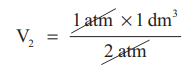
V2 = 0.5 dm3

and P3 × 0.25 dm3 = 1 atm × 1 dm3

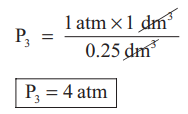
P3 = 4 atm 

தங்களை மதிப்பீடு செய்து கொள்ளுங்கள்

1. குளிர்சாதனப் பெட்டிகளில் குளிர்விப்பானாக பயன்படுத்தப்படும் ஃபிரியான்-12 சேர்மமானது, ஓசோன்படலம் சிதைவடைய காரணமாக அமைகிறது. தற்போது அதற்கு மாற்றாக சூழலுக்கு ஏற்ற சேர்மங்கள் பயன்படுத்தப்படுகின்றன. 0.3 atm அழுத்தம் மற்றும் 1.5 dm3 கனஅளவு உடைய ஃபிரியான் வாயு மாதிரியினைக் கருதுக. மாறாத வெப்பநிலையில், அழுத்தமானது 1.2 atmக்கு மாற்றப்படும் போது, அதிகரிக்கும் அல்லது குறையும் கனஅளவைக் கணக்கிடுக.

தீர்வு:

ப்ரீயானின் கனஅளவு (V1) = 1.5dm3

அழுத்தம் (P1) = 0.3 atm

T ஆனது மாறிலி P2 = 1.2 atm

V2 = ?

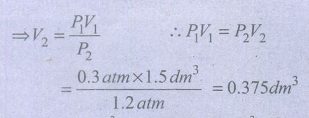
கனஅளவு 1.5dm3 லிருந்து 0.375 dm3 ஆகக் குறைகிறது.

2. ஒரு மோட்டார் வாகன இயந்திரத்தினுள் உள்ள உருளையில் (Cylinder) நிரம்பியுள்ள காற்றின் அழுத்தம் 1.05 atm ஆக உள்ள போது கனஅளவு 0.375 dm3, அதே வெப்பநிலையில் 0.125 dm3 க்கு அழுத்தப்படும்போது, அழுத்தப்பட்ட காற்றின் அழுத்தம் என்ன?

தீர்வு:

V1 = 0.375dm3

V2 = 0.125 dm3

P1 =1.05atm

P2 = ?

“T”மாறிலி

P1V1 = P2V2 

P2 = 3.15atm

2. சார்லஸ் விதி (கனஅளவு - வெப்பநிலை தொடர்பு)

J.A.C சார்லஸ் என்பவரால் வாயுவின் கனஅளவிற்கும், அதன் வெப்பநிலைக்கும் இடையேயான தொடர்பு குறித்து ஆய்வு மேற்கொள்ளப்பட்டது. ஒரு குறிப்பிட்ட நிறையுள்ள வாயுவிற்கு, அதன் அழுத்தம் மாறாதிருக்கும் போது, கன அளவானது அதன் வெப்பநிலையுடன் நேர்விகிதத் தொடர்புடையது என அவர் கண்டறிந்தார். இதனை கணித சமன்பாடாக பின்வருமாறு எழுதலாம் (P மற்றும் n மாறாதிருக்கும்போது)

V = kT -------- (6.5)

(அல்லது)

V / T =  மாறிலி

வாயுவில் வெப்பநிலை அதிகரிக்கும் போது V/T மாறிலியாக அமையும் வகையில் அதன் கனஅளவு நேர்விகிதத்தில் அதிகரிக்கிறது. மாறாத அழுத்தத்தில் உள்ள ஒரு அமைப்பிற்கு,

உதாரணமாக, பனிக்கட்டி குளிர் நிலையில் உள்ள நீரில் உள்ள ஒரு பலூனை, கொதி நீருள்ள மற்றொரு தொட்டிக்கு மாற்றும்போது, பலூனில் உள்ள வாயுவின் வெப்பநிலை அதிகரிக்கிறது. இதன் விளைவாக, பலூனிலுள்ள வாயு மூலக்கூறுகள் வேகமாக நகர்கின்றன. எனவே வாயு விரிவடைந்து, கனஅளவு அதிகரிக்கின்றது.

படம் 6.4. பனிக்கட்டி நீர் மற்றும் கொதி நீரில் காற்று நிரப்பப்பட்ட பலூன்

மாறாத அழுத்தத்தில், வெப்பநிலை, மாற்றத்தால், கனஅளவில் ஏற்படும் மாற்றம்.

ஒரு குறிப்பிட்ட அழுத்தத்தில், ஒரு வாயுவின் கனஅளவிற்கும், அதன் வெப்பநிலைக்கும் இடையேயான வரைபடம் 6.5ல் கொடுக்கப்பட்டுள்ளது. வரைபடத்திலிருந்து, குறிப்பிட்ட அழுத்தத்தில் வெப்பநிலை அதிகரிக்கும் போது வாயுவின் கனஅளவு நேர்விகிதத்தில் நேர்கோட்டில் அதிகரிக்கிறது என்பதை தெளிவாக அறிய முடிகிறது. இத்தகைய நேர்கோடுகள் ஐசோபார்கள் என்றழைக்கப்படுகின்றன. இதனை பின்வரும் நேர்கோட்டுச் சமன்பாட்டால் குறிப்பிடலாம்.

V = mT + C இங்கு T என்பது டிகிரி செல்சியஸில் வெப்பநிலை. m மற்றும் C ஆகியன மாறிலிகள்.

T = 0°C ஆக உள்ள போது கனஅளவு V0 ஆகிறது. எனவே, V0 = C மற்றும் நேர்கோட்டின் சாய்வு m = ΔV / ΔTக்குச் சமம். எனவே மேற்கண்டுள்ள சமன்பாட்டினை பின்வருமாறு எழுதலாம்.

V = (ΔV / ΔT) T + V0 ---------- (6.7)

மாறாத அழுத்தத்தில், சார்லஸ் மற்றும் கேலூசாக் ஆகிய அறிஞர்கள், ஒரு டிகிரி செல்சியஸ் வெப்பநிலை உயர்வினால், கனஅளவில் ஏற்படும் ஒப்பீட்டு அதிகரிப்பானது அனைத்து வாயுக்களுக்கும் ஒரேமாதிரியாக உள்ளன என கண்டறிந்தனர். ஒரு டிகிரி செல்சியஸ் வெப்பநிலை உயர்விற்கான கனஅளவில் ஏற்படும் ஒப்பீட்டு அதிகரிப்பு (α) என்பது (1 / V0) (ΔV / ΔT) க்குச் சமம்.

எனவே,

V / V0 = αT + 1

V = V0 (αT + 1) ---------- (6.9)

விரிவடைதல் குணகமானது தோராயமாக 1/273 என்ற மதிப்பிற்குச் சமம் என சார்லஸ் கண்டறிந்தார். அதாவது, மாறாத அழுத்தத்தில், ஒவ்வொரு டிகிரி வெப்பநிலை உயர்விற்கும், ஒரு குறிப்பிட்ட நிறையுள்ள, அனைத்து வாயுக்களும், 0°C ல் பெற்றுள்ள, அவைகளின் கன அளவைப் போல் 1/273 மடங்கு விரிவடைகின்றன.

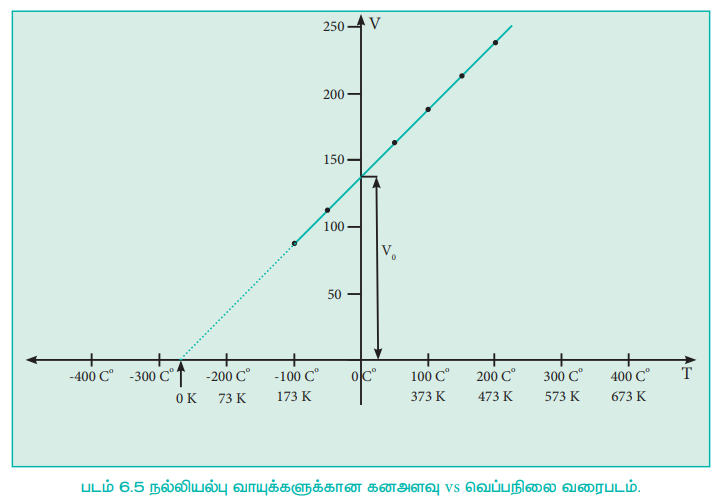
படம் 6.5 நல்லியல்பு வாயுக்களுக்கான கனஅளவு vs வெப்பநிலை வரைபடம்.

படம் 6.5ல் காட்டியுள்ளவாறு, சோதனை அளவீடுகளை விட குறைவான வெப்பநிலைகளுக்கு நேர்கோட்டினை நாம் நீட்டித்தால், அந்த நேர்கோடு x-அச்சினை -273°C ல் வெட்டுகிறது. இதிலிருந்து -273°C வெப்பநிலையில் (மிகத் துல்லியமாக -273.15°C ல்) வாயுவின் கனஅளவு பூஜ்ஜிய மதிப்பை பெறும், இவ்வெப்பநிலைக்குக் கீழ் வாயுவின் கனஅளவு எதிர்குறி மதிப்பினைப் பெற்றிருக்கவேண்டும். ஆனால் நடைமுறையில் இது சாத்தியமற்றதாகும். இதன் காரணமாக இந்த வெப்பநிலையை கெல்வின் தனிவெப்ப நிலை என வரையறுத்தார். மேலும் தனி பூஜ்ஜிய வெப்பநிலையை ஆரம்பப்புள்ளியாகக் கொண்டு, கெல்வின் புதிய வெப்பநிலை அளவுகோலினை உருவாக்கினார். தற்போது இந்த அளவுகோல் கெல்வின் அளவுகோல் என அழைக்கப்படுகிறது. கெல்வின் அளவுகோலின் பூஜ்யத்தின் நிலை மாற்றப்பட்டதே செல்சியஸ் வெப்பநிலை அளவுகோலுக்கும், கெல்வின் வெப்பநிலை அளவுகோலுக்கும் இடையே உள்ள ஒரே வேறுபாடாகும்.

எடுத்துக்காட்டு:

படம் (6.6)ல் விடுபட்ட அளவீடுகளை (6.6(b)ல் கனஅளவு 6.6(c)ல் வெப்பநிலை) நாம் கண்டறிவோம்.

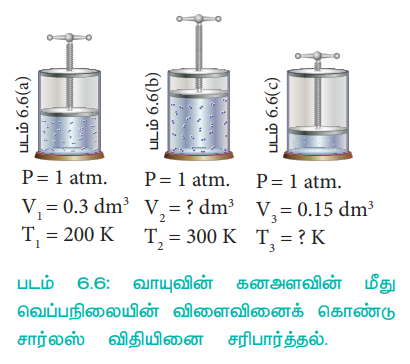
படம் 6.6: வாயுவின் கனஅளவின் மீது வெப்பநிலையின் விளைவினைக் கொண்டு சார்லஸ் விதியினை சரிபார்த்தல்,

தீர்வு:

சார்லஸ் விதிப்படி

T3 = 100 K

தன்மதிப்பீடு

3. ஒரு வாயு மாதிரியானது, ஒரு குறிப்பிட்ட வெப்பநிலையில் 3.8 dm3 கனஅளவினை பெற்றுள்ளது. இம்மாதிரியானது 0°Cல் உள்ள பனிகட்டி நீரில் அழுத்தப்படும்போது, அதன் கனஅளவு 2.27 dm3 ஆக குறைகிறது. அதன் ஆரம்ப வெப்பநிலை எவ்வளவு?

தீர்வு:

3. கேலூசாக்கின் விதி (அழுத்தம் வெப்பநிலை தொடர்பு)

மாறாத கனஅளவில், குறிப்பிட்ட நிறையுடைய வாயுவின் அழுத்தமானது அதன் வெப்பநிலையுடன் நேர்விகிதத் தொடர்புடையது என ஜோசப் கேலூசாக் கூறினார்.

P α T  

அல்லது

P / T = மாறிலி (K)

T1 மற்றும் T2 ஆகிய வெப்பநிலைகளில் வாயுவின் அழுத்த மதிப்புகள் முறையே P1 மற்றும் P2 எனில், கேலூசாக் விதிப்படி,

P1 / T1 = P2 / T2

செயல்பாடு - 1

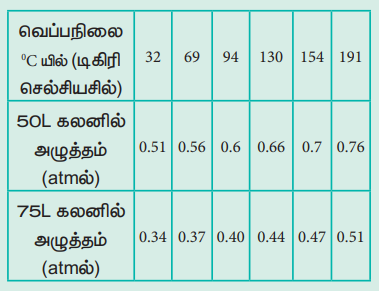
வெவ்வேறு வெப்பநிலைகளில், 1 மோல் நல்லியல்பு வாயுவின் அழுத்த மதிப்புகள், கீழ்க்கண்டுள்ள அட்டவணையில் கொடுக்கப்பட்டுள்ளது. இம் மதிப்புகளை வரைபடத்தில் குறிக்கவும் மற்றும் கேலூசாக் விதியினை சரிபார்க்கவும் (மாறா கனஅளவில்) ஒரு வாயுவின் அழுத்தம் Vs வெப்பநிலை வரைகோடுகள் சமகனஅளவு கோடுகள் (isochores) என அழைக்கப்படுகின்றன.

4. அவகேட்ரோ கருதுகோள்

சமவெப்பஅழுத்த நிலைகளில், சமகன அளவுள்ள அனைத்து வாயுக்களும், சம எண்ணிக்கையுள்ள மூலக்கூறுகளை பெற்றிருக்கும் என அவகேட்ரோ கருதினார். அவகேட்ரோ கருதுகோளை கணிதவியல் சமன்பாடாக பின்வருமாறு குறிப்பிடலாம்.

V α n,

V1 / n1 = V2 / n2 = மாறிலி ---------- (6.10)

இங்கு V1, n1 என்பன வாயுவின் கனஅளவு மற்றும் மோல்களின் எண்ணிக்கையினைக் குறிப்பிடுகின்றன. மற்றும் V2, n2 என்பன அதே வெப்ப அழுத்த நிலைகளில் வாயுவின் பிறிதொரு கனஅளவு மற்றும் மோல்களின் எண்ணிக்கையினைக் குறிப்பிடுகின்றன.

தன்மதிப்பீடு

4) ஒரு விளையாட்டு வீரரின் ஆழமான உட்சுவாசித்தலின் போது அவருடைய நுரையீரல் கனஅளவு 7.05 dm3 என மனித உடலியக்க ஆய்வு மூலம் (Kinesiology) கண்டறியப்பட்டுள்ளது. இக்குறிப்பிட்ட கனஅளவில் நுரையீரலானது 0.312 மோல்கள் காற்று மூலக்கூறுகளைக் கொண்டுள்ளது. வெளிச்சுவாசத்தின் போது நுரையீரலின் கனஅளவு 2.35 dm3 ஆக குறைகிறது. அவ்விளையாட்டு வீரர் வெளிசுவாசத்தின் போது வெளியேற்றும் காற்று மூலக்கூறுகளின் மோல்களின் எண்ணிக்கையினைக் கணக்கிடுக. (அழுத்தம் மற்றும் வெப்பநிலை மாறிலியாக இருப்பதாகக் கருதவும்)

தீர்வு:

V1 = 7.05 dm3 

V2 = 2.35dm3

ղ1 = 0.312mol

ղ2 = ?

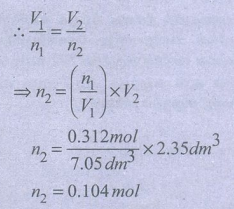
n2 = 0.104mol

வெளியிடப்படும் மோல்களின் எண்ணிக்கை

= 0.312  −  0.104 = 0.208 மோல்கள்