இயற்கணிதக் கோவைகளின் கூட்டல் மற்றும் கழித்தல்

இயற்கணிதக் கோவைகளின் கூட்டல் மற்றும் கழித்தல்

இயற்கணிதக் கோவைகள் குறித்துக் கற்றிருக்கிறோம். இப்போது இயற்கணிதக்கோவைகளைக் கூட்டவும் கழிக்கவும் காண்போம்.

சூழல்: கண்ணனிடம் சில முத்துக்கள் உள்ளன. கண்ணனிடம் உள்ளதைவிட 20 முத்துக்கள் அரவிந்தனிடம் அதிகமாக உள்ளன. கவிதா, இருவரிடமும் உள்ள முத்துக்களின் கூடுதலைவிட, மூன்று முத்துக்கள் தன்னிடம் அதிகமாக உள்ளது எனக் கூறினால், அவளிடமுள்ள மொத்த முத்துக்களின் எண்ணிக்கை எவ்வளவு?

இந்தச் சூழலில், மூவர் மூன்றுவிதமான எண்ணிக்கையில் முத்துக்களைக் கொண்டிருந்தாலும், அவை ஒன்றோடொன்று தொடர்பில் இருப்பதால், அவற்றை ஒரு மாறியாகவே கருதுவோம்.

கண்ணனிடம் உள்ள முத்துக்களின் எண்ணிக்கையை x என்க. அரவிந்தனிடம் கண்ணனைவிட 20 முத்துக்கள் அதிகம் உள்ளன. எனவே, x+20.

இருவரிடமும் உள்ளதைவிடவும் 3 முத்துக்கள் அதிகமாகக் கவிதாவிடம் உள்ளன. எனவே, கவிதாவிடம் உள்ள முத்துக்களின் எண்ணிக்கை x + x+20+3.

இப்போது, வேறு சூழலைக் கருதுவோம். கண்ணனிடம் உள்ளதைவிட 20 முத்துக்கள் அரவிந்தனிடம் குறைவாக உள்ளன என்று கருதுவோம். எனவே, அரவிந்தனிடம் உள்ள முத்துக்களின் எண்ணிக்கை x - 20 முத்துக்கள்.

இருவரிடமும் உள்ளதைவிடவும் 3 முத்துக்கள் அதிகமாகக் கவிதாவிடம் உள்ளன. எனவே, அவளிடம் உள்ள முத்துக்களின் எண்ணிக்கை x + x - 20 + 3.

எடுத்துக்காட்டாக 8ab, 4ab, 2ab ஆகியவற்றைக் (இங்கு ab என்பது மாறி) கூட்டுவதற்குக் கெழுக்களை மட்டும் கூட்டினால் போதுமானது.

அதாவது, 8ab + 4ab + 2ab = (8 + 4 + 2) ab = 14 ab = 14ab.

உறுப்புகளைக் கூட்டுவது போலவே, இயற்கணிதக் கோவைகளையும் கூட்ட முடியும். 11y + 7 மற்றும் 5y - 3 என்று கோவைகளைக் கருதுக. இங்கு 11y மற்றும் 5y என்பன y-ஐ மாறியாகக் கொண்ட ஒத்த உறுப்புகள், 7 மற்றும் - 3 என்பன மாறிலிகள் (ஒத்த உறுப்புகள்). 

எனவே , (11y + 7) + (5y - 3) = [11y + 5y] + [7 + ( - 3)]

= [(11 + 5) y] + (7 - 3)] 

= 16y + 4.

இவற்றை முயல்க

உறுப்புகளைக் கூட்டுக: 

i) 3p, 14p

3p + 14p = 17p

ii) m, 12m, 21m

m + 12m + 21m = 34m

iii) 11abc, 5abc

11 abc +5 abc =16 abc
iv) 12y, −y

12y + –y = 11y

v) 4x, 2x, − 7x

4x + 2x + – 7x

6x – 7x = –x 

எடுத்துக்காட்டு 3.5 

கோவைகளைக் கூட்டுக: 

(i) pq −1 மற்றும்  3pq + 2  

(ii) 8x + 3 மற்றும் 1 − 7x

தீர்வு  

(i) (pq − 1) + (3pq + 2) = (pq + 3pq) + ( − 1 + 2)

 = (1 + 3)pq + 1

= 4pq + 1

(ii) (8x + 3) + (1 − 7x) = 8x + 3 + 1 − 7x

 = (8x − 7x) + (3 + 1)

 = (8 − 7) x + 4

 = x + 4.

முழுக்களில் கற்றதைப் போலவே, இயற்கணிதக் கோவையின் உறுப்புகளைக் கழிப்பதும் அதன் கூட்டல் நேர்மாறைக் கூட்டுவதேயாகும். இயற்கணிதக் கோவைகளின் கழித்தலை நன்கு புரிந்துகொள்ள, ஓருறுப்பு இயற்கணிதக் கோவைகளின் கழித்தலைக் கருதுவோம்.

உதாரணமாக, 12y லிருந்து 6y ஐக் கழிக்க. நாம் 12y ஐயும், (- 6y) ஐயும் கூட்ட வேண்டும். ஆகவே, 12y + (-6y) = 12y – 6y

= (12 - 6)y = 6y. 

இதேபோல், 3mn லிருந்து -mn ஐக் கழிப்போம். -mn ன் கூட்டல் நேர்மாறு mn ஆகும். எனவே, 3mn ஐயும் mn ஐயும் கூட்டவேண்டும். அதாவது, 3mn + mn = (3 + 1)mn = 4mn.

இவ்வாறாக, இரு இயற்கணிதக் கோவைகளைக் கழிக்க முடியும். 25a + 11 என்னும் கோவையிலிருந்து 13a - 2 என்னும் கோவையைக் கழிக்க, 13a-2 இன் கூட்டல் நேர்மாறை 25a + 11 உடன் கூட்டவும்.

13a-2 இன் கூட்டல் நேர்மாறு -(13a-2) = -13a + 2. 

எனவே, 25a + 11 மற்றும் -(13a-2) ஐக் கூட்ட, 

எனவே, 25a + 11 - (13a - 2) = (25a + 11) + (-13a +2)

= (25a - 13a) + (11 + 2) 

= 12a + 13

குறிப்பு 

1.  4y என்பதைக் கழிப்பது என்பது – 4y ஐக் கூட்டுவதாகும். அதுபோல், - 11x ஐக் கழிப்பதுஎன்பது 11 x ஐக் கூட்டுவதாகும். 

2. -3 இன் கூட்டல் நேர்மாறு 3. அது போல, - x இன் கூட்டல் நேர்மாறு x. எனவே, x,-x  இன் எண்மதிப்புகள் சமமாகவும், ஆனால் எதிர்க்குறிகளுடனும் இருக்கும். 

எனவே, x+(-x) = 0.  ஆனால், x - (-x) = x+x = 2x ஆகும்.

எடுத்துக்காட்டு 3.6 

கழிக்க: i) 11pq லிருந்து 7pq

ii) a லிருந்து -a

iii) 21x + 9 லிருந்து 5x + 7

தீர்வு 

i)  7pq ன் கூட்டல் நேர்மாறு - 7pq

11pq + ( − 7pq) = 11pq − 7pq = (11 − 7)pq = 4pq 

ii) -a ன் கூட்டல் நேர்மாறு a.

ஆகவே, a + a = 2a 

iii)  21x + 9 – (5x + 7). 

(21x + 9) + [- (5x + 7)] = (21x + 9) - (5x + 7)

= 21x + 9 – 5x - 7 

= (21 - 5)x + (9 - 7) 

= 16x + 2.

சிந்திக்க

3x + (y − x) = 3x + y − x. ஆனால், 3x − (y − x) ≠ 3x − y − x.. ஏன்?

எடுத்துக்காட்டு 3.7 

சுருக்குக: 100x + 99y – 98z + 10x + 10y + 10z – x – y + z

தீர்வு 

கொடுக்கப்பட்ட இயற்கணிதக் கோவையில், x,y,z ஆகியன மாறிகள் ஒத்த உறுப்புகளைக் கண்டறிந்து தொகுத்து எழுதுவோம். 

100x + 99y - 98z + 10x + 10y + 10z - x - y + z

= (100x + 10x - x) + (99y + 10y - y) + ( -98z + 10z + z) 

= (100 + 10 - 1)x + (99 + 10 - 1)y + ( -98 + 10 + 1)z 

= (110 - 1)x + (109 - 1)y + ( -98 + 11)z 

= 109x + 108y + ( -87)z 

= 109x + 108y - 87z.

குறிப்பு 

இயற்கணிதக் கோவைகளைக் கூட்டவும் கழிக்கவும் அவற்றிலுள்ள ஒத்த உறுப்புகளை, அடைப்புக் குறிகளைப் பயன்படுத்தி, அடுத்தடுத்துக் கிடை வரிசையாக எழுதலாம்; அல்லது ஒன்றின் கீழ் ஒன்றாக செங்குத்து வரிசையிலும் எழுதலாம்.

எடுத்துக்காட்டு 3.8

i) கூட்டுக: 3x – 4y + z and 2x – z + 3y

ii) 4x + 3y லிருந்து, 2x - 5y -ஐக் கழிக்க. 

தீர்வு

i) (3x – 4y + z) + (2x – z + 3y)

= (3x + 2x) + ( -4y + 3y) + (z – z) 

= (3 + 2)x + ( -4 + 3)y + (1 - 1)z 

= 5x – 1y + 0z 

= 5x - y. 

மாற்றுமுறை :

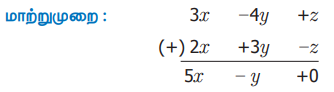
ii) (4x + 3y) - (2x – 5y)

= (4x + 3y) + ( -2x + 5y) 

= (4x – 2x) + (3y + 5y) 

= (4 - 2)x + (3 + 5)y 

= 2x + 8y.

மாற்றுமுறை :

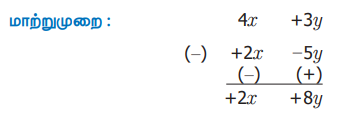
சிந்திக்க 

ஒரு எண்ணின் மூன்று மடங்கிலிருந்த அதன் இரண்டு மடங்கைக் கழித்தால் கிடைப்பது என்ன?

எடுத்துக்காட்டு 3.9

இரவு உணவு சாப்பிடுவதற்காக மணி தன் நண்பன் முகமது உடன் உணவகம் சென்றான். 2 இட்லிகளும், 2 தோசைகளும் மணி சாப்பிட்டான். முகமது 4 இட்லிகளும், 1 தோசையும் சாப்பிட்டான். x மற்றும் y முறையே, ஒரு இட்லியின் விலை மற்றும் ஓர் தோசையின் விலை எனில், அவர்கள் செலுத்தவேண்டிய பட்டியல் தொகையை (bill amount) x மற்றும் y இல் கணக்கிடுக.

தீர்வு 

ஓர் இட்லியின் விலை ‘x’ எனவும், ஒரு தோசையின் விலை y எனவும் கொடுக்கப்பட்டுள்ளது. 

எனவே, மணியின் பட்டியல் தொகை: (2 × x) + (2 × y) = (2x + 2y) 

முகமதுவின் பட்டியல் தொகை: (4 × x) + (1 × y) = 4x + y 

எனவே, மொத்தப் பட்டியல் தொகை = (2x + 2y) + (4x + y)

= (2 + 4)x + (2 + 1)y =6x + 3y. 

மாற்றுமுறை: 

மொத்தத்தில், அவர்கள் சாப்பிட்டவை 2 + 4 = 6 இட்லிகள்.

அதாவது 6 × x   = 6x

2 + 1 = 3 தோசைகள்

அதாவது 3 × y   = 3y 

எனவே, மொத்தப் பட்டியல் தொகை  = 6x + 3y.

எடுத்துக்காட்டு 3.10

ராணி வேலைக்குச் சென்ற முதல் நாள் ₹ 200 கூலியாகப் பெற்று, அதிலிருந்து ஒரு தொகையை அன்றே செலவு செய்தாள். மறுநாள் ₹ 300 கூலியாகப் பெற்று, அதிலிருந்து முதல்நாள் செலவழித்ததைப்போல், இருமடங்கு செலவு செய்தாள். மூன்றாம் நாள் ₹ 400 கூலியில், முதல் நாளைப்போல் 4 மடங்கு செலவு செய்தாள். இந்தச் சூழலிலிருந்து. அவளிடம் மூன்றாம் நாள் இறுதியில் மீதமிருக்கும் மொத்தத் தொகையைக் கணக்கிட உதவும் இயற்கணிதக் கோவையை உருவாக்குக.

தீர்வு 

முதல் நாள் பெற்ற கூலி ₹ 200. 

அன்று செலவிட்ட தொகையை ₹ x என்க. எனவே, முதல் நாள் மீதமிருக்கும் தொகை (200-x).

இரண்டாம் நாள் கூலி ₹ 300. அன்று செலவிட்ட தொகை ₹2x . இரண்டாம் நாள் மீதமிருக்கும் தொகை (300 – 2x). இதேபோல், மூன்றாம் நாள் மீதமிருக்கும் தொகை ₹ 400 – 4 x.

ஆகவே, மூன்றாம் நாள் இறுதியில் மொத்தமாக மீதமிருக்கும் தொகை (200-x) + (300 – 2x) + (400 – 4x). 

அதாவது, 200 + 300 + 400 + ( - 1- 2 - 4)x

= 900 + ( -7)x 

எனவே, 900 – 7 x என்பது தேவையான இயற்கணிதக் கோவையாகும்.

செயல்பாடு

இயற்கணிதத்தின் உதவியுடன் இந்த மாய எண் விளையாட்டை செயல்படுத்துக. 

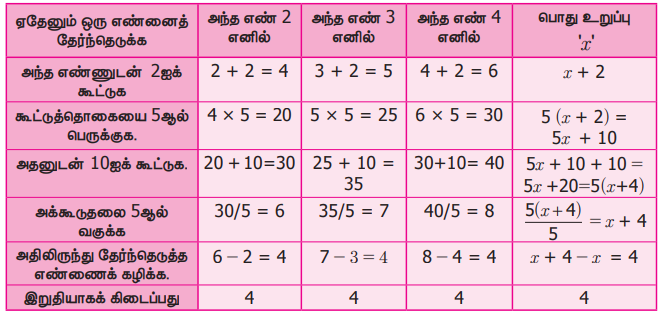
நாம் தேர்ந்தெடுக்கும் எண் எதுவாக இருந்தாலும், இறுதியாகக் கிடைக்கும் எண் 4 ஆகும். இதனை உன் நண்பர்களுடன் விளையாடி, அவர்களை ஆச்சரியப்படுத்தலாம். இயற்கணிதக் கோவைகளின் அடிப்படையில் இதன் வழிமுறை அட்டவணையின் இறுதி நிரலில் பொதுமைப்படுத்தப்பட்டுள்ளது. அதனை உற்றுநோக்குவதன் மூலம், புதிய எண் அமைப்புகளை உருவாக்கி விளையாட முயலலாம்