உறுப்புகள் மற்றும் அதன் கெழுக்கள்

உறுப்புகள் மற்றும் அதன் கெழுக்கள்

மாறிகளையும், மாறிலிகளையும், கூட்டல் மற்றும் கழித்தல் ஆகிய செயல்பாடுகள் மூலம் இணைத்து இயற்கணிதக் கோவைகள் உருவாக்கப்படுகின்றன.

உதாரணமாக, 6x + 1 என்னும் கோவை 6x, 1 என்னும் இரண்டு பகுதிகளின் கூடுதலினால் கிடைக்கப் பெறுகிறது. இந்தப் பகுதிகளே, ஒரு கோவையின் உறுப்புகள் எனப்படும். இங்கு 6x என்ற உறுப்பு மாறி உறுப்பு; 1 என்பது மாறிலி உறுப்பு. மேலும், 6, x என்பன 6x என்ற உறுப்பின் காரணிகளாகும்.

இதேபோல், 3ab + 5c என்ற கோவையில் 3ab, 5c ஆகியவை உறுப்புகளாகும். இங்கு, 3ab என்னும் உறுப்பின் காரணிகள் 3, a மற்றும் b ஆகும். இதேபோல் 5c என்ற உறுப்பின் காரணிகள் 5 மற்றும் c ஆகும்.

இயற்கணிதக் கோவைகள் குறித்து நன்கு புரிந்துகொள்ள, படம் 3.2 ஐக் கவனிக்கவும். கொடுக்கப்பட்டு உள்ள வடிவத்தின் சுற்றளவு எவ்வளவு?

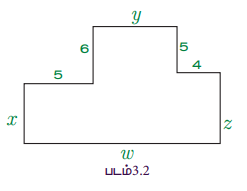
இதன் சுற்றளவு, 'P' = x + 5 + 6 + y + 5 + 4 + z + w அலகுகள்,

= x + y + z + w + (5 + 6 + 5 + 4)

= x + y + z + w + 20,

இங்கு x, y, z, w என்பன மாறிகள்; 20 ஒரு மாறிலி ஆகும்.

மேலே கொடுக்கப்பட்டுள்ள கோவையில் 5 உறுப்புகள் கூட்டலின் மூலம் இணைக்கப்பட்டுள்ளதைக் கவனிக்க.

6x - 5y + 3 என்னும் கோவையைக் கருதுக. இதன் உறுப்புகளைக் கண்டறிய 6x + (-5y)+3 என்று எழுதுவோம். இங்கு, 6x, (-5y), 3 ஆகியன உறுப்புகளாகும். எனவே, ஒரு கோவையில் ஒன்று, இரண்டு, மூன்றும் அதற்கும் மேற்பட்ட உறுப்புகள் இருக்கலாம்.

ஓர் இயற்கணிதக் கோவையின் உறுப்புகள் பின்வருவனவற்றுள் ஏதேனும் ஒன்றாக இருக்கலாம்:

சிந்திக்க 

ஓர் இயற்கணிதக் கோவையில்  உறுப்புகளை இணைப்பதற்குப் பெருக்கல் மற்றும் வகுத்தல் செயலிகளைப் பயன்படுத்த இயலுமா? 

i) மாறிலியாக (எடுத்துக்காட்டாக: 8, -11, 7, -1,...)

ii) மாறியாக (எடுத்துக்காட்டாக: x,a,p,y,…….)

iii) இரண்டு அல்லது அதற்கு மேற்பட்ட மாறிகளின் பெருக்கற்பலன் (எடுத்துக்காட்டாக: xy, pq, abc,...) 

iv) மாறிலி மற்றும் மாறியின் பெருக்கற்பலனாக (எடுத்துக்காட்டாக: 5x, -7pq, 3abc,…….. )

குறிப்பு 

ஓர் இயற்கணிதக் கோவையில் ஒன்று, இரண்டு அல்லது அதற்கு மேற்பட்ட உறுப்புகள் இருக்கலாம். ஓர் உறுப்பு மட்டும் உள்ள கோவை 'ஓருறுப்புக் கோவை' என்றும், இரண்டு உறுப்புகள் உள்ள கோவை ‘ஈருறுப்புக் கோவை' என்றும், மூன்று உறுப்புகள் உள்ள கோவை 'மூவுறுப்புக் கோவை’ என்றும் அழைக்கப்படுகின்றன. ஒன்று அல்லது அதற்கு மேற்பட்ட உறுப்புகள் கொண்ட கோவை ‘பல்லுறுப்புக் கோவை' எனப்படும். உதாரணமாக, 2x என்னும் கோவை ஓருறுப்புக் கோவை;2x + 3y என்பது ஈருறுப்புக் கோவை; 2x + 3y + 4z என்பது மூவுறுப்புக் கோவையாகும். இவையனைத்தும் பல்லுறுப்புக் கோவைகளாகும்.

செயல்பாடு  

மாறியையும், மாறிலியையும் நன்கு புரிந்துகொள்ளப் பின்வரும் செயல்பாட்டினை மேற்கொள்வோம்.

அட்டைகளை உடைய இரு கூடைகளைக் கருதுவோம். ஒன்றில் மாறிலியும், மற்றொன்றில் மாறியும் உள்ளன. முதல் கூடையில் இருந்து ஒரு மாறியையும், இரண்டாம் கூடையில் இருந்து ஒரு மாறிலியையும் எடுத்து, அவ்விரண்டின் பெருக்கற்பலனாக ஓர் உறுப்பை உருவாக்க வேண்டும்.

மாதிரிக்கு இரண்டு பெட்டிகள் நிரப்பப்பட்டுள்ளன. இதேபோல், அனைத்து உறுப்புகளையும் கண்டறிந்து அட்டவணையை நிறைவு செய்க. 

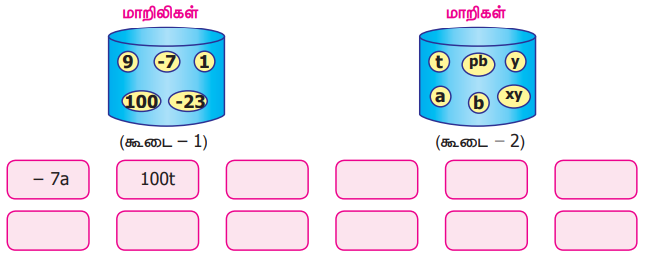
விடைகள் :  

இவற்றை முயல்க 

கொடுக்கப்பட்ட உறுப்புகளைப் பயன்படுத்தி இயற்கணிதக் கோவைகளை உருவாக்கிப் பின்வரும் அட்டவணையை நிரப்புக. மாதிரிக்காக ஒன்று செய்து காண்பிக்கப்பட்டுள்ளது. 

எடுத்துக்காட்டு 3.1 

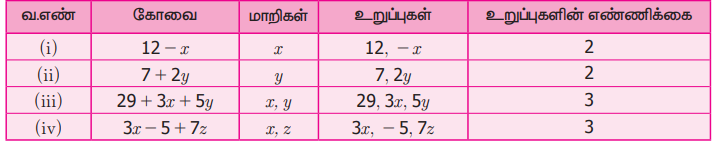
பின்வரும் கோவைகளில் மாறி, உறுப்புகள் மற்றும் உறுப்புகளின் எண்ணிக்கையைக் காண்க 

(i) 12 − x 

(ii) 7 + 2y 

(iii) 29+3x+5y (iv) 3x–5+7z 

தீர்வு 

1. உறுப்பின் கெழு

ஓர் இயற்கணிதக் கோவையின், ஓர் உறுப்பு என்பது அதன் காரணிகளின் பெருக்கற்பலனாகும். இங்கு ஒவ்வொரு காரணிக்கும் அல்லது காரணிகளின் பெருக்கற்பலனுக்கும் மீதமுள்ள காரணிகளின் பெருக்கல் அதன் கெழு என்று அழைக்கப்படும்.

உதாரணமாக, 5xy என்னும் உறுப்பில், 5 என்பது மீதமுள்ள காரணிகளான பெருக்கல் xy க்கு கெழுவாகும். இதேபோல், x என்பது 5y இன் கெழு; 5x என்பது y இன் கெழு. 5 எனும் மாறிலியை எண்கெழு எனவும், மற்றவற்றைக் கெழு எனவும் குறிப்பிடுவோம்.

எனவே, கெழு என்பது எண் காரணியாகவோ, அல்லது இயற்கணிதக் காரணியாகவோ அல்லது இரண்டின் பெருக்கலாகவோ இருக்கும். பொதுவாக, ஓர் உறுப்பின் கெழு என்பது அதன் எண்கெழுவைக் குறிக்கும். ஓர் உறுப்பில் எண் காரணிகள் இல்லாதபோது, அதன் எண்கெழு 1 எனக் கருதப்படும்.

– 6ab என்னும் உறுப்பைக் கருதுக. இவ்வுறுப்பு – 6, a மற்றும் b ஆகிய மூன்று காரணிகளின் பெருக்கற்பலனாகும். மேலும், இதனை இரு காரணிகளின் பெருக்கலாகப் பின்வருமாறு எழுதலாம்: 

-6a × b,  -6b × a மற்றும் – 6 × ab.

‘a’ இன் கெழு – 6b 

‘b' இன் கெழு - 6a

‘ab' இன் கெழு - 6 

இங்கு – 6 என்பது -6ab என்னும் உறுப்பின் எண்கெழு ஆகும். 

எடுத்துக்காட்டு 3.2 

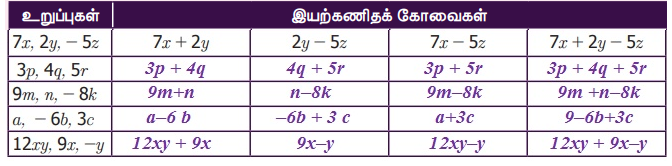
பின்வரும் உறுப்புகளின் எண்கெழுக்களைச் காண்க. மேலும், ஒவ்வொரு உறுப்பிற்கும் x மற்றும் y இன் கெழுக்களைக் காண்க: 3x, −5xy, −yz, 7xyz, y, 16yx. 

தீர்வு