பயிற்சி : 3.4

பயிற்சி : 3.4

பலவகைத் திறனறி பயிற்சிக் கணக்குகள் 

1. 3ab + 8 லிருந்து -3ab - 8 ஐக் கழிக்க. மேலும் -3ab - 8 லி இருந்து 3ab + 8 ஐக் கழிக்க.

தீர்வு : 

i) (3ab + 8) - (-3ab - 8)

= 3ab + 8 + 3ab + 8 

= 6ab + 16

ii) (-3ab - 8) - (3ab + 8) 

= -3ab - 8 - 3ab - 8 

= -6ab - 16

2. x + 3y, 2x + y, x - y ஆகியனவற்றைப் பக்கங்களாகக் கொண்ட முக்கோணத்தின் சுற்றளவு காண்க.

தீர்வு : 

முக்கோணத்தின் சுற்றளவு = பக்கங்களின் கூடுதல் 

= (x + 3y) + (2x + y) + (x - y) 

= x + 3y + 2x + y + x - y 

= 4x + 3y

3. ஓர் எண்ணின் மூன்று மடங்குடன் 5 ஐக் கூட்ட 44 கிடைக்கிறது. அந்த எண்ணைக் காண்க. 

தீர்வு :

அந்த எண் x என்க 

3x + 5 = 44 

3x = 44 - 5 = 39 

3x = 39

x = 39 / 3 ⇒ x = 13

அந்த எண் 13.

4. 5ab - 3ab + 2c ஐ விட 2ab + 4b - c எவ்வளவு சிறிய கோவை? 

தீர்வு : 

(5ab - 3b + 2c) - (2ab + 4b - c)

= 5ab - 3b + 2c - 2ab - 4b + c

= 3ab - 7b + 3c 

5. ஓர் எண்ணின் ஆறு மடங்கை 40 லிருந்து கழித்தால் '-8' கிடைக்குமெனில், அந்த எண்ணைக் காண்க. 

தீர்வு : 

அந்த எண் x என்க

40 - 6x = -8 

40 + 8 = 6x 

6x = 48

x = 48 / 6

ஃ அந்த எண் 8

மேற்சிந்தனைக் கணக்குகள்

6. 5x + 7y - 12 மற்றும் 3x - 5y + 2, ஆகியவற்றின் கூடுதலில் இருந்து, 2x - 7y - 1 மற்றும் -6x + 3y + 9 ஆகியவற்றின் கூடுதலைக் கழிக்க. 

தீர்வு :  

i) (5x + 7y - 12) + (3x - 5y + 2)  

= 5x + 5x + 7y - 5y - 12 + 2

= 8x + 2y - 10 ------- (1) 

ii) (2x - 7y - 1) + (-6x + 3y + 9) 

= 2x - 6x - 7y + 3y – 1 + 9

= -4x - 4y + 8 ------- (2)

(1) - (2) = (8x + 2y - 10) - (-4x - 4y + 8)

= 8x + 2y - 10 +  +4x + 4y - 8

= 12x + 6y - 8 

7. 5a - 3b + 2C உடன் எந்தக் கோவையைக் கூட்டினால் a - 4b - 2c கிடைக்கும்? 

தீர்வு : 

அந்த கோவையை x என்க

x + (5a - 3b + 2c) = a - 4b - 2c 

x = a - 4b - 2c - 5a + 3b - 2c 

x = -4a – b - 4c

ஃ அந்த கோவை -4a – b - 4c ஆகும். 

8. 2m + 8n + 10 லிருந்து, எதனைக் கழித்தால் -3m +7n + 16 கிடைக்கும்? 

தீர்வு : 

அந்த கோவையை x என்க 

(2m + 8n + 10) - x = -3m + 7n + 16

 (2m + 8n + 10) - (-3m + 7n + 16) = x

x = 2m + 8n + 10 + 3m - 7n - 16

x = 5m + n - 6 

ஃ அந்த கோவை 5m + n - 6 ஆகும். 

9. பின்வரும் கூற்றுக்குப் பொருத்தமான, இயற்கணிதச் சமன்பாட்டைத் தருக: "ஒரு செவ்வகத்தின் பரப்பளவுக்கும் சுற்றளவுக்கும் இடைப்பட்ட வித்தியாசம் 20" 

தீர்வு : 

பரப்பு = lb ச.அ, சுற்றளவு= 2 (l + b) 

சமன்பாடு lb - [ 2 (l + b) ] = 20 

lb - 2 (l + b) = 20

10. கூட்டுக : 2a + b + 3c, a + 1/3 b + 2/5 c

தீர்வு : 

(2a + b + 3c) + (a + 1/3 b + 2/5 c)

= 2a + a + b + b/3 + 3c + 2c/5

= 3a + (3b + b) / 3 + (15c + 2c) / 5

= 3a + 4b / 3 + 17c / 5

கணிதப் புதிர்களே இயற்கணிதம் என்னும் கணிதப் பிரிவுக்குத் தோற்றுவாயாக இருக்கின்றன. 12ஆம் நூற்றாண்டில், மஹாராஷ்டிராவில் வாழ்ந்த பாஸ்கராச்சார்யா (பாஸ்கரா II) என்னும் கணிதமேதை இயற்றிய ‘லீலாவதி’ என்னும் நூலே, இந்தியாவின் முதல் கணிதப் புதிர் நூலாகும். அந்த நூலில் இருந்து ஓர் ஆர்வமூட்டும் புதிர் கணக்கு, இதோ உங்களுக்காக  

“ஒரு முத்துமாலை அறுந்து, முத்துக்கள் சிதறி விழுந்தன. முத்துக்களில் மூன்றில் ஒரு பங்கு தரையில் விழுந்தது. ஐந்தில் ஒரு பங்கு கட்டிலுக்கு அடியில் உருண்டோடியது. இருவர் அந்த முத்துக்களைச் சேகரிக்க ஆரம்பித்தனர் ஒருவர் ஆறில் ஒரு பங்கும், மற்றொருவர் பத்தில் ஒரு பங்குமாக முத்துக்களைக் கைகளில் சேகரித்தனர். முத்து மாலையில் 6 முத்துக்கள் மட்டுமே மீதமிருந்தால், அந்த மாலையில் இருந்த மொத்த முத்துக்கள் எத்தனை?"

தீர்வு : 

மொத்த முத்துக்களின் எண்ணிக்கை 'x' என்க.

கொடுக்கப்பட்ட விவரங்களிலிருந்து, நாம் பின்வரும் இயற்கணிதச் சமன்பாட்டை உருவாக்கலாம்.

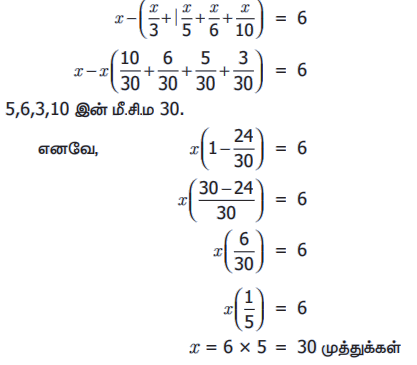
x = 6 × 5 = 30 முத்துக்கள்

விடைகள் 

பயிற்சி -3.4

1. 6 ab + 16; − 6ab − 16

2. 4 x + 3y

3. x = 13

4. 3ab − 7b + 3c

5. x = 8

 மேற்சிந்தனைக் கணக்குகள்

6. 12x + 6 y − 18

7. −4a − b − 4c

8. 5m + n − 6

9. lb − 2 ( l + b) = 20

10. 3a + 4/3 b + 17/5 c