இயற்கணிதம் | முதல் பருவம் அலகு 3 | 7ஆம் வகுப்பு கணக்கு - எளிய நேரிய சமன்பாடுகள் | 7th Maths : Term 1 Unit 3 : Algebra
7ஆம் வகுப்பு கணக்கு : முதல் பருவம் அலகு 3 : இயற்கணிதம்
எளிய நேரிய சமன்பாடுகள்
எளிய நேரிய சமன்பாடுகள்
எளிய நேரிய சமன்பாடுகளை உருவாக்கவும் அவற்றைத் தீர்க்கவும் கற்போம்.
1. நேரிய சமன்பாடுகளை உருவாக்குதல்
7x + 3 என்னும் கோவையைக் கருதுக. இங்கு 'x' மாறி ஆகும்.
x= 2, எனும்போது, கோவையின் மதிப்பு (7 × 2) + 3 = 14 + 3 = 17 ஆகும்.
x = 2 என்னும் போது இதனை, 7x + 3 = 17 என எழுதலாம். இங்கு, 7x + 3 = 17 என்பது சமன்பாடு எனப்படும்.
மேற்கூறிய உதாரணத்தில், x = 2 என்பது கட்டுப்பாட்டை நிறைவு செய்கிறது. மேலும் 2-ஐத் தவிர x இன் வேறெந்த மதிப்பிற்கும் 7x + 3 = 17 என்னும் கட்டுப்பாடு நிறைவடையவில்லை . எனவே, x = 2 என்பது 7x + 3 = 17 என்னும் சமன்பாட்டின் தீர்வு என்று அழைக்கப்படும்.
ஒரு சமன்பாடானது, ஒரு எண் மதிப்பிற்கோ அல்லது வேறொரு இயற்கணிதக் கோவைக்கோ சமமாகவே எப்போதும் இருக்கும். சமக்குறியானது, ‘=' குறிக்கு இடதுபுறமுள்ள கோவையின் மதிப்பும், '=' குறியின் வலதுபுறமுள்ள கோவையின் மதிப்பும் சமம் என்பதைக் குறிக்கிறது.
பொதுவாக வலதுபுறம் ஓர் எண்தான் இருக்கும். ஆனால், எப்போதும் அப்படி இருக்கவேண்டிய அவசியமில்லை. வலதுபுறம், மாறியுடன் கூடிய கோவையும் இருக்கலாம். உதாரணமாக, 7x + 3 = 3x-1 என்னும் சமன்பாட்டில், சமக்குறிக்கு இடதுபுறம் (L.H.S) என்னும் கோவையும், வலதுபுறம் (R.H.S) 3x-1 என்னும் கோவையும் உள்ளது.
மாறியின் மதிப்பறியாத நிலையில், அதன் கோவையின் மதிப்பு அறிந்த சில சூழல்களைப் பார்ப்போம்.
10 நாற்காலிகள், 4 மேஜைகள் ஆகியவற்றின் விலை ₹ 4000 என்க. இங்கு ஒரு நாற்காலி அல்லது ஒரு மேஜையின் விலை கொடுக்கப்படவில்லை ஒரு நாற்காலியின் விலை ₹ x மற்றும் ஒரு மேஜையின் விலை ₹ y என்க. எனவே, 10 நாற்காலிகள், 4 மேஜைகள் ஆகியவற்றின் விலை ₹ 10x + 4y ஆகும். எனவே, 10x+4y=4000 ஆகும். இது 4000 எண் மதிப்பைப் பெற்ற x, y ஆகிய இரு மாறிகளில் அமைந்த சமன்பாடாகும்.
பின்வரும் கூற்றுகளுக்குப் பொருத்தமான இயற்கணிதச் சமன்பாடுகளை உருவாக்குவோம்.
1. "ஓர் ஆப்பிள் மற்றும் இரு மாம்பழங்களின் விலை ₹ 120"
ஆப்பிளின் விலை a எனவும், மாம்பழத்தின் விலை m எனவும் கருதினால், தேவையான சமன்பாடு a + 2m = 120.

2. "ஒரு செவ்வகத்தின் சுற்றளவு 50 செ.மீ".
செவ்வகத்தின் நீளம் மற்றும் அகலத்தை 'l' மற்றும் 'b' என்று கருதினால், 2 (l + b) = 50 என எழுதலாம்.
3. "தாமரையின் வயது அவள் தங்கை செல்வியை விட 4 வயது அதிகம். மேலும் இருவரின் வயதுகளின் கூடுதல் 24".
தாமரை மற்றும் செல்வியின் வயதுகளை மாறிகளாகக் கருதுவோம். அவர்களின் வயது வெவ்வேறாக இருந்தபோதும், அவற்றை ஒரே மாறியாகக் கருதுவோம். ஏனெனில், தாமரையின் வயது, செல்வியின் வயதுடன் தொடர்புபடுத்தப்பட்டுள்ளது.
ஒருவேளை செல்வியின் வயது 10 ஆக இருக்குமெனில், தாமரையின் வயது 10 + 4 = 14 ஆகும். அவ்வாறாக, செல்வியின் வயது x எனில், தாமரையின் வயது x + 4 ஆகும்.
ஆகவே, x + (x + 4) = 24. என்ற சமன்பாடு கிடைக்கிறது. அதாவது, 2x + 4 = 24
ஆகவே, ஒரு சமன்பாடு எனப்படுவது, ஒரு மாறிலிக்கோ அல்லது மற்றொரு இயற்கணிதக் கோவைக்கோ சமப்படுத்தப்பட்ட, ஓர் இயற்கணிதக் கோவையாகும்.
இவற்றை முயல்க
பின்வரும் வாய்மொழிக் கூற்றுகளுக்குப் பொருத்தமான இயற்கணிதச் சமன்பாடுகளை உருவாக்குக.
1. ஓர் எண்ணின் மூன்றில் ஒரு பங்குடன் 6ஐக் கூட்டக் கிடைப்பது 10.
1/3 x + 6 = 10
2. x ன் ஐந்து மடங்குடன் 3ஐக் கூட்டக் கிடைப்பது 28.
5x + 3 = 28
3. y லிருந்து 8 ஐக் குறைத்தால் 11 கிடைக்கிறது.
y – 8 = 11
4. பக்கம் a உடைய ஒரு சதுரத்தின் சுற்றளவு 16 செ.மீ.
4a =16
5. வெங்கட்டின் அம்மாவின் வயது வெங்கட் வயதின் 3 மடங்குடன் 7ஐக் கூட்டக் கிடைப்பது ஆகும். அவனுடைய அம்மாவின் வயது 43 ஆகும்.
2. சமன்பாட்டைத் தீர்த்தல்
ஒரு சமன்பாடு என்பது எடைத் தராசு போன்றது. தராசின் இரு தட்டுகளிலும் சம எடை இருக்கும்போது, அதன் முள் நேராக இருக்கும். இருபுறமும் சம எடையை அதிகரிக்கும் போதும், குறைக்கும்போதும் அதன் முள் எந்தப் பக்கமும் சாயாமல், நேராகவே இருக்கும்.
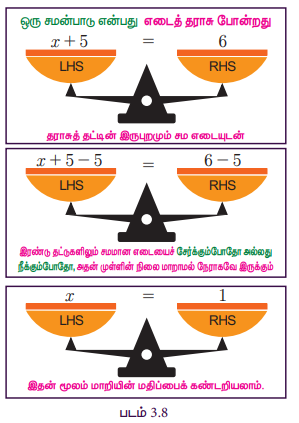
இந்தக் கொள்கை இயற்கணிதச் சமன்பாடுகளைத் தீர்ப்பதற்கும் பொருந்தும். ஒரு சமன்பாட்டைத் தீர்ப்பதற்குப் பின்வரும் வழிமுறைகளைப் பயன்படுத்தி அதன் மாறிகளையும், மாறிலிகளையும் தனித்தனியே பிரிக்கின்றோம்.
1. ஒரு சமன்பாட்டின் இருபுறமும் ஒரே எண்ணைக் கூட்டுவதாலோ அல்லது கழிப்பதாலோ, அதன் சமத்தன்மை மாறாது. உதாரணமாக, x + 5 = 12 என்னும் சமன்பாட்டைத் தீர்க்க, இருபுறமும் 5 ஆல் கழிக்க வேண்டும். அதாவது, x + 5 - 5 = 12 - 5.
x + 0 = 7 எனவே x = 7 [ஏனெனில், 0 என்பது கூட்டல் சமனி]
சிந்திக்க
ஏன் 5ஐக் கழிக்கவேண்டும்? ஏன் வேறு எண்ணைக் கழிக்கக்கூடாது? 5 ஐ இருபுறமும் கூட்டினால் என்னவாகும் என்று விவாதிக்க
2. இதேபோல், ஒரு சமன்பாட்டின் இருபுறம் ஒரே எண்ணைப் பெருக்குவதாலோ அல்லது வகுப்பதாலோ அதன் சமநிலை மாறாது. உதாரணமாக, 5y = 20 எனும் சமன்பாட்டைத் தீர்க்க, இருபுறமும் 5ஆல் வகுக்க வேண்டும்.
அதாவது 1/5 × = 5y = 20 / 5 . எனவே y = 4
3. சமன்பாட்டின் இருபுறமுள்ள கோவைகளை இடமாற்றம் செய்வதால், அதன் சமநிலை மாறாது. அதாவது, 7x + 3 = 17 என்பதும் 17 = 7x + 3 என்பதும் ஒரே சமன்பாடுதான். அதேபோல், 7x + 3 = 3x – 1 என்பதும் 3x -1 = 7x + 3 என்பதும் ஒன்றேயாகும்.
இவற்றை முயல்க

நாய், பூனை, கிளி ஆகியவை மாறிகளைக் குறிக்குமெனில், அவற்றைக் காண்க. கிடைத்த மதிப்புகளைச் சமன்பாடுகளில் பிரதியிட்டுச் சரிபார்க்க.
8 + 8 + 8 = 24
8 + 3 + 3 = 14
8 + 3 – 2 = 9
8 + 3 + 2 = 13
எடுத்துக்காட்டு 3.11
அடுத்தடுத்த இரு இயல் எண்களின் கூடுதல் 75 எனில், அவ்விரு எண்களைக் காண்க.
தீர்வு
அந்த எண்களை x மற்றும் x + 1 என்க.
x + (x + 1) = 75 (கொடுக்கப்பட்டது)
2x+ 1 = 75
2x + 1 - 1 = 75 - 1 (இருபுறமும் 1ஐக் கழிக்க)
2x + 0 = 74
2x / 2 = 2x / 2 (இருபுறமும் 2ஆல் வகுக்க)
x = 37; x + 1 = 38
எனவே, தேவையான எண்கள் 37 மற்றும் 38 ஆகும்.
எடுத்துக்காட்டு 3.12
ஒருவர் ₹960 இக்கு ₹1, ₹5 மற்றும் ₹10 ஆகிய மதிப்பிலான பணத் தாள்களை வைத்துள்ளார். இம்மூன்று மதிப்பிலுள்ள பணத்தாள்களின் எண்ணிக்கையும் சமமெனில், அவரிடமுள்ள மொத்தப் பணத்தாள்களின் எண்ணிக்கை எவ்வளவு?
தீர்வு
ஒவ்வொரு மதிப்பிலும் உள்ள பணத்தாள்களின் எண்ணிக்கை x என்க.
ஆகவே, x + 5 x + 10 x = 960
(1 + 5 + 10) x = 960
16 x = 960
இருபுறமும் 16ஆல் வகுக்க,
16 x /16 = 960/16 = 60
எனவே, x = 60
எனவே, ஒவ்வொரு மதிப்பிலுமான பணத்தாள்களின் எண்ணிக்கை 60.
எடுத்துக்காட்டு 3.13
ஒரு தேர்வில், மாணவர் எழுதும் சரியான விடைக்கு 4 மதிப்பெண்கள் வழங்கப்படுகின்றன. மேலும், தவறான விடைக்கு 1 மதிப்பெண் குறைக்கப்படுகிறது. அத்தேர்வில், ஒருவன் மொத்தம் 60 வினாக்களுக்கு விடை எழுதி 130 மதிப்பெண்கள் பெற்றான் எனில், சரியான விடை எழுதிய வினாக்களின் எண்ணிக்கை எவ்வளவு?
தீர்வு
சரியான விடை எழுதிய வினாக்களின் எண்ணிக்கை x என்க
எனவே தவறான விடை எழுதிய வினாக்கள் = 60 - x
ஆகவே, 4x - 1 (60 - x) = 130
4 x - 60 + x = 130
4x + x - 60 + 60 = 130 + 60 (இருபுறமும் 60ஐக் கூட்ட)
5 x + 0 = 190
5 x = 190
இருபுறமும் 5ஆல் வகுக்க,
5 x/5 = 190/5 = 38
x = 38
ஆகவே, சரியான விடை எழுதிய வினாக்களின் எண்ணிக்கை 38 ஆகும்.
எடுத்துக்காட்டு 3.14
60 மாணவர்களுடன் ஒரு பள்ளிப்பேருந்து புறப்பட்டது. முதல் நிறுத்தத்தில் சில மாணவர்கள் இறங்கினார்கள். இரண்டாம் நிறுத்தத்தில், முதல் நிறுத்தத்தில் இறங்கிய மாணவர்களின் எண்ணிக்கையைப் போல இரு மடங்கு மாணவர்கள் இறங்கினார்கள். மூன்றாம் நிறுத்தத்தில் 6 மாணவர்கள் இறங்கிய பிறகு, பேருந்தில் 3 மாணவர்கள் மட்டுமே இருந்தனர் எனில், முதல் நிறுத்தத்தில் இறங்கிய மாணவர்களின் எண்ணிக்கையைக் காண்க.
தீர்வு
முதல் நிறுத்தத்தில் இறங்கிய மாணவர்களின் எண்ணிக்கை நமக்குத் தெரியாததால், அந்த எண்ணை x என்க. எனவே, இரண்டாம் நிறுத்தத்தில் இறங்கியவர்களின் எண்ணிக்க 2 x ஆகும்.

ஆகவே , x + 2x +6+3 = 60
(1 + 2) x + 9 = 60
3x + 9 = 60
3 x + 9 –9 = 60 - 9 (இருபுறம் 9-ஐக் கழிக்க)
3 x = 51
3 x /3 = 51/ 3 (இருபுறமும் 3ஆல் வகுக்க)
ஆகவே, x = 17.
எனவே, முதல் நிறுத்தத்தில் இறங்கிய மாணவர் எண்ணிக்கை 17 ஆகும்.
எடுத்துக்காட்டு 3.15
ஒருமட்டைப்பந்து அணி (Cricket Team) கலந்துகொண்ட போட்டிகளில், தோற்றதை விட இரு ஆட்டங்கள் அதிகமாக வென்றார்கள். வெற்றிக்கு 5 புள்ளிகளும், தோல்விக்கு - 3 புள்ளிகளும் வழங்கப்படுகின்றன. அந்த அணி மொத்தத்தில் 50 புள்ளிகள் பெற்றிருந்தால், அந்த அணி கலந்துகொண்ட ஆட்டங்களின் எண்ணிக்கையைக் காண்க.
தீர்வு
இழந்த ஆட்டங்களின் எண்ணிக்கை = x என்க.
எனவே, வென்ற ஆட்டங்கள் = x + 2.
கொடுக்கப்பட்ட விவரங்களிலிருந்து, 5(x + 2) + ( - 3) x = 50
5 x + 10 – 3 x = 50
2 x + 10 = 50
2 x + 10 - 10 = 50 - 10 (இருபுறமும் 10ஐ கழிக்க)
2 x = 40
இருபுறமும் 2ஆல் வகுக்க, 2 x /2 = 40/2 எனவே, x = 20.
எனவே, மொத்த ஆட்டங்களின் எண்ணிக்கை
x + x + 2 = 2x+ 2
= (2 x 20) + 2
= 40 + 2
= 42.
இவற்றை முயல்க
கந்தனும், காவ்யாவும் நண்பர்கள். இருவரிடமும் சில பேனாக்கள் உள்ளன.
கந்தன்: நீ எனக்கு ஒரு பேனா தந்தால், நம் இருவரிடமும் சம எண்ணிக்கையில் பேனாக்கள் இருக்கும். தருவாயா?
காவ்யா : ஆனால், நீ உன்னிடம் உள்ள பேனாக்களில் இருந்து, எனக்கு ஒன்று தந்தால், உன்னிடம் இருப்பது போல், என்னிடம் இரு மடங்கு பேனாக்கள் இருக்கும். நீ தருவாயா?
இந்தச் சூழலுக்குப் பொருத்தமான இயற்கணிதச் சமன்பாடுகளை உருவாக்குக. இருவரிடமும் உள்ள பேனாக்களின் எண்ணிக்கையை ஊகிக்க முடிகிறதா?
கந்தனிடம் x பேனாக்கள் உள்ளன
காவ்யாவிடம் y
காவ்யா ஒரு பேனாவை கந்தனிடம் கொடுத்தால் இருவரிடமும் சம எண்ணிக்கையிலான பேனாக்கள்இருக்கும்
x + 1 = y – 1
x – y = – l – l
x – y = – 2 ………… (1)
கந்தன் ஒரு பேனாவை காவ்யாவிடம் கொடுத்தால் கந்தனைவிட காவியாவிடம் இருமடங்கு பேனாக்கள் இருக்கும்
y + l = 2(x – 1)
y + 1 = 2x – 2
2x – y = 1 + 2 = 3
2x – y = 3 …………. (2)
2x – y = 3
x – y = –2
கழிக்க – + +
x = 5
மாற்றாக x = 5in (1)
x – y = –2
5 – y = –2
–y = –2 –5 = –7
y =7
கந்தனிடம் 5 பேனாக்கள் உள்ளன
காவ்யாவிடம் 7 பேனாக்கள் உள்ளன