வடிவியல் | இரண்டாம் பருவம் அலகு 4 | 7ஆம் வகுப்பு கணக்கு - முக்கோணத்தின் கோணங்களின் கூடுதல் பண்பின் பயன்பாடு (Application of Angle Sum Property of Triangle) | 7th Maths : Term 2 Unit 4 : Geometry
7ஆம் வகுப்பு கணக்கு : இரண்டாம் பருவம் அலகு 4 : வடிவியல்
முக்கோணத்தின் கோணங்களின் கூடுதல் பண்பின் பயன்பாடு (Application of Angle Sum Property of Triangle)
முக்கோணத்தின் கோணங்களின் கூடுதல் பண்பின் பயன்பாடு (Application of Angle Sum Property of Triangle)
ஒரு முக்கோணத்தில் அமைந்துள்ள கோணங்களின் பண்புகளைக் குறித்து நாம் அறிந்துள்ளோம். அப்பண்புகளில் ஒன்று, முக்கோணத்திலுள்ள அனைத்துக் கோணங்களின் கூடுதல் 180° ஆகும். பின்வரும் செயல்பாட்டின் மூலம் இதை நாம் சரிபார்க்க இயலும்.
செயல்பாடு
ஏதேனும் ஒரு முக்கோணத்தை வரைந்து அதன் கோணங்களை வண்ணமிடுக. பின்வருமாறு பண்பினைச் சரிபார்க்க.
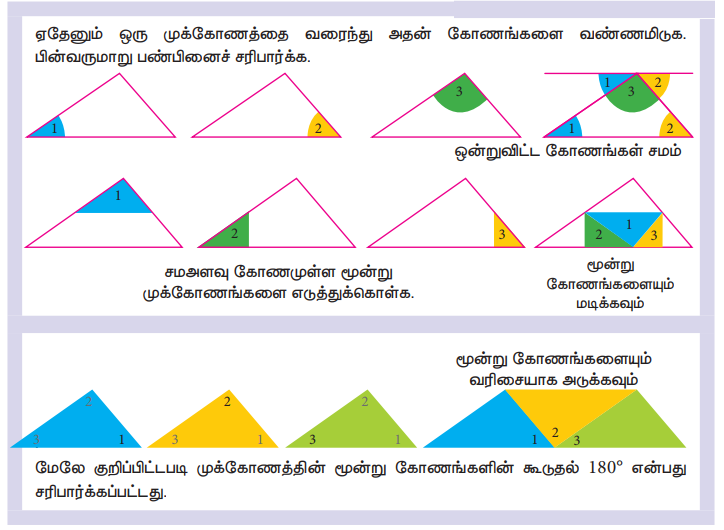
மேலே குறிப்பிட்டபடி முக்கோணத்தின் மூன்று கோணங்களின் கூடுதல் 180° என்பது சரிபார்க்கப்பட்டது.
இச்செயல்பாட்டிலிருந்து ஏதேனும் ஒரு முக்கோணத்தின் மூன்று கோணங்களின் கூடுதல் 180° என்ற முடிவு பெறப்பட்டுள்ளது.
இப்போது, இந்த முடிவை முறையாக நிரூபிப்போம்.
கொடுக்கப்பட்டது: முக்கோணம் ABC
∠A = x, ∠B = y மற்றும் ∠C= z எனக் கொள்க.
இப்போது நாம் x+y+z=180° என நிரூபிப்போம்.
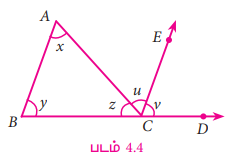
இதைச் செய்வதற்கு, BC ஐ D வரை நீட்டுவதும், CE என்ற கோட்டை C இலிருந்து AB இக்கு இணையாக வரைவதும் அவசியமாகும்.
CE ஆனது ∠ACE மற்றும் ∠ECD என்ற இரு கோணங்களை உருவாக்குகிறது. அவைகளை முறையே u மற்றும் v என எடுத்துக்கொள்வோம்.
இப்போது u, v, z ஆகியன ஒரு நேர்க்கோட்டின்மீது ஒரு புள்ளியில் அமையும் கோணங்களாகும்.
எனவே, z +u+v=180°. ... (1)
AB மற்றும் CE ஆகியன இணைகோடுகள், DB ஆனது ஒரு குறுக்குவெட்டி என்பதால்,
v = y (ஒத்த கோணங்கள்).
மேலும், AB மற்றும் CE ஆகியன இணைகோடுகள், AC ஆனது ஒரு குறுக்குவெட்டி என்பதால்,
u = x (ஒன்றுவிட்ட கோணங்கள்). மேலும் z+u+v= 180° [சமன்பாடு (1)]
இதில் u விற்கு மாற்றாக x ஐயும் v இக்கு மாற்றாக y உம் பதிலீடு செய்ய நமக்கு x+y+z=180° எனக் கிடைக்கிறது.
எனவே, ஒரு முக்கோணத்திலுள்ள அனைத்துக் கோணங்களின் கூடுதல் 180° ஆகும்.
எடுத்துக்காட்டு 4.1
கீழே கொடுக்கப்பட்டுள்ள கோணங்களைக் கொண்டு முக்கோணம் அமைக்க இயலுமா?
(i) 80°, 70°, 50°
(ii) 56°, 64°, 60°
தீர்வு
(i) கொடுக்கப்பட்ட கோணங்கள் 80°, 70°, 50°
கோணங்களின் கூடுதல் = 80°+70° + 50° = 200° ≠ 180°
எனவே, கொடுக்கப்பட்ட கோணங்களைக் கொண்டு முக்கோணம் அமைக்க இயலாது.
(ii) கொடுக்கப்பட்ட கோணங்கள் 56°, 64°, 60°
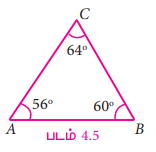
கோணங்களின் கூடுதல் = 56° + 64° + 60° = 180°
எனவே, கொடுக்கப்பட்ட கோணங்களைக் கொண்டு முக்கோணம் அமைக்க இயலும்.
எடுத்துக்காட்டு 4.2
கொடுக்கபட்டுள்ள ∆ABC இல் விடுபட்டக் கோண அளவைக் காண்க.
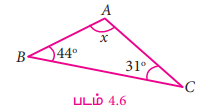
தீர்வு
∠A = x என்க.
∠A + ∠B + ∠C = 180° என நமக்குத் தெரியும். (முக்காணத்தில் கோணங்களின் கூடுதல் பண்பு)
x + 44° + 31° = 180°
x + 75° = 180°
x = 180°-75o
x = 105°
எடுத்துக்காட்டு 4.3
∆STU இல் SU = UT, ∠SUT = 70°, ∠STU = x எனில், x இன் மதிப்பைக் காண்க.
தீர்வு
கொடுக்கப்பட்டது ∠SUT = 70°
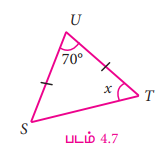
∠UST = ∠STU = x (சம பக்கங்களுக்கு எதிரேயுள்ள கோணங்கள்)
∠SUT + ∠UST + ∠STU = 180°
70° + x + x = 180°
70° + 2x = 180°
2x = 180°- 70o
2x = 110°
x = 110o/2 = 55o
எடுத்துக்காட்டு 4.4
ஒரு முக்கோணத்தில் இரண்டு கோணங்களின் அளவுகள் 65o மற்றும் 35° எனில், மூன்றாவது கோணத்தின் அளவைக் காண்க.
தீர்வு
கொடுக்கப்பட்ட கோணங்கள் 65° மற்றும் 35°.
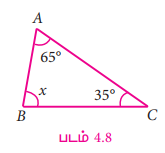
மூன்றாவது கோணத்தை x எனக் கொள்க.
65° + 35°+ x = 180°
100° + x = 180°
x = 180°-100o
x = 80o