வடிவியல் | இரண்டாம் பருவம் அலகு 4 | 7ஆம் வகுப்பு கணக்கு - வெளிக்கோணங்கள் (Exterior Angles) | 7th Maths : Term 2 Unit 4 : Geometry
7ஆம் வகுப்பு கணக்கு : இரண்டாம் பருவம் அலகு 4 : வடிவியல்
வெளிக்கோணங்கள் (Exterior Angles)
வெளிக்கோணங்கள் (Exterior Angles)
ஒரு முக்கோணத்தில் மூன்று முனைகள், மூன்று பக்கங்கள், மூன்று கோணங்கள் ஆகியன உள்ளன என நாம் அறிவோம். இப்போது, படம் 4.9 இல் கொடுக்கப்பட்டுள்ள முக்கோணத்தை உற்று நோக்குக.

∆ABC இல் பக்கம் AB ஆனது D வரை நீட்டிக்கப்பட்டுள்ளது. ∠CBD என்ற கோணத்தை உற்று நோக்குக. அக்கோணமானது BC மற்றும் BD ஆல் அமைகிறது. ∠CBD ஆனது ∆ABC இக்கு B இல் அமைந்த வெளிக்கோணம் எனப்படும்.
கோணங்கள், ∠ABC மற்றும் ∠CBD ஆகியவை அடுத்துள்ள கோணங்களாகும். மேலும் அவை நேரிய கோண இணைகளாக அமைவதையும் நாம் காணலாம்.
மேலும், ∠CAB மற்றும் ∠ACB ஆகியவை ∠CBD இக்கு அடுத்தடுத்து அமையாத கோணங்களாகும். அவை ∠CBD இக்கு உள்ளெதிர்க் கோணங்கள் என அழைக்கப்படுகின்றன.
சிந்திக்க
BC ஐ F வரை நீட்டினால், ∆ABC க்கு B இல் வெளிக் கோணம் அமையுமா?
குறிப்பு
∆ABC இல் பக்கங்கள் BC ஐ E வரையும், CA ஐ F வரையும் நீட்டிப்பதன் மூலம், C மற்றும் A இல் வெளிக்கோணங்களை அமைக்கலாம்.
முக்கோணத்தின் வெளிக்கோணங்களின் பண்புகள் (Exterior Angle Properties of a Triangle)
செயல்பாடு
முக்கோணத்தின் வெளிக்கோணங்களின் பண்புகளைப் புரிந்துகொள்ளக் கீழே கொடுக்கப்பட்டுள்ள முக்கோணங்களின் வெளிக்கோணங்களைப் பட்டியலிடுக.
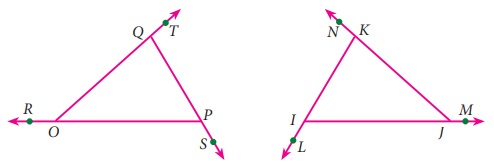
ஒவ்வொரு வெளிக்கோணத்தையும் அவற்றின் உள்ளெதிர்க் கோணங்களையும் அளந்து அட்டவணைப்படுத்துக. இம்முடிவை முறையாக நிரூபிக்க முயற்சி செய்வோம்
மேலே உள்ள செயல்பாட்டிலிருந்து ஒரு முக்கோணத்தின் வெளிக்கோணமானது அதன் உள்ளெதிர்க் கோணங்களின் கூடுதலுக்குச் சமம் என்றறிகிறோம்.
நிரூபணம் :
∆ABC இல் A, B மற்றும் C இல் அமையும் கோணங்களை முறையே a, b மற்றும் C எனவும், A, B மற்றும் C இல் அமையும் வெளிக்கோணங்களை x, y மற்றும் z எனவும் எடுத்துக்கொள்வோம்.
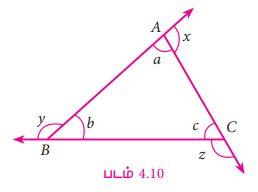
x= b+c, y = a+c மற்றும் z = a+b என நிரூபிக்க வேண்டும்.
a + x = 180° (நேரிய கோண இணைகள் மிகை நிரப்பிகள்)
இதிலிருந்து, x = 180° - a ... (1)
இப்போது, a + b + c = 180° (முக்கோணத்தின் மூன்று கோணங்களின் கூடுதல் 180° )
இதிலிருந்து, b + c = 180° - a ...(2)
(1) மற்றும் (2) சமன்பாடுகளிலிருந்து, x மற்றும் b+c இரண்டும் சமமாக உள்ளது.
எனவே , x = b+c.
செயல்பாடு
முக்கோணத்தின் ஒரு முனையில் ஒருவர் நின்று கொண்டிருப்பதாகக் கொள்வோம். அவர் முக்கோணத்தின் பக்கங்கள் வழியாகத் தொடக்கப்புள்ளியை அடையும் வரை நடப்பதாகக் கொள்வோம். ஒவ்வொரு முனையிலும், அம்முனையில் அமைந்த வெளிக்கோணத்திற்கு சம அளவில் திரும்புவார். எனவே முக்கோணத்தைச் சுற்றி முழுமையான பயணத்திற்குப் பிறகு ஒரு முழுச் சுற்றுக் கோணமான 360° கோண அளவிற்குத் திரும்பியிருப்பார்.
இம்முடிவைப் பின்வருமாறு நிரூபிப்போம்.
ஒரு நேர்கோட்டின் மீது அமையும் கோணம் 180° , என்பதால்,
a + x = 180° [நேரியக் கோண இணைகள் மிகை நிரப்பிகள்]
x = 180° - a
இதேபோன்று, y = 180° -b
மேலும் z = 180° - c
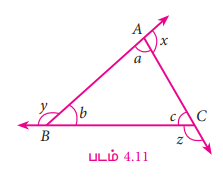
எனவே, x + y + z = (180° - a) + (180° - b) + (180° - c)
= 540 – (a + b + c)
= 540°-180° [ஒரு முக்கோணத்தின் மூன்று கோணங்களின் கூடுதல் 180°]
= 360°
எனவே, முக்கோணத்தின் அனைத்து வெளிக்கோணங்களின் கூடுதல் 360° ஆகும்.
மேற்கண்டவைகளில் இருந்து வெளிக்கோணத்தின் இரண்டு முக்கியமான பண்புகளைப் பெறுகிறோம்.
(i) ஒரு முக்கோணத்தின், ஒரு வெளிக்கோணமானது இரண்டு உள்ளெதிர்க் கோணங்களின் கூடுதலுக்குச் சமம்.
(ii) ஒரு முக்கோணத்தில் மூன்று வெளிக்கோணங்களின் கூடுதல் 360°.
எடுத்துக்காட்டு 4.5
∆PQR, R இல் அமையும் ∠SRQ என்ற வெளிக்கோணத்தைக் கண்டுபிடி.
தீர்வு
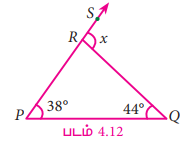
வெளிக்கோணம் = இரு உள்ளெதிர்க் கோணங்களின் கூடுதல்
x = 38° + 44° = 82°
எடுத்துக்காட்டு 4.6
∆LMN இல் LM ஆனது O வரை நீட்டிக்கப்பட்டுள்ளது.
∠L = 62° மற்றும் ∠N = 31° எனில், ∠NMO ஐக் காண்க.
தீர்வு
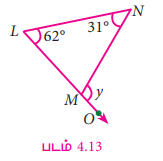
∠NMO = y என்க.
வெளிக்கோணம் = இரு உள்ளெதிர்க் கோணங்களின் கூடுதல்
y = 62° +31o
= 93°
எடுத்துக்காட்டு 4.7
படத்தில் கொடுக்கப்பட்டுள்ள ∆ABC இல் z இன் மதிப்பு காண்க.
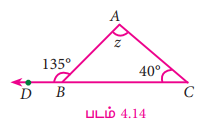
தீர்வு
வெளிக்கோணம் = இரு உள்ளெதிர்க் கோணங்களின் கூடுதல்
135° = z +40°
இருபுறமும் 40° ஐக் கழிக்க.
135° - 40° = z +40° - 40°
z = 95o
எடுத்துக்காட்டு 4.8
படத்தில் கொடுக்கப்பட்டுள்ள இருசமபக்க முக்கோணம் ∆IJK இல் ∠IKL =128° எனில், x இன் மதிப்பைக் காண்க.
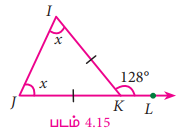
தீர்வு
வெளிக்கோணம் = இரு உள்ளெதிர்க் கோணங்களின் கூடுதல்
128° = x + x
128 = 2x
128/2=2x/2 [இருபுறமும் 2 ஆல் வகுக்க.)
x = 64°
எடுத்துக்காட்டு 4.9
படம் 4.16 இல் கொடுக்கப்பட்டுள்ள விவரங்களிலிருந்து ∠UWY இன் மதிப்பைக் காண்க. ∠XWV பற்றி நீங்கள் என்ன கருதுகிறீர்கள்?
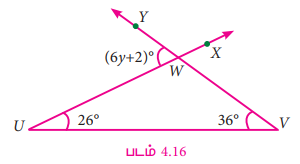
தீர்வு
வெளிக்கோணம் = இரு உள்ளெதிர்க் கோணங்களின் கூடுதல்
6y+2 = 26° +36o
6y+2 = 62°
இருபுறமும் 2 ஐக் கழிக்க,
6y = 62-2
6y = 60°
6y/6 = 60/6 [இருபுறமும் 6ஆல் வகுக்க]
y =10° ஆகவே,
∠UWY = 6y + 2 = 6(10) + 2 = 62°.
மேலும், ∠XWV = ∠UWY, ஏனெனில் இவ்விரு வெளிக்காணங்களும் குத்தெதிர்க் கோணங்கள் ஆகும்.